| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- XGBoost
- sql
- 데이터 증식
- DENSE_RANK()
- ARIMA
- 데이터 핸들링
- Growth hacking
- WITH ROLLUP
- 그룹 연산
- lightgbm
- 컨브넷
- 부트 스트래핑
- 3기가 마지막이라니..!
- 스태킹 앙상블
- ImageDateGenerator
- python
- 그로스 마케팅
- 데이터 정합성
- 캐글 신용카드 사기 검출
- splitlines
- 마케팅 보다는 취준 강연 같다(?)
- WITH CUBE
- 로그 변환
- 그로스 해킹
- 캐글 산탄데르 고객 만족 예측
- 인프런
- pmdarima
- 리프 중심 트리 분할
- 분석 패널
- tableau
- Today
- Total
LITTLE BY LITTLE
[9-2] 실무로 통하는 인과추론 with 파이썬 - 9장. 통제집단합성법 본문

목차
<9장. 통제집단합성법(Synthetic Control Method)>
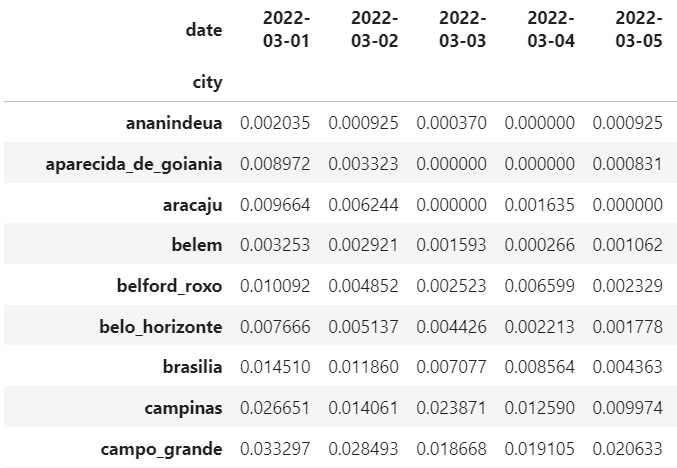
9.1 온라인 마케팅 데이터셋
9.2 행렬 표현
9.3 통제집단합성법과 수평 회귀분석
9.4 표준 통제집단합성법
9.5 통제집단합성법과 공변량
9.6 통제집단합성법과 편향 제거
9.7 추론
9.8 합성 이중차분법
9.8.1 이중차분법 복습
9.8.2 통제집단합성법 복습
9.8.3 시간 가중치 추정하기
9.8.4 통제집단합성법과 이중차분법
9.9 요약
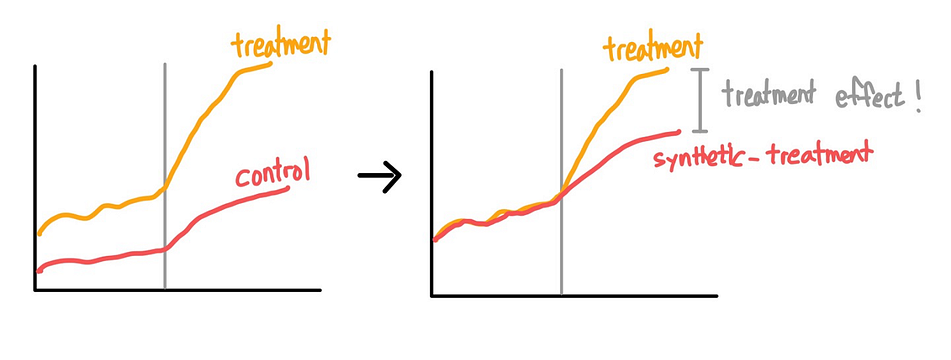
9.5 통제집단합성법과 공변량
- 일반적으로 우리는 대조군의 처치 전 결과를 특성으로 Ytr 을 예측한다.
- 드물긴 하지만, 만약 예측력이 좋다고 생각되는 공변량이 있다면, 포함시킬 수 있다.
시장 규모에 따라 정규화한 경쟁사의 일별 다운로드 수 데이터(comp_download_pct)를 공변량으로 모델에 포함시켜보자.
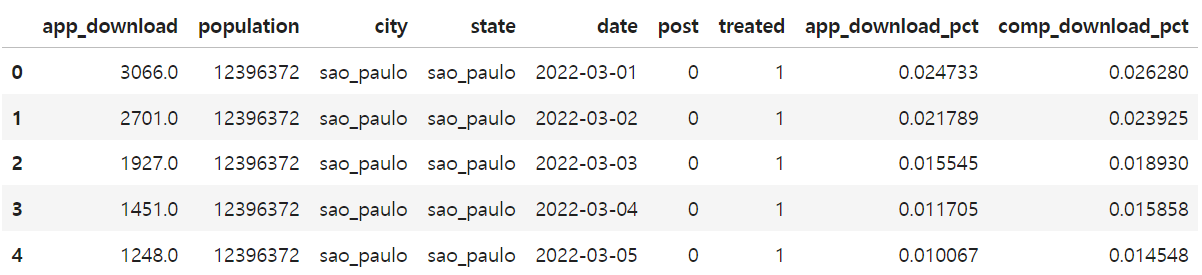
- 가중치 wi가 yco 뿐만 아니라, 추가 공변량인 xco에도 곱해져 Ytr을 잘 근사할 수 있도록 가상의 대조군을 구성하고자함
하지만 yco와 xco의 척도가 다르거나, 예측력이 다를 수 있기에, 척도 인자(scaling factor) ν 를 곱해야 한다.
- 공변량 X의 관점으로 yco를 또다른 공변량을 취급
- 척도 인자를 곱해서 목적 함수를 재구성하면,

위의 목적함수에서 최적의 ν를 찾기 위해서는 전체 통제집단 합성법을 또다른 최적화 목적함수로 묶어야 한다.
1. reshaper를 정의하여 reshape_sc_data 함수 생성 시 필요한 몇 가지 인자를 미리 설정
- partial() : 함수의 특정 인자를 항상 특정 값으로 고정해서 사용하고자 할 때 사용
from toolz import partial
reshaper = partial(reshape_sc_data,
df=df_norm_cov,
geo_col="city",
time_col="date",
tr_geos=treated,
tr_start=str(tr_period))
2. reshaper 함수를 사용하여 app_download_pct 열 기준 데이터 변형
y_pre_co, y_pre_tr, y_post_co, y_post_tr = reshaper(
y_col="app_download_pct")

x_pre_co, _, x_post_co, _ = reshaper(y_col="comp_download_pct")
3. 가중치 찾기
- X_times_v : x_co_list와 vs(척도인자)의 요소를 쌍으로 묶어 각각의 곱을 계산하고 합산하여 X_times_v에 할당
- SyntheticControl 모델 객체 생성, X_times_v와 y_tr_pre로 모델 학습
- return: 학습 결과 손실(loss_)과 가중치(w_) 딕셔너리 반환
def find_w_given_vs(vs, x_co_list, y_tr_pre):
X_times_v = sum([x*v for x, v in zip(x_co_list, vs)])
model = SyntheticControl()
model.fit(X_times_v, y_tr_pre)
return {"loss": model.loss_, "w": model.w_}
4. 배열 v를 인수로 받아 minimize 함수로 최적화 손실을 반환하는 함수 생성
from scipy.optimize import minimize
def v_loss(vs):
return find_w_given_vs(vs,
[y_pre_co, x_pre_co],
y_pre_tr.mean(axis=1)).get("loss")
v_solution = minimize(v_loss, [0, 0], method='L-BFGS-B')
v_solution.x[Out]
array([1.88034589, 0.00269853])
5. 도출된 최적의 척도인자 ν를 활용하여 공변량을 고려한 가상의 대조군 가중치 얻기
*[y_pre_co, x_pre_co]의 ν 가 각각 1.88, 0.002로, 크기가 작아 공변량을 고려하지 않았을 때의 결과와 유사할 것
w_cov = find_w_given_vs(v_solution.x,
[y_pre_co, x_pre_co],
y_pre_tr.mean(axis=1)).get("w").round(3)
w_covarray([-0. , -0. , 0. , -0. , -0. , -0. , 0.078, 0.001,
0.033, 0. , -0. , 0.034, -0. , -0. , -0. , 0. ,
0.016, 0.047, 0.03 , 0.01 , -0. , -0. , 0. , 0.055,
-0. , 0. , -0. , 0. , 0. , 0. , -0. , 0.046,
0.078, 0.007, 0. , 0. , 0.138, 0. , 0.022, 0.008,
-0. , 0.201, 0. , 0.035, 0. , 0.161, -0. ])
6. 가중치를 사용해서 Y(0)에 대해 예측하고, 최종 ATT 추정
y0_hat = sum([x*v for x, v
in zip([y_post_co, x_post_co], v_solution.x)]).dot(w_cov)
att = y_post_tr.mean(axis=1) - y0_hatplt.figure(figsize=(10,4))
plt.plot(y_co.index, y_tr.mean(axis=1) - model.predict(y_co), label="공변량 포함X ", ls="-.")
plt.plot(att.index, att, label="공변량 포함O")
plt.hlines(0, y_co.index.min(), y_co.index.max())
plt.vlines(pd.to_datetime("2022-05-01"), -0.01, 0.015)
plt.legend()
plt.ylabel("ATT")
plt.xticks(rotation=45);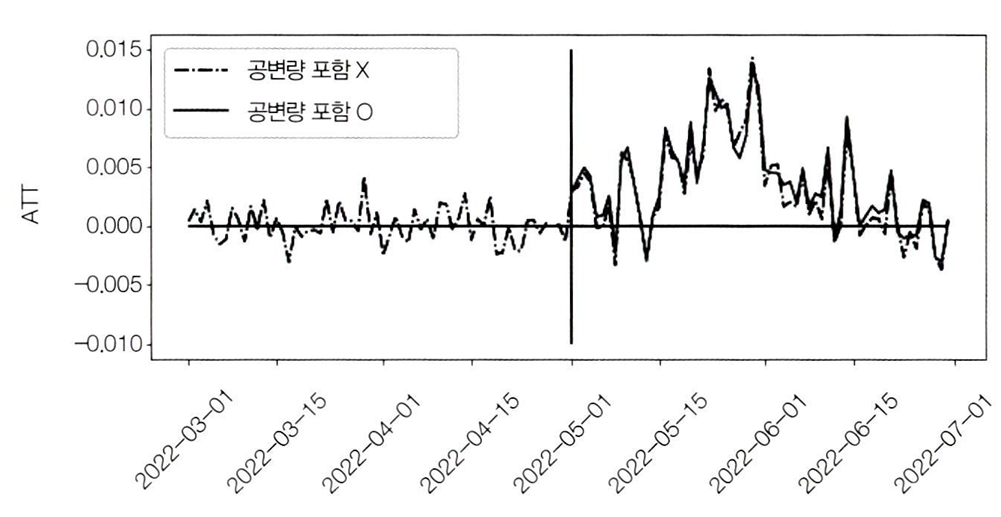
9.6 통제집단합성법과 편향제거
통제집단합성법의 예측 방은 머신러닝 모델과 마찬가지로, Tpre의 수가 적으면, 과적합이 발생하기 쉽다.
통제집단합성법의 편향을 이해하기 위해 ATT 개입 이후 기간의 시간별 평균으로 재정의하면,
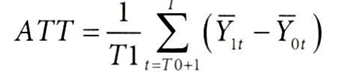
- T1 : 사후 기간(post-treatment period)의 길이로 나누어 사후 기간 동안의 평균을 계산
- ∑t=T0+1: 개입 이후~ (= T0은 개입 이전의 마지막 시점 )
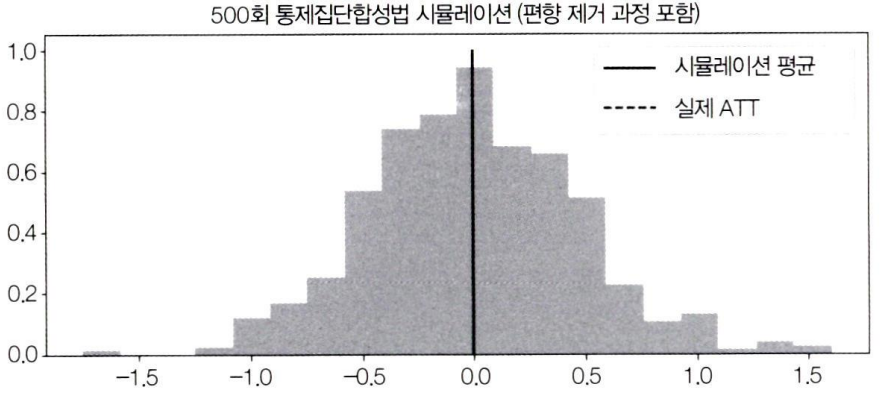
Synthetic Control 방법을 사용하여 500번의 시뮬레이션을 수행하고, 그 결과를 히스토그램으로 시각화

이중/편향 제거 머신러닝( 7장 )에서 배운 과적합 편향을 해결하는 교차 예측 검증(cross_fitting)을 실행해보자.
세 단계로 구성
- 개입 전 기간을 k개의 블록으로 나누고, 크기를 min(Tre/k, Tpost)로 설정한다.
- 각 블록을 hold-out set으로 취급하고, 1/Y^k,pre,co와 1/Y^k,tr에 대한 통제집단합성법 모델을 적합시킨다.
- ^-k는 train set에서 블록을 삭제한다는 의미
- 이 단계에서 w^-k의 가중치를 준다.
- 홀드아웃 데이터 Y^k pre,co를 사용하여 2번의 가중치로 표본 외 예측을 한다.
- 홀드아웃 데이터에서 예측값과 관측값 사이의 평균 차이가 편향에 대한 추정값
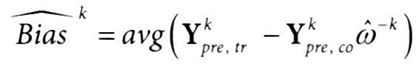
개입 전 기간 5개, 개입 후 기간 3개, k=2 블록을 구성한다고 가정해보면,
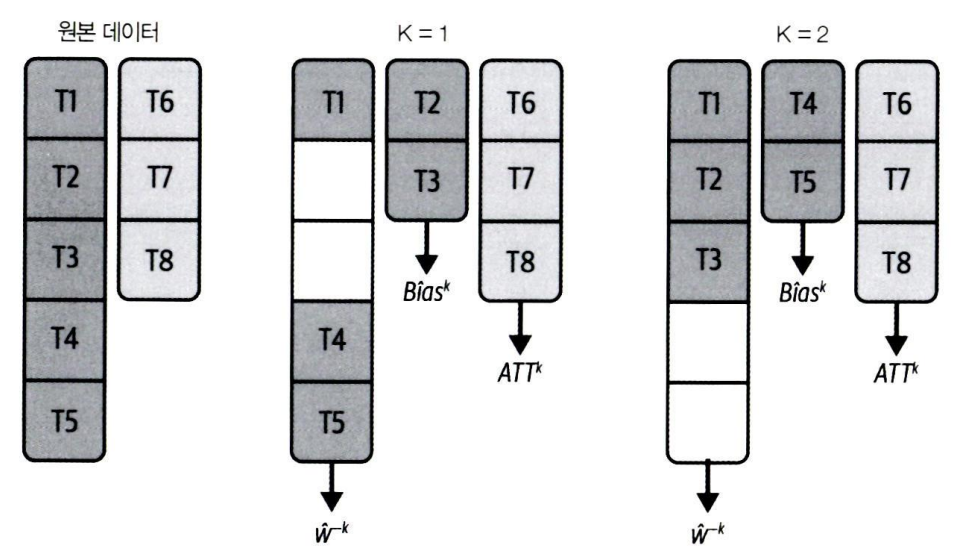
- 블록크기 = min(Tre/k, Tpost) = min(5/2, 3) = 2.5라서 2로 버림
- 블록 2개가 제외된 훈련 데이터셋으로 통제집단합성법 모델을 추정하여 w^-k 얻기 & 제외된 블록2개에서 편향 추정
- 2에서 구한 가중치(w^-k)와 편향(bias^k)를 모두 활용해서 개입 후 기간의 ATT 추정
코드로 구현해보자.
1. min(Tre/k, Tpost) : y_pre_tr을 K로 나누고, 개입 후 기간 길이와 비교하여 최소 값을 선택
def debiased_sc_atts(y_pre_co, y_pre_tr, y_post_co, y_post_tr, K=3):
block_size = int(min(np.floor(len(y_pre_tr)/K), len(y_post_tr)))
2. np.split으로 인덱스를 K개 블록으로 나누기
blocks = np.split(y_pre_tr.index[-K*block_size:], K)
3. SyntheticControl 모델을 초기화하고, hold_out 블록을 제외한 데이터를 사용하여 모델을 학습
def fold_effect(hold_out):
model = SyntheticControl()
model.fit(
y_pre_co.drop(hold_out),
y_pre_tr.drop(hold_out))
4. bias_hat: 검증용 데이터에서 예측된 값과 실제 값의 차이의 평균으로 편향을 추정
bias_hat = np.mean(y_pre_tr.loc[hold_out]
- model.predict(y_pre_co.loc[hold_out]))
5. y0_hat: 처리 후 대조군 데이터를 사용하여 예측된 처리군 결과로 (y_post_tr - y0_hat) - bias_hat를 계산하여, 편향을 제거한 값을 반환
y0_hat = model.predict(y_post_co)
return (y_post_tr - y0_hat) - bias_hat
return pd.DataFrame([fold_effect(block) for block in blocks]).Tdeb_atts = debiased_sc_atts(y_pre_co,
y_pre_tr.mean(axis=1),
y_post_co,
y_post_tr.mean(axis=1),
K=3)
deb_atts.head()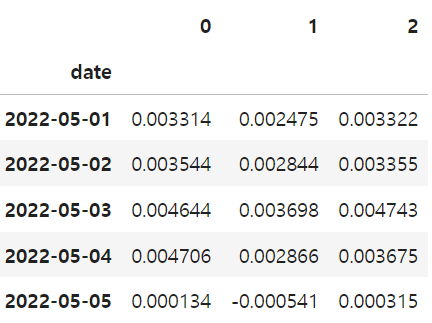
편향된 ATT 계산하여 비교해보기
model_biased = SyntheticControl()
model_biased.fit(y_pre_co, y_pre_tr.mean(axis=1))
att_biased = y_post_tr.mean(axis=1) - model_biased.predict(y_post_co)
편향 제거된 ATT의 분포는 원래대로 평균이 0이 됨(▼)
9.7 추론
- 교차 예측 검증을 통해서 편향을 제거하는 과정은 ATT 추정값 주위에 신뢰구간을 설정할 때에도 활용되어 중요하다.
- 통제집단합성법을 활용하여 추론하는 것은 꽤 까다롭다.
- 8장에서 이중 강건 이중차분법(8.6)에서 부트스트랩을 통해서 신뢰구간을 구했던 방법을 통제집단합성법에 적용할 수 없다.
- 가상의 대조군을 구성하기에 대조군이 적거나, 심지어 하나일 때 사용하는 방법이 통제집단합성법이다 보니, 많은 부트스트랩 표본이 모든 실험군을 제외해서 ATT가 정의되지 않기 때문
→ 부트스트랩 대신 시간 차원을 순열하는 방법으로 추론하는 방법이 제안됨
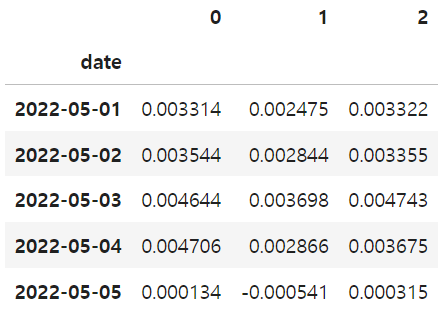
debiased_sc_atts() 함수 실행 결과로 도출된 블록(0,1,2)별 날짜별 ATT의 추정값에 대한 신뢰구간을 구해보자.
atts_k = deb_atts.mean(axis=0).values # 각 블록에서의 평균 ATT
att = np.mean(atts_k) # 전체 평균 ATT
print("atts_k:", atts_k)
print("ATT:", att)[Out]
atts_k: [0.00414872 0.00260513 0.00322101]
ATT: 0.003324950193632595
위의 수식 구현 - 표준오차 SE 계산
K = len(atts_k) # 블록 개수
T0 = len(y_pre_co) # 개입 전 기간 길이
T1 = len(y_post_co) # 개입 후 기간 길이
block_size = min(np.floor(T0/K), T1) # 개입 전 기간 / 블록 수 or 개입 후 기간 중 MIN 사용
se_hat=np.sqrt(1+((K*block_size)/T1))*np.std(atts_k, ddof=1)/np.sqrt(K) # ddof=1 -> 자유도=1 (표본표준편차이기 때문에 자유도를 1로 설정)
print("SE:", se_hat)[Out]
SE: 0.0006318346108228888
구한 표준오차를 사용해서 H0:ATT=0 하에서 자유도가 K-1인 점근 T분포를 갖는 검정통계량 ATT/SE 구하기
T분포로 α=0.1인 90% 신뢰구간 구하기
from scipy.stats import t
alpha = 0.1
[att - t.ppf(1-alpha/2, K-1)*se_hat,
att + t.ppf(1-alpha/2, K-1)*se_hat][Out]
[0.0014800022408602205, 0.005169898146404969]- 사용한 표준오차 공식에서 K값을 크게 하면 신뢰구간이 좁아진다.
- 하지만, 좁은 신뢰구간에서는 더 낮은 확률로 실제 ATT를 포함하게 된다.
- 위 방법은 기간별 추론에는 사용할 수 없다. (이 방법으로 시간에 따른 처치효과의 신뢰구간은 구할 수 없음)
- 이론 상 T0(개입 전 기간의 길이)와 T1(개입 후 기간의 길이)가 모두 커야하기 때문
9.8 합성 이중차분법
톻제집단합성법(SC)이 이중차분법(DID)가 어떻게 연관되는지에 대한 새로운 관점
- 두 방법을 하나의 합성 이중차분법(SDID, Synthetic Difference-In-Difference) 추정량으로 결합하는 방법\
9.8.1 이중차분법 복습
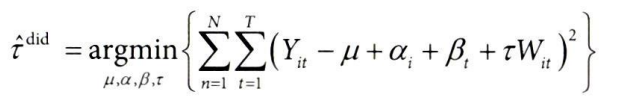
* τ = ATT
* αi: 대상 고정효과 = 실험 대상의 절편 차이
* βt: 시간 고정효과 = 실험군-대조군 모두에 걸친 일반적인 추세
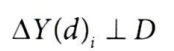
- 이중차분법의 기본 가정 : 특정 시점에서의 처치로 인한 결과의 변화 (△Y(d)i)가 처치 변수(D)와 독립적이어야 함
- 즉, 처치가 주어졌는지 여부에 관계 없이 결과 Y의 변화가 무작위적으로 분포
9.8.2 통제집단합성법 복습
통제집단합성법 추정량을 이중차분법 식처럼 재구성해보면, 다음과 같이 최적화 문제를 푸는 식으로 작성할 수 있다.

*Wit: 시간 t에서 단위 i가 처치 받았는지 여부
*wi^sc: 통제집단합성법의 목적함수를 최적화하여 얻는 가중치
이중차분법과의 차이점
| 항목 | 통제집단합성법(SC) | 이중차분법(DID) |
| 최적화 변수 | β, τ | μ, α, β,τ |
| 시간 고정 효과 βt | O | O |
| 단위 고정 효과 αi | X | O |
| 전체 평균 효과 μ | X | O |
| 가중치 ωi ^sc | O | X |
- 모두 시간 고정효과(βt)는 포함하지만, 이중차분법은 단위 고정 효과(αi)가 모두 동일하여 전체 평균효과(μ) 를 갖는 반면, 통제집단합성법은 단위 각각이 가중치(ωi ^sc)를 가짐
- 합성 이중차분법은 두 가지 요소를 모두 포함해서 합치는 방법
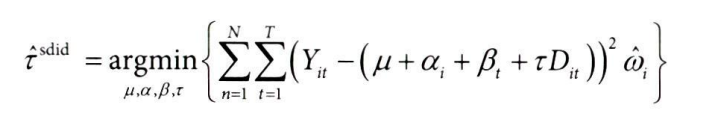
통제집단합성법을 추정하고 ATT를 계산해보자
1. 가상의 대조군 가중치 생성
sc_model = SyntheticControl()
sc_model.fit(y_pre_co, y_pre_tr.mean(axis=1))
(y_post_tr.mean(axis=1) - sc_model.predict(y_post_co)).mean()[Out]
0.003327040979396121
2. 행렬을 재구성하기 전, 각 대조군 도시에 가중치 w를 매핑하여 실험 대상 가중치(unit_weight) df 생성하기
unit_w = pd.DataFrame(zip(y_pre_co.columns, sc_model.w_),
columns=["city", "unit_weight"])
unit_w.head()
3. 생성한 가중치(unit_weight) df를 원래의 df에 조인
- post * treated의 곱으로 tr_post 생성 (W = Di*Postt)
- 도시 기준 left join하여 도시별 가중치 추가
- NaN 값을 treated 컬럼의 평균값으로 채우기
df_with_w = (df_norm
.assign(tr_post = lambda d: d["post"]*d["treated"])
.merge(unit_w, on=["city"], how="left")
.fillna({"unit_weight": df_norm["treated"].mean()}))
df_with_w.head()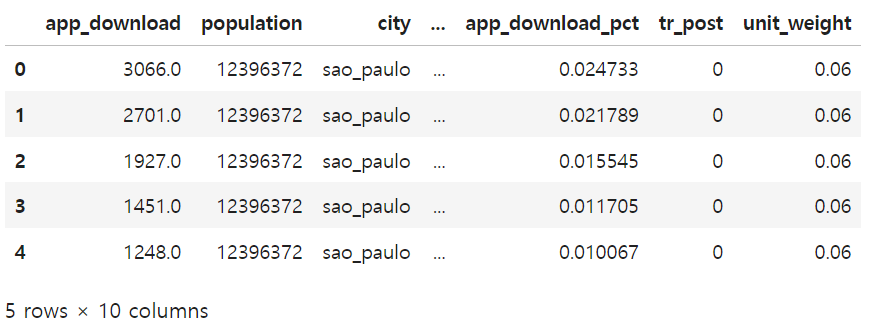
4. 공식을 따라 시간 고정 효과(βt)가 있는 가중 OLS 활용하기
- wls(Weighted Least Squares) 함수 사용
- C(date) : 날짜 고정 효과 포함
- query로 필터링하여 unit_weight가 매우 작은 가중치 제외
- 가중치를 unit_weight값으로 설정
mod = smf.wls(
"app_download_pct ~ tr_post + C(date)",
data=df_with_w.query("unit_weight>=1e-10"),
weights=df_with_w.query("unit_weight>=1e-10")["unit_weight"]
)
mod.fit().params["tr_post"][Out]
0.0033293800074678703
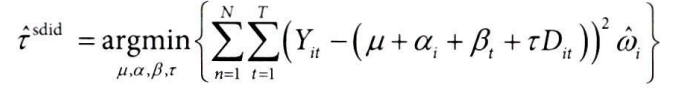
- 가중치를 실험 대상에만 주는 이유는, 목적이 대조군을 사용하여 실험군과 비슷하게 만들기 위하는 것이기 때문이다.
- 처치 전 기간의 가중치 (시간 가중치)를 사용하여 처치 후 기간을 더 잘 근사할 수도 있다.
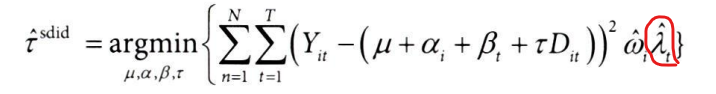
다음으로 시간 가중치를 추정하는 방법에 대해 알아보자.
9.8.3 시간 가중치 추정하기
앞서 실험대상 가중치(wi^sc)를 구한 식

→ 처치 전 실험군 평균 결과(Ypre,tr)를 대조군 결과에 회귀
시간 가중치를 구하는 식으로 변환하면,
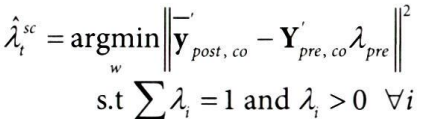
위 식에서
- Ypre,co를 전치(Y'pre,co)해서
- 처치 후 대조군 평균 결과(Ypost,co)에 회귀하면 시간 가중치를 구할 수 있다.

- 평균 처치 후 기간이 처치 전 기간보다 낮은 결과를 보일 경우, 외삽이 필요할 수 있다.
- 통제집단합성법은 외삽을 허용하지 않는 대신 절편 이동(+λ0)을 허용한다.
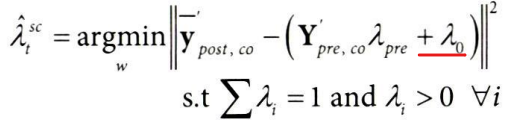
코드로 확인해보자.
from sklearn.base import BaseEstimator, RegressorMixin
from sklearn.utils.validation import check_X_y, check_array, check_is_fitted
import cvxpy as cp
class SyntheticControl(BaseEstimator, RegressorMixin):
def __init__(self, fit_intercept=False):
self.fit_intercept = fit_intercept
def fit(self, y_pre_co, y_pre_tr):
y_pre_co, y_pre_tr = check_X_y(y_pre_co, y_pre_tr)
fit_intercept 파라미터를 사용해서 절편을 적합시킴
- intercept : True*1=1이라는 사실을 활용해서 true인 경우 모든 값이 1인 열을 추가
- X: intercept가 추가된 대조군 데이터 정의
# 절편 추가
intercept = np.ones((y_pre_co.shape[0], 1))*self.fit_intercept
X = np.concatenate([intercept, y_pre_co], axis=1)
w = cp.Variable(X.shape[1])
목적 함수&제약 조건 정의, 최적화 후 가중치 구하기
objective = cp.Minimize(cp.sum_squares(X@w - y_pre_tr))
constraints = [cp.sum(w[1:]) == 1, w[1:] >= 0]
problem = cp.Problem(objective, constraints)
self.loss_ = problem.solve(verbose=False)
self.w_ = w.value[1:] # remove intercept
self.is_fitted_ = True
return self def predict(self, y_co):
check_is_fitted(self)
y_co = check_array(y_co)
return y_co @ self.w_
시간 가중치 추정하기
time_sc = SyntheticControl(fit_intercept=True)
time_sc.fit(
y_pre_co.T, # 전치
y_post_co.mean(axis=0) # 처치 후 대조군 평균 결과에 회귀
)
time_w = pd.DataFrame(zip(y_pre_co.index, time_sc.w_),
columns=["date", "time_weight"])
time_w.tail()
plt.figure(figsize=(10,4))
plt.bar(time_w["date"], time_w["time_weight"])
plt.ylabel("Time Weights")
plt.xticks(rotation=45);
9.8.4 통제집단합성법과 이중차분법
기존의 데이터프레임에 시간 가중치를 조인
- time_w에는 개입 전 기간의 가중치만 있으므로, 개입 후 시간 가중치를 post변수의 평균값으로 채우기
- 마지막으로 가중치 wi 와 λt를 모두 곱해서 최종 가중치 구하기
scdid_df = (
df_with_w
.merge(time_w, on=["date"], how="left")
.fillna({"time_weight":df_norm["post"].mean()})
.assign(weight = lambda d: (d["time_weight"]*d["unit_weight"]))
)
wls로 가중 회귀분석 수행
did_model = smf.wls(
"app_download_pct ~ treated*post",
data=scdid_df.query("weight>1e-10"),
weights=scdid_df.query("weight>1e-10")["weight"]).fit()
did_model.params["treated:post"][Out]
0.004086196404101931
실험군과 가상의 대조군으로 얻은 반사실 추세(점선) 시각화 (코드 생략)

아래 그래프를 보면, 합성 이중차분법이 개입 후 기간에 더 가까운 시간대를 활용하는 경향이 있는 것을 확인할 수 있다.
합성 이중차분법이 흥미로운 이유는,
- 추정량에 대한 통제집단합성법 구성 요소는 이중차분법의 평행 추세 가정을 더 설득력 있게 만듦
- 실험군을 모방하는 가상의 대조군을 만들면 평행 추세를 더 쉽게 얻을 수 있음
- 이중차분법과 통제집단합성법보다 편향이 더 낮음 (분산이 더 낮은 경향이 있기 때문)
하지만, 절편 이동을 하는 것에는 댓가가 따른다.
→ 가능한 가중치의 범위를 제한할 수 있는 볼록성 제약 조건이 제거된다. (∑ωi=1 & ωi>0 ∀i)
→ 가정에 더 유연하므로 좋다고 볼 수 있으나, 위험한 외삽을 허용하므로 그렇지 않다고 볼 수도 있음
'데이터 분석 > 인과추론' 카테고리의 다른 글
| [11] 실무로 통하는 인과추론 with 파이썬 - 11장. 불응과 도구변수 (0) | 2024.07.23 |
|---|---|
| [10] 실무로 통하는 인과추론 with 파이썬 - 10장. 지역 실험과 스위치백 실험 (0) | 2024.07.16 |
| [9-1] 실무로 통하는 인과추론 with 파이썬 - 9장. 통제집단합성법 (0) | 2024.06.23 |
| [8-2] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 (0) | 2024.06.16 |
| [8-1] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 (0) | 2024.06.11 |




