| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 그로스 마케팅
- 컨브넷
- 스태킹 앙상블
- 마케팅 보다는 취준 강연 같다(?)
- ImageDateGenerator
- ARIMA
- 로그 변환
- lightgbm
- Growth hacking
- DENSE_RANK()
- 캐글 산탄데르 고객 만족 예측
- 인프런
- XGBoost
- 그룹 연산
- 리프 중심 트리 분할
- sql
- 캐글 신용카드 사기 검출
- 분석 패널
- tableau
- 데이터 증식
- python
- WITH ROLLUP
- 그로스 해킹
- 3기가 마지막이라니..!
- 데이터 핸들링
- 데이터 정합성
- WITH CUBE
- splitlines
- pmdarima
- 부트 스트래핑
- Today
- Total
LITTLE BY LITTLE
[8-1] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 본문

목차
<8장 이중차분법>
8.1 패널데이터
8.2 표준 이중차분법
8.2.1 이중차분법과 결과 변화
8.2.2 이중차분법과 OLS
8.2.3 이중차분법과 고정효과
8.2.4 이중차분법과 블록 디자인
8.2.5 추론
8.3 식별 가정
8.3.1 평행 추세
8.3.2 비기대 가정과 SUTVA
8.3.3 강외생성
8.3.4 시간에 따라 변하지 않는 교란 요인
8.3.5 피드백 없음
8.3.6 이월 효과와 시차종속변수 없음
8.4 시간에 따른 효과 변동
8.5 이중차분법과 공변량
8.6 이중 강건 이중차분법
8.6.1 성향점수 모델
8.6.2 델타 결과 모델
8.6.3 최종 결과
8.7 처치의 시차 도입
8.7.1 시간에 따른 이질적 효과
8.7.2 공변량
8.8 요약
8장. 이중차분법

- 다시 ATE 추정으로 돌아가서, 인과추론에 패널데이터를 활용하는 방법에 대해 배운다.
- 패널 데이터
- 시간에 따라 반복해서 관측되는 데이터
- 동일한 실험 대상을 여러 시간대에 걸쳐 관측하면 동일한 대상에 처치 전/후에 무슨 일이 일어나는지 알 수 있다.
- 랜덤화가 불가능할 때 인과효과를 식별할 수 있는 좋은 대안이 될 수 있음
- 관측 데이터를 갖고 있고, 관측되지 않는 교란 요인이 존재할 가능성이 높을 때 패널데이터 방법이 효과적일 것
- 인과추론에서 패널데이터가 중요한 이유를 살펴보고, 이중차분법과 다양한 변형 기법에 대해 배운다.
✅ 데이터 구조
횡단면 데이터
- 패널 데이터나 종단(longitudinal) 설계와 달리, 각 실험 대상이 한 번만 나타나는 데이터
- 그 사이에 속하는 '반복 횡단면 데이터'도 있는데, 이 유형은 여러 실험 대상을 여러 시간대에 걸쳐 반복적으로 측정하되, 매번 상이한 대상을 측정한 데이터를 의미
합동 횡단면 데이터
- 지금까지는 동일한 실험 대상을 여러 시간대에 반복해서 관측한 데이터(ex. 레스토랑 할인이 판매에 미치는 효과)로 분석했다.
- 이러한 데이터는 단순화를 위해 횡단면 데이터로 취급함
8.1 패널 데이터
- 일반적으로 마케팅에서 누가 광고(T)를 보는지 통제할 수 없기에, 무작위 실험을 진행하는 것은 쉽지 않다.
- 새로운 사용자가 사이트를 방문했을 때, 마케팅 링크를 클릭해서 구입했다는 사실을 알아도, 만약 그 링크가 없었어도 사용자가 구매했을까?에 대한 답은 얻기 어렵다.
- 온라인보다도 오프라인에서의 인과효과 추정은 더 까다롭다.
- 이 질문에 답하기 위해 마케팅 업계에서는 일반적으로 지역 실험을 실행한다.
- 특정 지역에서 마케팅 캠페인을 집행하고, 이를 마케팅하지 않은 다른 지역과 비교

- date, city별로 정렬된 다운로드 수 데이터
- D는 처치 변수, t는 시간을 나타내는 데 사용
- T는 기간의 수를, Tpre는 개입 이전 기간을 나타냄
- 시간 벡터는 t = {1, 2, ... Tpre, Tpre+1, ...T}
- 개입 후 = 처치 후 기간 = Tpre + 1, ... T
- 더미변수 post (T) : t>Tpre일 때 1, 그렇지 않으면 0
- 마케팅 팀은 Di=1인 도시에서 오프라인 캠페인을 진행
- 처치 변수(D)와 개입 후(T)에 대한 조합은 W로 표기
- W = D * 1 (t > Tpre) 또는 W = D * Post
(mkt_data
.assign(w = lambda d: d["treated"]*d["post"]) # treated과 post의 곱으로 w라는 새로운 컬럼 생성
.groupby(["w"]) # 생성한 w 기준 그룹화
.agg({"date":[min, max]}))
- w = 0 (대조군, 개입 전) 기간은 21-05-01 부터 21-05-15까지이고,
- w = 1 (실험군, 개입 후) 기간은 21-05-15부터 21-06-01까지
처치 받은 도시들에서 오프라인 마케팅 캠페인 집행 후 미친 영향을 구해보자.

- 위의 ATT 수식은 캠페인 시작 후 (t > Tpre), 캠페인이 D = 1 도시들에 미친 영향만을 의미
- Yit(1) (↔실험군 캠페인 시작 후)은 관측 가능하므로, 누락된 잠재적 결과 E[Y(0)|D=1, Post=1] (↔실험군이 만약 캠페인을 진행안했을 때) 을 대체함으로써 ATT를 추정할 수 있음
패널데이터는 ① 대상 및 ② 시간에 걸친 상관관계를 활용하여 누락된 잠재적 결과를 추정할 수 있다.
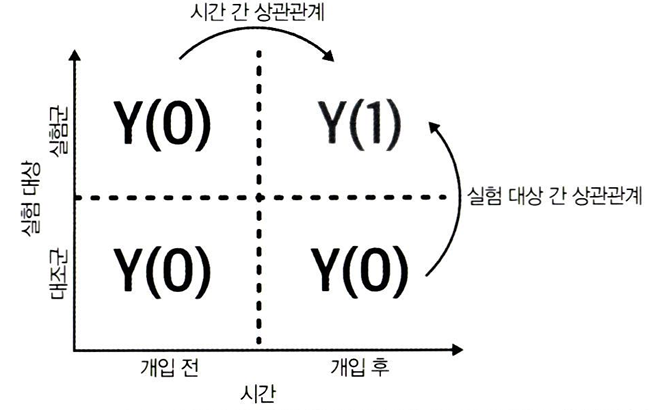
- 위의 행렬을 통해서 알 수 있듯이, 실험군에 대한 반사실 Y(0)을 추정하기가 훨씬 쉽기 때문에, ATT에 집중해야 한다.
- 반면 대조군에 대한 ATC를 구하기 위해 반사실 Y(1)을 추정하는 것은 어렵다. 해당 반사실을 관측할 수 있는 셀은 1개 뿐이기 때문
8.2 표준 이중차분법
이중차분법
: 기본 개념은 '관측된 실험군 기준값에 대조군 결과 추세를 보정하여, 누락된 잠재적 결과인 E[Y(0)|1, Post=1]을 추정하는 것이다. (↔ 만약 실험군이 처치 받지 않았으면 어떻게 됐을까?)

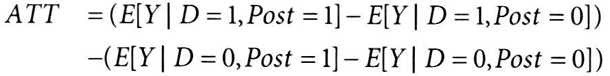
DID 추정 과정
- 데이터의 기간을 개입 전과 후로 나눈다.
- 실험 대상을 실험군과 대조군으로 나눈다.
- 마지막으로 4개의 셀 (개입 전 실험군과 대조군, 개입 후 실험군과 대조군) 모두의 평균을 계산한다.

did_data = (mkt_data
.groupby(["treated", "post"])
.agg({"downloads":"mean", "date": "min"}))
did_data
- 실험군의 기준 값 (개입 전) : E[Y|1, Post=0]에 대해 did_data.loc[1]을 사용하여 실험군을 찾은 다음, .loc[0]를 덧붙여 개입 전 기간으로 인덱싱
- 대조군의 추세 더하기 : E[Y|D=0, Post=1] - E[Y|D=0, Post=0]을 얻기위해, did_data.loc[0]을 사용해서 대조군을 찾아 diff()로 차이 계산, .loc[1]을 덧붙여 마지막행으로 인덱싱
y0_est = (did_data.loc[1].loc[0, "downloads"] # treated baseline
# 대조군 추세
+ did_data.loc[0].diff().loc[1, "downloads"])
att = did_data.loc[1].loc[1, "downloads"] - y0_est
att
> 0.6917359536407233
3. 기준값에서 1,2번으로 추정한 실험군의 잠재적 결과를 빼서 ATT 구하기
mkt_data.query("post==1").query("treated==1")["tau"].mean()
> 0.7660316402518457✅ 실제 사례: 최저임금과 고용
- 최저임금 인상(T)이 고용 감소(Y)로 이어진다는 전통적인 경제이론을 이중차분법을 사용해서 반론
- 뉴저지(T=1)와 펜실베니아(T=0)의 레스토랑에서, 뉴저지의 최저임금 인상 전후 데이터를 조사, 고용이 감소했다는 증거를 찾을수 없었고 경제 이론이 틀렸다는 사실이 확실히 입증됨
- 논문의 영향력과 이중차분법의 대중화에 기여한 공로로, 데이비드 카드는 21년에 노벨 경제학상을 받았다.
8.2.1 이중차분법과 결과 변화
이중차분법을 바라보는 첫 번째 관점
먼저 시간 차원에서 데이터를 구분하는 결과 변화 측면에서 접근해보자

pre = mkt_data.query("post==0").groupby("city")["downloads"].mean() # 개입 전 평균
post = mkt_data.query("post==1").groupby("city")["downloads"].mean() # 개입 후 평균
delta_y = ((post - pre)
.rename("delta_y")
.to_frame()
# 처치 더미변수 추가
.join(mkt_data.groupby("city")["treated"].max()))
delta_y.tail()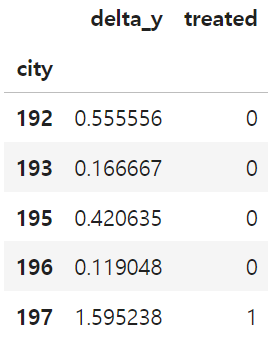
잠재적 결과 표기법을 사용하여 ATT를 △y에 대하여 정의하면,

△y0를 대조군 평균으로 대체하여 ATT를 식별하면,
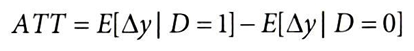
이 기댓값들을 표본 평균으로 대체하면, DID 추정량과 동일한 값을 얻을 수 있음
(delta_y.query("treated==1")["delta_y"].mean()
- delta_y.query("treated==0")["delta_y"].mean())
> 0.6917359536407155→ 위는 이중차분법의 가정인 E[△y0] = E[△y|D=0]을 잘 보여준다.

did_plt = did_data.reset_index()
plt.figure(figsize=(10,4))
# 대조군의 date별 downloads
sns.scatterplot(data=did_plt.query("treated==0"), x="date", y="downloads", s=100, color="C0", marker="s")
sns.lineplot(data=did_plt.query("treated==0"), x="date", y="downloads", label="Control", color="C0")
# 실험군의 date별 downloads
sns.scatterplot(data=did_plt.query("treated==1"), x="date", y="downloads", s=100, color="C1", marker="x")
sns.lineplot(data=did_plt.query("treated==1"), x="date", y="downloads", label="Treated", color="C1",)
# y축에 리스트 형태로 '대조군의 행사 후'와 '실험군의 반사실'을 입력하여 두 점을 잇는 점선을 그림
plt.plot(x=did_data.loc[1, "date"], y=[did_data.loc[1, "downloads"][0], y0_est], color="C2", linestyle="dashed", label="Y(0)|D=1")
plt.scatter(x=did_data.loc[1, "date"], y=[did_data.loc[1, "downloads"][0], y0_est], color="C2", s=50)
plt.xticks(rotation = 45);
plt.legend()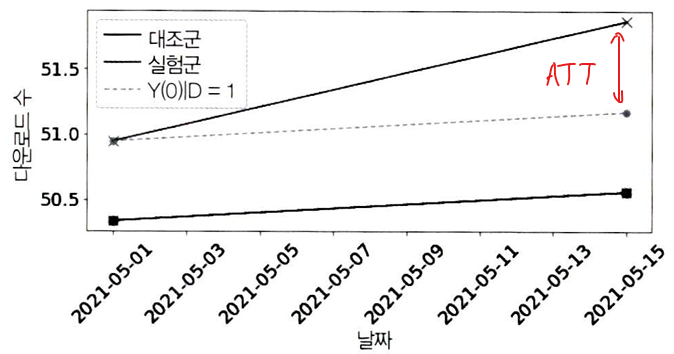
- E[Y(0)|D=1]의 DID 추정값(점선)은 대조군 추세를 실험군 기준값에 보정하여 얻은 결과
- 실험군의 행사 전(did_data.loc[1, "downloads"])[0] 값과 추정한 실험군의 반사실(행사 후 기간에 행사 미실행,y0_est) 값을 이은 점선이다.
- 추정된 ATT는 처치 후 기간에 추정된 반사실적 결과 Y(0)과 실제 실험군 결과 Y(1)의 차이이다.
8.2.2 이중차분법과 OLS
이중차분법을 바라보는 두 번째 관점
포화회귀모델(saturated regression model)을 사용하여 DID 추정량 얻기
- city와 post(개입)으로 그룹화하기
- city-post 조합의 일평균(mean) 다운로드 수 계산하기
- 기간의 시작 날짜(min)와 도시의 처치 여부(max) 확인하기
did_data = (mkt_data
.groupby(["city", "post"])
.agg({"downloads":"mean", "date": "min", "treated": "max"})
.reset_index())
did_data.head()
위의 데이터셋으로 다음 선형모델 추정

- 회귀계수 β^3은 DID 추정값
- β0 = 대조군 도시의 개입 전 (기준값)
- β0+β1 = 실험군 도시의 개입 전 (기준값)
- β1 = 실험군 도시와 대조군 도시 간의 기준값 차이
- β0+β2 = 대조군 도시의 개입 후
- 따라서 β2는 시간이 지남에 따라 발생하는 개입 전후의 변화량
- 따라서 개입 전후 실험군 도시의 downloads는 β0+β1+β2+β3으로 표현
- 여기서 β3는 실험군과 대조군 간의 차이와 + 시간 추세를 모두 고려한 DID 추정량, 즉 개입의 효과를 나타내는 증가분
import statsmodels.formula.api as smf
smf.ols(
'downloads ~ treated*post', data=did_data
).fit().params["treated:post"]
> 0.69173595364069048.2.3 이중차분법과 고정효과
이중차분법을 바라보는 세 번째 관점
이중차분법을 바라보는 세 번째 관점은 고정효과모델(unit-fixed effect model),즉 이원고정효과(TWFE)를 사용하는 것이다.

각 개체의 고유 특성과 시간의 고유 특성을 고정효과로 분리한 상태에서, 처치 효과(τ)가 어떻게 종속 변수 Yit에 영향을 미치는지에 대한 수식
- Yit = i번째 개체의 t 시간대 종속 변수 값
- τ = 처치효과
- Wit (=Di * Postt)= 처치 변수
- Di = 개체 i의 처치 여부
- Postt: t 시간대의 처치 전/후
- αi = 개별 대상i의 고정효과 (↔개체의 불변 특성)
- γt = 시간t의 고정효과 (↔시간의 불변 특성)
- eit = 오차 항, 설명되지 않은 변동성
위의 Yit 수식의 선형 회귀 모델에서 개체가 처치 후 기간에 처치를 받았는지 여부를 나타내는 이진 변수 생성

- Wit = 개체 i가 시간t에 처치를 받았는지 여부
- 실험군의 처치 후 기간에서 Di = 1, Postt = 1이면 Wit = 1이 되고, 나머지는 0이 된다.
위 모델을 추정하면 W와 관련된 매개변수 추정값이 DID 추정값과 일치하여 ATT를 구할 수 있다.
-
- 실험군 dummy와 처치 이후 dummy를 곱해서 W를 만든다.
m = smf.ols('downloads ~ treated:post + C(city) + C(post)', # Wi=Di*Posti->상호작용 항만 포함하기 위해 :연산자 사용
data=did_data).fit()
m.params["treated:post"]
> 0.69173595364070918.2.4 이중차분법과 블록 디자인
표준 이중차분법 설정에서는 개입 전/후 실험/대조군으로 나뉜 4개의 데이터 셀만 필요하다.
- 개입 전/후 기간을 하나의 블록으로 집계할 필요는 없다.
- 블록으로 집계되지 않은 경우, 블록 디자인을 활용할 수 있다.
블록 디자인(Block Design)
- 한 그룹은 처치 받지 않으며, 다른 그룹은 동일한 시간대에 처치 받는 대상들로 구성된다.
- 따라서 다른 시점에 실험 대상에 개입이 이뤄지는 일은 허용되지 않는다.
- 이 예제에서는 Di=1인 도시에서만 05-15~06-01까지 오프라인 캠페인을 진행했기에, 이러한 형식을 갖춤
이 블록 디자인을 시각화하여 시간에 따른 각 도시의 처치 배정을 확인하고, 이 방법을 통해 개입 후 실험군-대조군 차이가 변하는지 확인해보자.
import matplotlib.ticker as plticker
fig, (ax1, ax2) = plt.subplots(2,1, figsize=(9, 12), sharex=True)
# 도시별 처치여부(heatmap)
heat_plt = (mkt_data
.assign(treated=lambda d: d.groupby("city")["treated"].transform(max))
.astype({"date":"str"})
.assign(treated=mkt_data["treated"]*mkt_data["post"])
.pivot("city", "date", "treated")
.reset_index()
.sort_values(max(mkt_data["date"].astype(str)), ascending=False)
.reset_index()
.drop(columns=["city"])
.rename(columns={"index":"city"})
.set_index("city"))
sns.heatmap(heat_plt, cmap="gray", linewidths=0.01, linecolor="0.5", ax=ax1, cbar=False)
ax1.set_title("Treatment Assignment")
# 시간에 따른 다운로드 수(lineplot)
sns.lineplot(data=mkt_data.astype({"date":"str"}),
x="date", y="downloads", hue="treated", ax=ax2)
loc = plticker.MultipleLocator(base=2.0)
# ax2.xaxis.set_major_locator(loc)
ax2.vlines("2021-05-15", mkt_data["downloads"].min(), mkt_data["downloads"].max(), color="black", ls="dashed", label="Interv.")
ax2.set_title("Outcome Over Time")
plt.xticks(rotation = 50);
1. 히트맵

- 각 도시에 대한 특정 날짜의 처리 할당 상태를 나타냄
- 흰색 = 처치 O, 검정색 = 처치 X
- 처치가 특정 날짜 이후에 적용됨을 알 수 있음
2. 라인 플롯

- 시간에 따른 다운로드 수 변화와 처치 시점을 점선으로 표시
- 선 주위의 그림자는 신뢰구간을 나타냄 (데이터의 변동성 시각화)
- 실험군(T=1)은 개입 이후 다운로드 수가 약간 증가하는 경향을 보임
- 처치 시점 이후에 두 그룹의 다운로드 수 차이가 벌어지기 시작함을 시각적으로 확인할 수 있다.
실험군과 처치 후 기간에 대한 dummy와 상호작용 회귀하기
m = smf.ols('downloads ~ treated*post', data=mkt_data).fit()
m.params["treated:post"]
> 0.6917359536407226
또는 고정효과 모델 사용하기
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=mkt_data).fit()
m.params["treated:post"]
> 0.6917359536407017
이제 패널데이터의 신뢰구간에 대해 살펴보자.
8.2.5 추론
- 패널데이터에서의 추론은 굉장히 까다롭기 때문에 정확한 신뢰구간을 구하는 것이 어렵다.
- 그 이유는, N*T(ime)개의 데이터 포인트가 있어 동일한 실험 대상이 여러 번 나타나므로, 이들이 독립적이고 동일하게 분포되지 않았다는(iid, independent and identically distributed) 점이다.
- not independent: 같은 도시의 downloads 수는 월별로 연관되어있을 것
- not identically distributed: 각 도시는 고유의 특성을 갖고 있어 downloads 수 분포가 다를 것
- 패널 데이터에서 독립성인 건 전체 데이터 포인트 수(N*T)가 아닌, 독립적인 개체 수(N)이기에, iid 가정을 만족시키기 위해서는 N을 표본 크기로 봐야 한다.
- N이 아닌, 전체 데이터 N*T를 표본 크기로 사용하면, 데이터 포인트끼리 연관되어 있어 표준 오차(평균의 분포)가 실제보다 작게 계산되며, 결과적으로 과도하게 낙관적이게 된다.
- 그 이유는 회귀분석에서는 표준오차 계산 시 표본 크기(N)을 고려하기 때문에, 분모인 N이 실제보다 커지면 표준오차가 작아지기 때문
- 회귀분석에서 지나치게 낙관적인 표준오차를 보정하려면, 실험 대상별로 군집화하는 방법이 있다.
- 도시로 군집화하면, 군집 하나는 하나의 도시이기에 군집 내에서 관측값들이 iid가정을 만족한다.
- 그 이유는, N*T(ime)개의 데이터 포인트가 있어 동일한 실험 대상이 여러 번 나타나므로, 이들이 독립적이고 동일하게 분포되지 않았다는(iid, independent and identically distributed) 점이다.
군집 표준오차로 신뢰구간을 구해보자.
m = smf.ols(
'downloads ~ treated:post + C(city) + C(date)', data=mkt_data
).fit(cov_type='cluster', cov_kwds={'groups': mkt_data['city']}) # 군집 표준오차 사용
# 'city'를 군집 변수(cov_kwds)로 사용하여, 동일 도시 내 관측값들이 서로 독립적이지 않을 수 있음을 고려하여 표준 오차를 조정
print("ATT:", m.params["treated:post"])
m.conf_int().loc["treated:post"]ATT: 0.6917359536407017
0 0.296101
1 1.087370
Name: treated:post, dtype: float64신뢰구간은 (0.296~1.08) 이다.
기존 표준오차 신뢰구간과 비교해보자.
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=mkt_data).fit()
print("ATT:", m.params["treated:post"])
m.conf_int().loc["treated:post"]ATT: 0.6917359536407017
0 0.478014
1 0.905457
Name: treated:post, dtype: float64→ 군집표준오차 (0.296~1.08) 는 기존 오차 (0.478~0.905) 보다 신뢰구간이 더 넓다.
❗군집표준오차의 사용은 데이터의 군집 내 상관관계를 고려함으로써 신뢰구간을 넓힐 수 있다.
- 관측값들이 군집 내 서로 상관되어 있을 때 표준오차의 정확한 추정을 위해 필요
- 군집표준오차를 계산함으로써 군집 내의 변동성을 올바르게 반영하여 전체 표본의 변동성 추정값을 조정
- 이로 인해 군집 표준오차 계산 시 일반적으로 표준오차는 증가하고, 그 결과 신뢰구간이 넓어지는 경향이 있음
기존 데이터 mkt_data 대신 실험 대상과 처치 전후 기간별 집계한 데이터 did_data로 대체하고 신뢰구간을 확인해보자.


m = smf.ols(
'downloads ~ treated:post + C(city) + C(date)', data=did_data
).fit(cov_type='cluster', cov_kwds={'groups': did_data['city']})
print("ATT:", m.params["treated:post"])
m.conf_int().loc["treated:post"]ATT: 0.6917359536407091
0 0.138188
1 1.245284
Name: treated:post, dtype: float64신뢰구간이 (0.138~1.245)이다.
❗일자별 데이터(mkt_data)의 신뢰구간이 더 좁기에, 각 군집당 더 많은 시간대가 있으면 분산을 줄일 수 있음을 보여준다. (표본크기가 시간대가 아닌 실험 대상에 의해 결정되어야 한다는 점을 감안하더라도,)
✅ 블록 부트스트랩
: 표본의 종속성을 고려하여 샘플링하는 부트스트랩 방법
- 신뢰구간을 구하기 위해 전체 추정 과정을 부트스트랩하는 방법
- 반복되는 실험 대상이 있으므로, 동일 대상에 대한 모델의 오차는 상관될 수 있다. (동일 대상이더라도, 한 도시의 이번달 downloads가 다음달에 영향)
- 따라서 전체 실험 대상으로 복원 추출하여 동일 대상들의 관측값이 항상 함께 포함되도록 한다. (↔원래의 city값이 유지한 채로 샘플링됨)
- np.random.choice 함수로 실험 대상을 복원추출하는 함수를 만들고, Parallel과 delayed함수로 블록 부트스트랩 구현
먼저 실험 대상을 복원추출하는 함수 생성
- city의 고유한 값을 추출하여 블록 단위로 설정
- 고유한 블록 단위 중 복원 추출하여 표본을 만듦
- 데이터 프레임을 블록 단위로 인덱싱하고, 샘플링된 블록만을 선택
def block_sample(df, unit_col):
units = df[unit_col].unique()
sample = np.random.choice(units, size=len(units), replace=True)
return (df
.set_index(unit_col)
.loc[sample]
.reset_index(level=[unit_col]))
블록 부트스트랩 함수 생성
- 재현 가능한 결과를 위해 난수 생성기 초기화
- 병렬처리(Parallel)를 사용하여 부트스트랩 수행
- n_jobs=4 : 4개의 병렬 작업 사용
- 각 반복에서 block_sample 함수를 사용하여 샘플링된 데이터에 est_fn(선형회귀모델 fitting)함수 적용
- *delayed: 함수가 필요할 때 실행되도록 지연시키는 함수로, 함수 호출을 래핑(wrapping)하여, Parallel 객체가 이를 병렬로 실행할 수 있도록 한다.
from joblib import Parallel, delayed
def block_bootstrap(data, est_fn, unit_col,
rounds=200, seed=123, pcts=[2.5, 97.5]):
np.random.seed(seed)
stats = Parallel(n_jobs=4)(
delayed(est_fn)(block_sample(data, unit_col=unit_col))
for _ in range(rounds))
return np.percentile(stats, pcts)
블록 부트스트랩을 통해 신뢰구간을 계산해보자.
def est_fn(df):
m = smf.ols('downloads ~ treated:post + C(city) + C(date)',
data=df).fit()
return m.params["treated:post"]
block_bootstrap(mkt_data, est_fn, "city")array([0.23162214, 1.14002646])→ 군집 표준오차를 사용하여 얻은 구간 (0.296~1.08) 과 유사한 신뢰구간이 도출되었다. (↔블록 부트스트랩 함수가 잘 작동하고 있다는 좋은 지표)
→ 부트스트랩으로 신뢰구간을 구할 때, 실험군의 수가 적으면 표본에 실험군에 포함되지 않을 수 있다. 패널데이터를 이용한 추론이 아직 복잡한 주제이며, 명확한 해답이 없다.
8.3 식별 가정
이중차분법을 사용할 때 필요한 가정에 대해 알아보자.
8.3.1 평행 추세
- 앞장에서 횡단면 데이터를 다룰 때, 공변량X를 조건부르 둔 경우 T가 잠재적 결과와 독립이라는 식별 가정을 사용
- 이와 유사하지만, 더 약한 가정인 평행 추세(parallel trend)를 가정
평행추세가정
: 처치가 없으면 평균적으로 실험군과 대조군의 결과 추세가 동일할 것이라는 가정

위의 가정에서 E[Y(0)it = 1 | D = 1]은 관측할 수 없으므로, 위의 가정을 검증할 수 없다.

- 평행추세: 두 그룹이 평행한 트렌드를 보이는 경우
- 추정된 추세가 실제 Y(0)|D=1와 일치
- 평행 추세 가정을 만족하여 DID 추정량이 실제 ATT와 같아짐
- 수렴추세: 두 그룹이 서로 다른 트렌드를 보이는 경우
- 추정된 추세가 실제 Y(0)|D=1의 추세보다 가파름
- 로그 척도: 로그변환된 데이터의 비선형적 관계
- 평행 추세 가정이 척도에 따라 바뀔 수 있음을 보여준다.
- 평행 추세 가정을 만족하는 1번 그래프 데이터에 로그 변환을 적용했을 때,
- ex. 효과를 백분율 변화로 측정하고 싶은 경우, 결과를 백분율로 변환하면 추세가 엉망이 될 수 있으니 주의해야 한다.
✅ 평행 추세 가정과 독립성 가정의 연관성
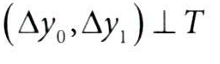
독립성 가정
: 실험군과 대조군에서 평균적으로 Y(0)의 수준이 동일하다고 가정하는 것
평행추세 가정
: 실험군과 대조군 간 Y(0)의 추세가 동일하다고 가정하는 것
- 패널데이터가 가지는 강력함은, 처치가 무작위로 배정되지 않더라도 실험군-대조군의 반사실 추세가 동일하다면, ATT를 식별할 수 있다는 점
- 조건부 독립성 가정처럼, 평행 추세 가정을 X에 따라라 조건부로 둘 수 있다.
8.3.2 비기대 가정과 SUTVA
패널데이터에서 이중차분법을 사용할 때 필요한 두 번째 가정은 비기대 가정으로, SUTVA와 연관되어있다.
SUTVA 위배 (Stable Unit Treatment Value Assumption)
: 실험군의 효과가 대조군으로 영향을 미칠 때 발생
- 이중차분법에서도 마찬가지이며, 실험 대상 뿐만 아니라, 시간 기간에 걸쳐서도 SUTVA가 위배될 수 있다.
- 즉, 개입이 아직 이뤄지지 않은 기간에, 파급 효과가 미리 나타나는 상황
- ex. 블랙 프라이데이 할인을 할 예정이라면, 그 이전에 이미 고객들이 제품을 찾는 시기가 되고, 처치 이전 기간에 Y 인 판매량이 급증하는 모습을 볼 수 있다.
- 패널 데이터에서 SUTVA를 만족시키는 것은 까다롭다. 특히 실험 대상이 지리적 영역일 때, 사람들이 끊임없이 지리적 경계를 넘나들며 이동하므로 대조군도 T의 영향을 받을 가능성이 높아 더더욱 어렵다.
공간적 파급효과
- 패널데이터 연구와 마찬가지로, 인과추론 학계에서 여전히 연구 중인 분야이다.
- 기본 개념은 대조군이 실험군에 충분히 가깝다고 간주되면, 값이 1인 더미변수 S를 사용하여, 이중차분법의 이원고정효과 공식을 확장하는 것
8.3.3 강외생성(strict exogeneity)


- 강외생성 가정은 고정효과모델에서의 '잔차'에 대한 가정이다.
- 강외생성 가정은 세 가지를 함축한다.
- 시간에 따라 변하는 교란요인 없음
- 피드백 없음
- 이월 효과 없음
위 세가지를 DAG를 통해 시각적으로 확인해보자.
8.3.4 시간에 따라 변하지 않는 교란요인
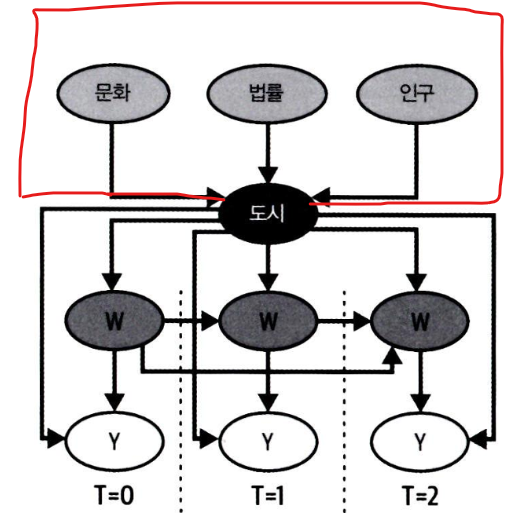
- 시간에 걸쳐 반복되는 관측값이 있으면, 관측되지 않는 교란요인이 존재하더라도 인과효과를 식별할 수 있다.
- 하지만 이 경우, 해당 교란요인이 시간에 따라 일정할 때 가능하다.
ex. 마케팅 예제에서, 특정 도시의 downloads(Y) 수가 시간에 따라 증가한다면, 적어도 단기적으로는 도시 문화의 변화 때문이 아닐 것이다. 그 이유는, 해당 교란 요인(도시 문화)이 시간에 따라 고정되어 있기 때문
- 여기서 시간 고정 교란 요인은 측정 불가능하므로, 통제할 수 없다.
- 하지만 실험 대상 자체를 통제함으로써 해당 시간 교란 요인을 통과하는 뒷문 경로를 차단할 수 있다.
데이터의 평균 제거 과정에서 시간 고정 공변량이 어떻게 사라지는지 확인해보자.
* 실험 대상 고정 효과를 추가하는 방법에는 ①더미 변수 추가 이외에 ②평균 제거 방법도 있었다.

- 평균을 제거하면, 관측되지 않은 Ui는 모두 사라진다.
- Ui는 시간에 걸쳐 일정하므로(일정하다고 가정) Ui = Ui바 가 되고,
- 따라서 모든 곳에서 Uit(..) = 0 이 된다. (← Uit(..) = Uit - Ui바)
- 요약하자면, 실험 대상 고정효과는 시간에 걸쳐 일정한 변수를 모두 없애버린다.
- 실험 대상 고정 효과 뿐만 아니라 시간에 따라 변하는 변수를 없애는 시간 고정효과에도 비슷한 논리를 적용할 수 있다.
- 이 마케팅 예제에서는, 시간 고정효과로 국가의 환율이나, 인플레이션 같은 요소가 예가 될 수 있다.
- 환율,인플레이션은 전국적인 변수이므로 모든 도시(실험 대상)에서 동일함
- 물론, 교란 요인이 시간에 따라 변한다면 앞서 배운 방법을 적용할 수 없다.
8.3.5 피드백 없음

- 피드백 없음 가정이란, 과거 결과인 Yit-1에서 현재 처치인 Wit로 향하는 화살표가 없다.
- 피드백이 없다는 것은, 처치가 결과 경로에 따라 결정될 수 없음을 나타낸다.
- 예를 들어 시간에 따라 인덱싱된 처치 벡터 W = (w0, w1, ... wT)를 가정했을 때, 이 시나리오에서는 전체 벡터가 한 번에 결정되어야 한다.
- 특정 시간대에 처치가 시작되어 무기한으로 계속되는 블록 디자인 안에서는 타당할 수 있다.
- 하지만 그럼에도 피드백없음 가정이 위반될 수 있다.
- ex. 마케팅 팀이 한 도시의 downloads 수가 1,000건에 도달할 때마다 오프라인 마케팅 캠페인 집행을 결정했다고 가정했을 때, 이는 피드백 없음 가정을 위배하는 것
순차적 무시 가능성
: 만약 과거 결과를 조건부로 두고자 한다면, 순차적 무시 가능성하에서의 방법을 살펴보아야 한다. 이를 통해서 과거 결과나 시간 고정 교란 요인 중 하나만 통제할 수 있다.
* Causal Inference with Time-Series Cross-Sectional Data: A Reflection 논문 참고
8.3.6 이월 효과와 시차종속변수 없음

a. 이월 효과 없음
- 이월 효과 없음이란, 과거 처치가 현재 결과에 영향을 주지 않는다는 가정이다.
- 다행히 이 가정은 만족하지 않는 경우에도, 모델 확장을 통해서 처치의 시차(lagged)버전을 포함시켜서 완화될 수 있다.
예를 들어 기간 t-1 의 처치가 기간 t의 결과에 영향을 준다면, 다음과 같이 모델을 구성할 수 있다.
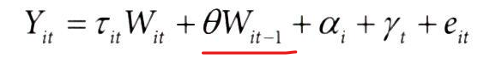
- 현재 처치의 영향 τWit : 현재 기간 t에서 처치 Wit가 종속 변수 Yit에 미치는 직접적인 영향
- 이전 처치의 영향 θWit-1 : 이전 기간 t-1에서 처치 Wit-1이 현재 기간 t의 결과 Yit에 미치는 영향을 추가로 반영. 이는 처치 효과가 즉시 나타나지 않고, 시간이 지나면서 영향을 미칠 수 있음을 나타낸다.
b. 시차종속변수(lagged dependent variable) 없음
- 과거 결과가 현재 결과의 직접적인 원인이 되지 않는다.
- 필수적인 가정은 아니다. 만족하지 않아도 식별에 큰 문제가 되지는 않음
'데이터 분석 > 인과추론' 카테고리의 다른 글
| [9-1] 실무로 통하는 인과추론 with 파이썬 - 9장. 통제집단합성법 (0) | 2024.06.23 |
|---|---|
| [8-2] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 (0) | 2024.06.16 |
| [7] 실무로 통하는 인과추론 with 파이썬 - 7장. 메타 러너 (0) | 2024.06.02 |
| [6] 실무로 통하는 인과추론 with 파이썬 - 6장. 이질적 처치효과 (0) | 2024.05.28 |
| [5-2] 실무로 통하는 인과추론 with 파이썬 - 5장. 성향점수 (0) | 2024.05.18 |




