| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 리프 중심 트리 분할
- 로그 변환
- 데이터 핸들링
- 3기가 마지막이라니..!
- 마케팅 보다는 취준 강연 같다(?)
- WITH CUBE
- XGBoost
- 캐글 산탄데르 고객 만족 예측
- 데이터 증식
- ImageDateGenerator
- 인프런
- 캐글 신용카드 사기 검출
- 그룹 연산
- pmdarima
- ARIMA
- Growth hacking
- 컨브넷
- WITH ROLLUP
- 그로스 마케팅
- 분석 패널
- splitlines
- 그로스 해킹
- 스태킹 앙상블
- DENSE_RANK()
- 데이터 정합성
- tableau
- sql
- 부트 스트래핑
- lightgbm
- python
- Today
- Total
LITTLE BY LITTLE
[9-1] 실무로 통하는 인과추론 with 파이썬 - 9장. 통제집단합성법 본문

목차
<9장. 통제집단합성법(Synthetic Control Method)>
9.1 온라인 마케팅 데이터셋
9.2 행렬 표현
9.3 통제집단합성법과 수평 회귀분석
9.4 표준 통제집단합성법
9.5 통제집단합성법과 공변량
9.6 통제집단합성법과 편향 제거
9.7 추론
9.8 합성 이중차분법
9.8.1 이중차분법 복습
9.8.2 통제집단합성법 복습
9.8.3 시간 가중치 추정하기
9.8.4 통제집단합성법과 이중차분법
9.9 요약
9장. 통제집단합성법

통제 집단합성법
: 대조군을 결합해서 처치가 없을 때의 실험군과 비슷한 가상의 대조군을 만드는 것
- 패널데이터는, 과거 자신과 비교할 수 있다는 점이 보다 타당한 가정 하에서 반사실의 추정을 가능하게 했다.
- 그리고 패널데이터셋에 널리 사용되는 이중차분법은, 실험군과 대조군의 평행 추세를 가정함으로써 처치효과를 식별할 수 있었다.
- 그러나, 이중차분법은 기간 T보다 많은 실험 대상 N이 있는 경우에 잘 작동하고, 반대의 경우 그렇지 못하다.
- 통제집단합성법은 아주 적은 수의 실험 대상, 심지어 실험군이 하나일 때에도 잘 작동하도록 설계되었다.
- 가상의 대조군이 잘 구성되기만 하면, 평행 추세 가정이 필요 없어진다.
9.1 온라인 마케팅 데이터셋
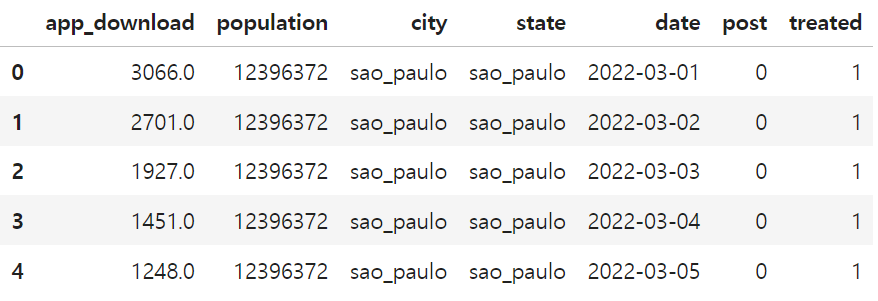
- city를 실험대상으로 하고, date를 시간 차원으로 하며 city에 대한 처치 여부를 표시하는 열 treated과 개입 전후 기간을 표시하는 열 post가 있다.
- 마케팅 캠페인은 실험군에 해당하는 city에 동시에 진행되므로, 단순한 블록 디자인을 가짐
- 실험군에 속하는 cty는 3개로 적은 편
- 결과변수는 app_download(일별 앱 다운로드 수)
- population, state와 같은 보조 정보
treated = list(df.query("treated==1")["city"].unique())
treated
> ['sao_paulo', 'porto_alegre', 'joao_pessoa']→ 처치 대상 도시는 총 3개
population 컬럼을 보면, 도시마다 인구 수가 달라 결과 변수에 영향을 미치므로, 시장 규모에 따라 결과 정규화하기
: app_download / population
df_norm = df.assign(
app_download_pct = 100*df["app_download"]/df["population"]
)
df_norm.head()
처치가 시작된 기간 확인
tr_period = df_norm.query("post==1")["date"].min()
tr_period
> Timestamp('2022-05-01 00:00:00')
시각화
np.random.seed(123)
df_sc = df_norm.pivot("date", "city", "app_download_pct")
ax = df_sc[treated].mean(axis=1).plot(figsize=(15,6), label="$E[Y|D=1]$")
# vlines로 처치 시작 시점 표시
ax.vlines(tr_period, 0, 0.07, ls="dashed", label="$t=T_{pre}+1$")
ax.legend()
# 대조군만 선택한 후, 20%만 plotting
df_sc.drop(columns=treated).sample(frac=0.2, axis=1).plot(color="0.5", alpha=0.2, legend=False, ax=ax)
plt.ylabel("app_download_pct")
- 실험군에 속한 세 도시의 평균 결과
- 대조군 도시의 표본 (연한 회색)
- 처치 후 기간 시작 선 (세로 점선)
→ 개입 후 실험군의 결과가 증가한듯하나, 마케팅 효과인지 확실치 않음
→ 조건부가 아닌 과거 결과를 사용하여 반사실 E[Y0|D=1, POST=1]을 추정해야 한다.
9.2 행렬 표현
- 패널 데이터를 행렬로 나타내면 한 차원은 기간, 다른 차원은 실험 대상이 된다.
- 행은 기간, 열은 도시(실험 대상)라고 가정해보자.

- (왼쪽 위) 처치 전-대조군, (오른쪽 위) 처치 전-실험군, (왼쪽 아래) 처치 후-대조군, (오른쪽 아래) 처치 후-실험군에 해당
- 처치 지표 wti는 처치 이후 기간의 실험군인 오른쪽 아래를 제외한 모든 곳에서 0이다.
잠재적 결과 행렬을 만들어보면,

ATT = Y(1)post, tr - Y(0)post, tr를 추정하기 위해서, Y(0)post,tr을 구하기 위해 나머지 세 블록 Y(0)pre,co, Y(0)pre,tr, Y(0)post,co를 모두 활용할 수 있다.
코드로 데이터를 행렬 형태로 구현해보자
1. date와 city별 결과를 보기 위해서 pivot() 메소드로 데이터프레임을 재구성한다.

df_pivot = df.pivot(index=time_col, columns=geo_col, values=y_col)
2. 결과 행렬에 대한 값을 실험군-대조군으로 나누고, 다시 개입 전-후 기간으로 나눈다.




def reshape_sc_data(df: pd.DataFrame,
geo_col: str,
time_col: str,
y_col: str,
tr_geos: str,
tr_start: str):
df_pivot = df.pivot(time_col, geo_col, y_col)
y_co = df_pivot.drop(columns=tr_geos)
y_tr = df_pivot[tr_geos]
y_pre_co = y_co[df_pivot.index < tr_start]
y_pre_tr = y_tr[df_pivot.index < tr_start]
y_post_co = y_co[df_pivot.index >= tr_start]
y_post_tr = y_tr[df_pivot.index >= tr_start]
return y_pre_co, y_pre_tr, y_post_co, y_post_tr
9.3 통제집단합성법과 수평 회귀분석
- 통제집단합성법의 핵심 개념은, 처치 이전 기간을 사용하여 대조군을 결합하는 것
- 수학적으로 이 개념을 최적화 문제로 접근했을 때, 실험 대상마다 부여되는 가중치 wi를 찾게 된다. (wit=Postt*Di와 다른 개념)
- 이 가중치 wi를 실험 대상별로 곱했을 때 (= wiyi) 실험군의 결과와 비슷한 값을 얻도록 하는 것이 최적화 목표

선형회귀분석에서 회귀분석을 결과와 공변량 X의 선형 조합 간의 (제곱) 차이를 최소화하는 것을 목표로 하는 최적화 문제로 표현할 수 있는 것과 유사하다.
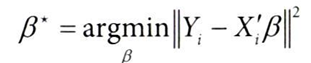
✅결과 모델링
6장. 성향점수의 이중강건추정량
m0 = LinearRegression().fit(X[df[T]==0, :], df.query(f"{T}==0")[Y])
m1 = LinearRegression().fit(X[df[T]==1, :], df.query(f"{T}==1")[Y])
m0_hat = m0.predict(X)
m1_hat = m1.predict(X)
- 통제집단합성법은 5장 성향점수에서 이중 강건 추정을 다룰 때 보았던 잠재적 결과 모델링과 유사하다.
- 잠재적 결과 모델링 시 대조군에서 추정된 회귀 모델(m0)으로 실험군의 잠재적 결과 Y0를 추정하고(↔ m1_hat), 실험군에서 추정된 회귀 모델(m1)으로 대조군의 잠재적 결과 Y1을 추정 (↔ m0_hat) 했다.
통제집단합성법에서의 목표도 동일하다.
- 대조군의 결과를 특성으로 사용해서, 실험군의 평균 결과를 예측하는 회귀라고 볼 수 있다.
- 개입 이전의 기간만 사용하여, 회귀분석을 통해 E[Y0|D=1]를 추정하는 것
앞서 만든 공변량 행렬로 OLS를 사용하여 가상의 대조군을 만들어보자.
X: 개입 이전-대조군 (↔y_pre_co)

결과 Y: 개입 이전-실험군(↔y_pre_trt)

from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=False)
model.fit(y_pre_co, y_pre_tr.mean(axis=1))
# 가중치 추출
weights_lr = model.coef_
weights_lr.round(3)array([-0.65 , -0.058, -0.239, 0.971, 0.03 , -0.204, 0.007, 0.095,
0.102, 0.106, 0.074, 0.079, 0.032, -0.5 , -0.041, -0.154,
-0.014, 0.132, 0.115, 0.094, 0.151, -0.058, -0.353, 0.049,
-0.476, -0.11 , 0.158, -0.002, 0.036, -0.129, -0.066, 0.024,
-0.047, 0.089, -0.057, 0.429, 0.23 , -0.086, 0.098, 0.351,
-0.128, 0.128, -0.205, 0.088, 0.147, 0.555, 0.229])
→ 각 대조군에 해당하는 도시마다 하나의 가중치가 있다.
✅수평 회귀분석

- 기존 회귀분석에서는 행은 실험대상, 열이 공변량이었다면, 수평 회귀분석에서는 행이 기간, 열이 실험대상으로, 데이터를 뒤집어서 실험 대상을 마치 공변량처럼 사용한다.
- 일반적으로 회귀분석은 실험 대상이 많을 때, 즉 N이 클 때 사용된다.
- 따라서 실험 대상이 적지만, 시간 범위가 더 길 때, 수평 회귀분석에서는 기간이 행에 오기 때문에, 통제집단합성법이 잘 작동한다.
OLS(y_pre_tr~y_pre_co)로 회귀계수(↔가중치)를 추정하고 나면, 이를 사용하여 개입 전 기간뿐만 아니라 전체 기간의 E[Y0|D=1]를 예측할 수 있다.
가중치 wi를 실험 대상별로 곱해서(= wiyi) 가상의 대조군 y0_tr_hat 만들기
# wi * yi (내적) 구하기
y0_tr_hat = y_post_co.dot(weights_lr) # y0_tr_hat = model.predict(y_post_co)과 동일한 결과 출력
y0_tr_hat
❗ 실험군 평균 결과를 재현하는 하나의 가상의 대조군 대신, 실험군 대상별로 각각의 가상의 대조군을 적합시킨 후에 평균을 구할 수도 있다.
model = LinearRegression(fit_intercept=False)
model.fit(y_pre_co, y_pre_tr)
y0_tr_hat = model.predict(y_co).mean(axis=1)
가상의 대조군 결과를 시각화해보면 다음과 같다.
plt.figure(figsize=(10,4))
y_co = pd.concat([y_pre_co, y_post_co])
y_tr = pd.concat([y_pre_tr, y_post_tr])
# x = date, y = synthetic control
plt.plot(y_co.index, model.predict(y_co), label="가상의 대조군 평균 결과", ls="-.")
plt.plot(y_tr.mean(axis=1), label="실험군 평균 결과")
plt.vlines(pd.to_datetime("2022-05-01"), 0, 0.04, ls="dashed", label="$t=T_{pre}+1$")
plt.xticks(rotation=45)
plt.ylabel("일별 앱 다운로드 수(app_download_pct)")
plt.legend(fontsize=14)
- 개입 시점 이후에, 예측된 값(가상의 대조군)이 실험군의 실제 결과보다 낮다. 즉 효과가 있다.
ATT를 추정하고 시각화해보면,
att = y_post_tr.mean(axis=1) - y0_tr_hatplt.figure(figsize=(10,4))
plt.plot(y_tr.mean(axis=1) - model.predict(y_co), label="ATT", ls="-.")
plt.vlines(pd.to_datetime("2022-05-01"), att.min(), att.max(), ls="dashed", label="$t=T_{pre}+1$")
plt.hlines(0, y_tr.index.min(), y_tr.index.max())
plt.ylabel("ATT")
plt.xticks(rotation=45)
plt.legend()
- 효과가 정점에 이르기까지 일정 시간이 걸리며, 정점에 이른 이후 점차 줄어든다.
- 마케팅에서는 광고를 본 후 사람들이 행동을 취하는 데까지 시간이 걸리므로 점진적 증가가 자주 관찰됨
- 그리고 효과가 사라지는 현상은 보통 시간이 지나며 서서히 사라지는 '신기 효과(novelty effect)'때문
- 개입 이전의 ATT 크기는 0에 가까울 수록 좋다.
- 개입 이전의 ATT는 단순히 OLS 모델의 잔차(표본오차)이므로, 오차가 낮을 수록 좋은 것(↔ 가상의 대조군이 잘 생성된 것)
- 하지만, 너무 낮으면 OLS 모델이 과적합되었을 수 있다.
❗ 일반적으로 가상의 대조군을 구성할 때 단순회귀를 사용하지는 않는다.
- 상대적으로 많은 열(대조군의 도시들) 때문에 개입 후 기간에 일반화되지 않고 과적합되는 경향이 존재하기 때문
- 따라서 통제집단합성법은 단순회귀분석이 아닌, 합리적이고 직관적인 제약조건을 부여하는 방법이다.
통제집단합성법이 어떤 제약조건을 설정하는지 살펴보자.
9.4 표준(canonical) 통제집단합성법
가중치를 조정하여 실험군의 처치 전 데이터를 잘 설명하는 가상의 대조군을 만드는 방법
표준 통제집단합성법 공식은 회귀 모델에 2가지 제약조건을 부여한다.
- 가중치는 모두 양수 ( ω ≥ 0 & 1-ω≥ 0 )
- 가중치의 합은 1 (ω + (1-ω) = 1 )
→ 제약조건의 목적: 가상의 대조군이 실 험군에 대한 볼록 조합이 되도록하여, 외삽을 피하기 위함
✅ 블록조합
- 볼록 조합은 볼록 집합의 정의와 속성을 반영하여 명명됨
- 볼록 집합은 집합 S의 임의의 두 점 a와 b를 잇는 선분 ωa+(1− ω)b 이 항상 집합 S안에 존재하는 것
- 여러 벡터의 가중평균으로, 각 가중치는 0 이상이고, 합은 1이 되어야 하는 조합
- ex. 벡터 a와 b의 볼록 조합은 ωa+(1− ω)b (0<ω<1)
- 외삽을 피함으로써, 가능한 가중치의 범위를 제한하고, 주어진 조건에서만 만족하는 특정 값을 찾을 수 있음
- 위 예시에서 가중치 ω가 1보다 크거나, 0보다 작으면, 벡터 a와 b의 범위를 벗어난 값을 생성함
- 이는 모델의 일반화 능력을 향상시키고, 더 신뢰할 수 있는 추정값을 제공함

* ∥a−b∥^2=(a1−b1)^2+(a2−b2)^2+(a3−b3)^2
위 두가지 제약조건이 고려된 최적화 함수이다.
- 대조군(Ypre,co)의 가중치(Wco) 조합(=Ypre,co*Wco)으로 실험군의 처치 전 관측값(Ypre,tr)을 얼마나 잘 설명할 수 있는지를 나타낸다.
- 목표는 이 실험군의 처치 전 관측 값과 대조군의 가중치 조합의 차이를 최소화하는 것
- 제약 조건(subject to..)
- ∑iωi=1: 가중치의 합이 1이 되어야 한다 → 가중치가 확률로 해석될 수 있도록
- : 모든 가중치는 0보다 커야 한다. → 각 대조군 단위가 가중치에 기여할 수 있도록
표준 통제집단합성법을 코드로 구현해보자.
- 볼록 최적화 라이브러리(cvxpy.cvxpy)를 사용하여 cp.Minimize로 최적화 목표 정의
- 통제집단 합성법의 최적화 함수 입력
- 최적화 제약조건 설정
from sklearn.base import BaseEstimator, RegressorMixin
from sklearn.utils.validation import (check_X_y, check_array,
check_is_fitted)
import cvxpy as cp
class SyntheticControl(BaseEstimator, RegressorMixin):
def __init__(self,):
pass
def fit(self, y_pre_co, y_pre_tr):
y_pre_co, y_pre_tr = check_X_y(y_pre_co, y_pre_tr)
w = cp.Variable(y_pre_co.shape[1]) # 가중치 변수 정의
objective = cp.Minimize(cp.sum_squares(y_pre_co@w - y_pre_tr)) # 목적 함수 정의
constraints = [cp.sum(w) == 1, w >= 0] # 제약 조건 정의
problem = cp.Problem(objective, constraints) # 최적화 문제 설정
self.loss_ = problem.solve(verbose=False) # 최적화 문제 해결
self.w_ = w.value # 추정된 모델의 최종 손실을 저장하여 모델에 공변량을 추가할 때 활용 가능
self.is_fitted_ = True
return self
def predict(self, y_co):
check_is_fitted(self)
y_co = check_array(y_co) # 입력된 대조군 데이터 y_co에 대해
return y_co @ self.w_ # 최적화된 가중치 self.w를 적용하여 예측 값 계산model = SyntheticControl()
model.fit(y_pre_co, y_pre_tr.mean(axis=1))
# 가중치 구하기
model.w_.round(3)[Out]
array([-0. , -0. , -0. , -0. , -0. , -0. , 0.076, 0.037,
0.083, 0.01 , -0. , -0. , -0. , -0. , -0. , -0. ,
0.061, 0.123, 0.008, 0.074, -0. , 0. , -0. , -0. ,
-0. , -0. , -0. , -0. , -0. , 0. , -0. , 0.092,
-0. , -0. , 0. , 0.046, 0.089, 0. , 0.067, 0.061,
0. , -0. , -0. , 0.088, 0. , 0.086, -0. ])- 볼록성 제약조건은 최적화 문제에 대한 희소해결책(↔가중치가 0인 부분이 많음)을 준다.
- 최종 가상의 대조군을 만드는 데에는 소수의 도시만 사용된다는 의미
통제집단합성법으로 가상의 대조군의 추정값을 얻은 뒤, ATT 추정값 계산
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(15,8), sharex=True)
# 제약 조건이 없는 회귀분석 결과도 시각화하여 비교
ax1.plot(y_co.index, model.predict(y_co), label="Synthetic Control")
ax1.plot(y_tr.mean(axis=1), label="실험군", ls="-.")
ax1.vlines(pd.to_datetime("2022-05-01"), 0, 0.04, ls="dashed", label="$T_0$")
ax1.legend()
ax1.set_ylabel("ATT")
# 통제집단합성법 결과 시각화
ax2.plot(y_co.index, y_tr.mean(axis=1) - model.predict(y_co), label="효과", ls="-.")
ax2.hlines(0, y_co.index.min(), y_co.index.max())
ax2.vlines(pd.to_datetime("2022-05-01"), -0.01, 0.015, label="$T_0$")
ax2.legend()
ax2.set_ylabel("앱 다운로드 수(app_download_pct)")
plt.xticks(rotation=45);
- 제약조건이 없는 회귀분석 결과(상단)와 비교했을 때, 정규화로 인해 처치 전 오차는 커졌지만, 처치 후 ATT는 잡음이 줄어들었다.
❗통제집단합성법은 수평 회귀분석에 불과하기에, 라쏘나 릿지와 같은 다른 정규화하는 방법을 고려할 수 있다.
*단, 실험 대상이 지역인 경우 지역 간 결과가 양의 상관관계인 경향이 있으므로, 음의 가중치는 허용하지 않는 것이 좋다.
✅ 통제집단합성법에 대한 가정
- 이중차분법과 마찬가지로, ① 처치에 대한 비기대 가정과 ② 파급 효과없음 가정을 만족해야 한한다.
- 가정에 있어서 이중차분법과의 차이점은, 잠재적 결과 모델에 대한 매개변수 가정이다.
잠재적 결과에 대한 매개변수 가정
- 이중차분법에서는 실험군의 Y0추세가 대조군의 Y0추세와 평행하다고 가정
- 통제집단합성법에서는 벡터자기회귀모델(VAR, Vector Autoregressive) 이나 선형인자모델(linear factor model)과 같이 잠재적 결과에 대해 더 유연한 모델을 허용함

- 위 식에서 λ1=1, f1=βt, λ1=αi, f1=1이면, 이원고정효과모델(Y0it = αi + βt + eit) 의 일반화 버전임을 알 수 있다.
- 잠재적 결과가 벡터자기회귀모델이나 선형인자모델을 따르고, 가상의 대조군이 실험군과 비슷하다면, 통제집단합성법이 ATT에 대해 편향되지 않은 추정값을 생성한다고 주장됨
'데이터 분석 > 인과추론' 카테고리의 다른 글
| [10] 실무로 통하는 인과추론 with 파이썬 - 10장. 지역 실험과 스위치백 실험 (0) | 2024.07.16 |
|---|---|
| [9-2] 실무로 통하는 인과추론 with 파이썬 - 9장. 통제집단합성법 (0) | 2024.06.29 |
| [8-2] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 (0) | 2024.06.16 |
| [8-1] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 (0) | 2024.06.11 |
| [7] 실무로 통하는 인과추론 with 파이썬 - 7장. 메타 러너 (1) | 2024.06.02 |




