[6] 실무로 통하는 인과추론 with 파이썬

Notice

Recent Posts

Recent Comments

Link

« 2024/07 »
일	월	화	수	목	금	토
	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28	29	30	31

Tags more

Archives

Today

Total

관리 메뉴

LITTLE BY LITTLE

[6] 실무로 통하는 인과추론 with 파이썬 - 6장. 이질적 처치효과 본문

데이터 분석/인과추론

[6] 실무로 통하는 인과추론 with 파이썬 - 6장. 이질적 처치효과

위나 2024. 5. 28. 00:25

<6장 이질적 처치효과>

6.1 ATE에서 CATE로
6.2 예측이 답이 아닌 이유
6.3 회귀분석으로 CATE 구하기
6.4 CATE 예측 평가하기
6.5 모델 분위수에 따른 효과
6.6 누적 효과 곡선
6.7 누적 이득 곡선
6.8 목표 변환
6.9 예측 모델이 효과 정렬에 좋을 때

6.9.1 한계 수확 체감
6.9.2 이진 결과

6.10 의사결정을 위한 CATE
6.11 요약

6장. 이질척 처치효과

이전까지는 처치의 평균적인 영향을 살펴보았다면, 이번 장에서는 처치가 사람마다 어떻게 다른 영향을 미치는지에 초점을 맞출 것
처치 효과는 일정하지 않기에, 어떤 대상이 처치에 더 잘 반응하는지 아는 것은 처치 대상을 결정하는 데 중요한 역할을 한다.
즉, 이질적 효과는 "개인화"라는 개념에 대해 인과추론으로 접근할 수 있는 길을 열어준다.
또한, 예측 문제에서 교차 검증과 모델 선택의 아이디어가 이질적 처치 문제에도 적용됨을 확인
이질적 효과 추정을 검증하는 일은 단순 예측 모델 평가보다 훨씬 복잡하기에, 새로운 방법을 살펴봄

6.1 ATE에서 CATE로

: 이진 처치의 경우 알맞은 실험 대상에만 처치하고,
연속형 처치의 경우 각 대상에 맞는 최적의 처치 수준을 파악하는 것이 목표

"누구"에게 처치해야 하는지에 관한 다른 유형의 결정을 내리는 방법을 배워보자.
개인화를 위한 한 가지 방법은, 이질적 효과를 고려해서 조건부 평균 처치효과(CATE)를 추정하는 것
모든 대상이 처치에 동일하게 반응하지 않는다고 가정하고, 이러한 이질적 효과를 활용하고자 함

개인화 적용 사례

일 년 중 어떤 날에 판매해야 효과적일까?
제품 가격을 얼마로 책정해야 할까?
개인별로 어느 정도의 운동이 과한 운동일까?

6.2 예측이 답이 아닌 이유

Y대신 그룹별 기울기(β1) 구하기

✅EX. 가격,할인,금리 등 고객 특성(X)에 따라 다른 할인(T)을 제공하고자 함

이 개인화 부분은 '고객 세분화' 문제로 생각할 수 있다.

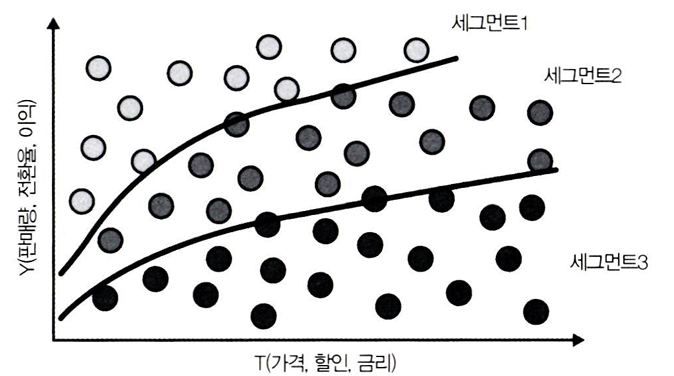
각 고객에 대한 조건부 처치효과인 기울기 δY/δT 를 구할 수 있다면,
처치에 잘 반응하는 고객과 그렇지 않은 고객을 그룹으로 나눌 수 있을 것이다.
이를 기존 머신러닝 접근법과 비교해보자.
→ 머신러닝은 각 실험 대상의 도함수 δY/δT 가 아닌, Y를 예측하려고 할 것이다.

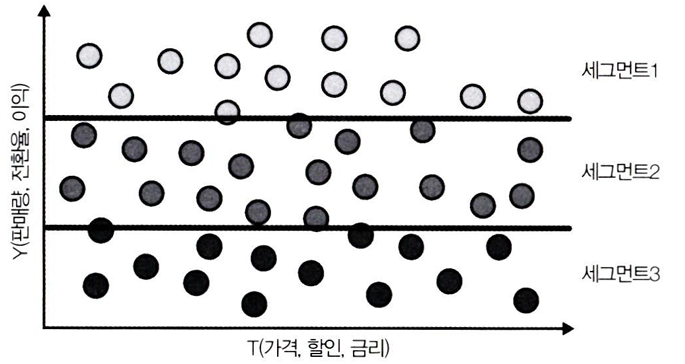
이렇게 하면 기본적으로 y축에 따라 공간을 분할하게 되며, 예측 모델이 목표에 잘 근사할 것이라 가정한다.
이 방법으로는 처치효과가 다른 그룹들을 찾을 수 없다.
단순 결과 예측이 항상 의사결정에 도움 되는 것은 아님

각 실험 대상의 도함수 δY/δT ( δ Sales / δ Discount )를 관측할 수 없다면, 기울기를 어떻게 예측할 수 있을까?
결과 Y와 다르게, 기울기는 기본적으로 개별 대상 수준에서 관측할 수 없다.
→ 처치가 T에서 T+ϵ 로 변할 때 Y의 변화율 예측하기

실험 대상의 개별 기울기를 확인하려면, 다양한 처치 조건에서 각각의 실험 대상을 관측하고, 각 처치에 따른 결과Y의 변화를 계산해야 한다.

✅CATE와 ITE

특정 조건 하에서 평균 처치효과와 개별 실험 대상에 대한 처치효과

일반적으로 치사율이 50%인 질병에 걸린 환자에게 신약이 미치는 효과를 알고자 함

그룹1의 경우, 모두 사망했기 때문에, 개별 처치효과 ITE는 실제로 더 나쁜 결과
그룹2의 경우, 1명만 사망했기에 실제효과는 기대치와 일치
→ 그 어떤 실험 대상의 ITE도 0.5가 아니다.

6.3 회귀분석으로 CATE 구하기

: T와 X간의 상호작용 항을 모델에 포함시켜 CATE 추정하기

대부분의 응용 인과추론과 마찬가지로 답은 선형회귀에서 시작된다.

✅ 레스토랑에서 고객에게 할인을 제공해야 하는 적절한 시기를 파악하고자 하는 상황을 가정해보자.

여기에서는 분석 단위가 '고객'이 아닌, '요일-레스토랑' 조합이다.
이전과 같은 추론 방법을 적용하되, 고객 대신 요일에 '처치'(할인 제공)를 하게 된다.
이를 CATE 추정 문제로 생각해보자.

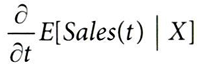
1-1. 일반적인 선형모델

1-2. 일반적인 선형모델을 처치(T)에 대해 미분해서 얻을 수 있는 결과

→ 모든 대상에 대해 상수인 β1 추정량을 구할 수 있다.
→ 하지만 모든 실험 대상(일자-레스토랑 조합)의 기울기 예측값이 동일하므로,
언제 할인을 해야 하는지 파악하는 데 도움이 되지 않음

2-1. 변화를 준 선형모델

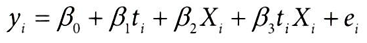
2-2. 변형된 선형모델을 처치(T)에 대해 미분해서 얻을 수 있는 결과

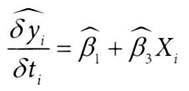
→ 각기 다른 Xi로 정의된 개별 대상마다 기울기 예측값이 다르게 나올 것
→ 직관적으로, 처치 T와 공변량 X간의 상호작용을 모델에 포함함으로써, 해당 공변량(Xi)에 따라 효과가 어떻게 변하는지 모델이 학습할 수 있다.

✅ 실제 사례: 가격 차별(price diescrimination)
: 이 장에서 다룬 내용을 미시경제학에서는 '가격 차별'이라 한다.
가격 차별이란, 기업이 더 큰 비용을 지불할 의사가 있는 소비자와 그렇지 않은 소비자를 구별해 더 큰 비용을 청구하는 것을 말함
ex. 시점간(intertemporal) 가격 차별
: 항공사에서 항공권을 언제 구입하는지에 따라 항공료를 다르게 책정하는 경우
→ 다음주 항공편을 예약해야 하는 고객은 내년 항공편을 예약하는 고객보다 훨씬 더 큰 비용을 지불
→ 시점에 따른 고객의 가격 민감도 구별

레스토랑에서 고객에게 할인을 제공해야 하는 적절한 시기를 파악하기 위한 과정을 코드로 구현해보자

6.3.1 공변량(Xi) 정의 & 공변량(X)과 처치(T)의 상호작용 항 포함시키기

날짜별 특성
1. month
2. weekday
3. is_holiday
4. 경쟁업체의 평균 가격 (각 레스토랑에서의 할인에 대한 고객 반응에 영향을 미칠 수 있음)

import statsmodels.formula.api as smf

X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"] # 공변량 정의
regr_cate = smf.ols(f"sales ~ discounts*({'+'.join(X)})", 
# '*'연산자는 상호작용 항을 포함하는 것을 의미
# '+'.join(X)는 X리스트를 +로 연결해서 문자열로 만드는 것
# 즉, discounts*({'+'.join(X)}) = discounts*(C(month) + C(weekday) + is_holiday + competitors_price)
# 곱셈(상호작용) 항만 원할 때는 ':' 연산자 사용
                    data=data).fit()

6.3.2 기울기 구하기

β^1 : 할인에 대한 계수
β^3 : 상호작용 항에 대한 계수

두 가지 기울기를 구하는 방식

적합된 모델에서 해당 매개변수를 추출하기
도함수 정의 사용하기

: β^1, β^3 각각을 구하는 대신에 도함수 δY/δT 구하기

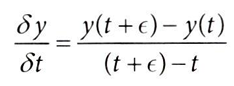
ε →0으로 갈 때, ε 를 1로 대체하면, 다음과 같이 근사할 수 있다.

(여기서 y^은 모델의 예측값을 의미하고, 선형 모델이기에 해당 근사치는 정확하다고 볼 수 있다.)

즉, 모델을 활용해 다음의 두 가지를 예측한 후, 차이(② - ①)를 CATE 예측값으로 구한다.
① 원본 데이터를 그대로 사용한 예측
② 원본 데이터를 사용하지만, 처치를 한 단위씩 증가시킨 예측

ols_cate_pred = (
    regr_cate.predict(data.assign(discounts=data["discounts"]+1)) #처치를 1 증가시킨 예측값
    -regr_cate.predict(data)
)

6.3.3 모델 평가하기

실제 처치 효과가 개별 수준에서 관측되지 않기에, 실젯값과 예측값을 비교하는 것은 불가능하다.
인과 추론 모델을 적용하는 데 있어서 경영진이 모델을 신뢰하도록 설득하는 건 매우 어려움
- ml이 큰 성공을 거두기 시작한 건 예측 모델 검증이 매우 간단했기 때문이라고 함
- 인과추론의 경우 hold-out 패러다임(trian,test set으로 분할하는 기법)과 같은 검증 방법은 명확하지 않음
- 그 이유는, "관측할 수 없는 양(δY/δT)"을 추정하는 데 관심이 있기 때문

t와 y사이 선의 기울기로 표현되는 모든 개체에는 내제된 반응이 있는 것처럼 보이나, 측정 불가능함

→ 개별적인 민감도 추정은 불가능하지만, 민감성을 "집계"함으로써, 민감도를 추정하는 방법을 소개한다.

6.4 CATE 예측 평가하기

: CATE 예측은 일반 머신러닝 예측과 유사한 방법론을 사용하나, 처치효과의 개인별 차이를 추정하는 것이 목표

6.4.1. 데이터 분할하기

train = data.query("day<'2018-01-01'")
test = data.query("day>='2018-01-01'")

6.4.2 CATE에 대한 회귀 모델 적합시키기 (cate_pred)
: 추정에는 train data만 사용, test data에서 예측 수행

X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"]
regr_model = smf.ols(f"sales ~ discounts*({'+'.join(X)})",
                     data=train).fit()

cate_pred = (
    regr_model.predict(test.assign(discounts=test["discounts"]+1)) 
    -regr_model.predict(test)
)

* 비교1: 단순 예측 머신러닝 모델 (m1_pred)

from sklearn.ensemble import GradientBoostingRegressor

X = ["month", "weekday", "is_holiday", "competitors_price", "discounts"]
y = "sales"

np.random.seed(1)
ml_model = GradientBoostingRegressor(n_estimators=50).fit(train[X],
                                                          train[y])

ml_pred = ml_model.predict(test[X])

* 비교2: -1과1 사이의 난수 출력 머신러닝 모델 (rand_m_pred)

np.random.seed(123)

test_pred = test.assign(
    ml_pred=ml_pred,
    cate_pred=cate_pred,
    rand_m_pred=np.random.uniform(-1, 1, len(test)),
)

예측값 비교

test_pred[["rest_id", "day", "sales",
           "ml_pred", "cate_pred", "rand_m_pred"]].head()

6.5 모델 분위수에 따른 효과

CATE모델은 어떤 대상이 처치에 더 민감한지 찾는, 개인화에 대한 열망에서 시작되었다.
실험 대상을 민감도가 높은 순서부터 낮은 순서로 나열하는 것은 개인화에 용이하다.
즉, CATE 예측값을 갖고 있다면, 이 값에 따라 실험대상을 순서대로 나열할 수도 있고, 실제 CATE순서와 일치하기를 기대할 수 있을 것
개별 대상 수준에서가 아닌, 순서에 따라 구분된 그룹들은 평가가능할 것

그룹별 인과효과 구하기

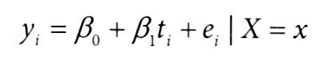
그룹 내에서 T에 대한 Y의 단순회귀분석 수행

그룹 내에서 단순회귀분석을 수행하여 다음과 같이 회귀계수 추정

✅ 커리(curry decorator)
: 부분적으로 적용할 수 있는 함수를 만드는 방법

* dataframe을 유일한 인수로 받는 함수를 생성할 때 유용하다.

from toolz import curry

@curry
def addN(x, N):
	return x+N
ad5 = addN(N=5)
ad13 = addN(N=13)

print(ad5(5))
>>> 10

print(ad13(5))
>>> 18

커리 데코레이터로 인과효과 추정 식을 생성하여 전체 test set에 적용하여 ATE 구하기

from toolz import curry

@curry
def effect(data, y, t):
        return (np.sum((data[t] - data[t].mean())*data[y]) /
                np.sum((data[t] - data[t].mean())**2))
                
effect(test, "sales", "discounts")
>>> 32.16196368039615

하지만 구하고자 하는 것은 이 값이 아니라, 방금 적합된 모델들이 처치에 민감하거나 민감하지 않은 대상을 구분할 수 있는지 여부
→ 모델의 예측값에 따라 데이터를 분위수(quantile)별로 세분화하고 각 분위수에서 효과 추정하기
→ 분위수에서 추정된 효과가 순서대로 '정렬'되었다면, 해당 모델이 CATE를 잘 정렬하는 데 효과적이라 판단 가능

✅ 반응 곡선 형태
: 여기서는 "효과"를 'Y를 T에 회귀한 결과의 기울기 추정값'으로 정의한다.

다른 효과 지표들을 사용할 수도 있다.
ex. 반응 함수가 오목한 형태라고 생각한다면, T가 커질수록 T의 증가율이 동일할 때 Y의 증가폭이 점점 줄어들기에, 효과를 log(T)나 √T에 대한 Y의 회귀 기울기로 정의할 수 있음
ex. Y가 이진 결과라면, 선형회귀분석이 아닌 로지스틱 회귀의 매개변수 추정값을 사용하는 편이 더 적절하다.

→ 핵심은 T가 연속형이면 전체 처치 반응 함수를 단일 효과값으로 '요약'해야 한다는 것

분위수(quantile)별 효과 계산 함수 구현하기

pd.qcut() : 데이터를 q개의 데이터 분포에 따라 균등한 크기의 그룹으로, 즉 분위수(default=10)로 나누기
- 위 함수를 pd.Interval Index로 감싸서 pd.qcut이 반환한 각 그룹의 중간값(.mid) 추출

def effect_by_quantile(df, pred, y, t, q=10):
    
    # 분위수에 대한 파티션 생성
    groups = np.round(pd.IntervalIndex(pd.qcut(df[pred], q=q)).mid, 2) 
    
    return (df
            .assign(**{f"{pred}_quantile": groups}) # '**' 연산자는 딕셔너리 unpack에 사용
            .groupby(f"{pred}_quantile") # 'f(dataframe)'은 df를 input으로 받아 float 출력
            # 분위수별 효과 추정
            .apply(effect(y=y, t=t))) 


effect_by_quantile(test_pred, "cate_pred", y="sales", t="discounts")

[out]
cate_pred_quantile
17.50    20.494153
23.93    24.782101
26.85    27.494156
28.95    28.833993
30.81    29.604257
32.68    32.216500
34.65    35.889459
36.75    36.846889
39.40    39.125449
47.36    44.272549
dtype: float64

참고 - '**'연산자

df = pd.DataFrame({
    'A': [1, 2, 3, 4],
    'B': [5, 6, 7, 8]
})

# 새로운 열의 이름과 값을 지정하는 딕셔너리
new_column_name = 'C'
new_column_values = [10, 20, 30, 40]

# assign을 사용하여 새로운 열 추가
df = df.assign(**{new_column_name: new_column_values})

첫 번째 분위수부터 순서대로 추정 효과가 높아짐을 확인할 수 있다.
→ 이는 CATE 예측이 실제로 효과 순서를 매긴다는 증거가 된다.
앞서 ATE가 32.16이었는데, 중간 정도에 위치하는 6번째 분위수 ATE가 32.21으로, CATE 모델이 실제 CATE의 순서를 매우 잘 반영하고, 정확하게 예측함을 의미한다.

난수 모델의 경우, 그룹별 추정된 효과가 거의 비슷하다. (개인화에 활용 불가)
머신러닝 모델의 경우, 판매 예측이 매우 높거나(=1206.68), 매우 낮을 때(=124.24) 효과가 높게 나타나는 경향이 있다. (개인화에 활용 가능)
- ml 모델이 판매량을 극단적으로 예측할 때, 그 예측이 실제 판매량에 큰 영향을 미친다는 의미
- 그 이유는 ml모델이 판매를 극단적으로 예측할 때에는 작은 변화도 결과에 큰 영향을 미치기 때문
- 판매 예측이 매우 높거나, 매우 낮을 때 더 많은 할인을 제공한다면 결과에 큰 영향을 줄 수 있음
CATE모델의 경우, 분위수에 따라 효과가 증가하는 경향을 보이며, 높은 효과와 낮은 효과를 잘 구분한다.
- CATE 순서 정렬 측면에서, 계단 모양이 가파를수록 더 나은 모델이라는 의미

→ 이렇게 시각적으로 검증할 수도 있지만, 모델 선택(hyper parameter tuning, =특성 선택 feature selection)에 있어서 이상적인 방법은 아님
→ 누적 효과 곡선(cumulative effect curve)을 사용해서 모델의 성능을 하나의 값으로 요약해보자

6.6 누적 효과 곡선

: 그룹을 정의해서 그룹 내 효과를 추정하되, 한 그룹을 다른 그룹 위에 누적하는 형태로 효과를 추정하는 방법

누적 효과 곡선을 생성하는 함수 구현하기

데이터를 점수순으로 정렬
상위 1% 효과 추정
누적 표본에 따른 효과 곡선 생성

: 1%를 추가하여 상위 2%를 계산, 그 후 상위 3%의 효과를 계산하는 식으로 계속 진행

np.linspace(size/steps, size, steps) : size/steps ~ size 까지의 범위를 steps개의 균등한 간격으로 나누기

def cumulative_effect_curve(dataset, prediction, y, t,
                            ascending=False, steps=100):
    size = len(dataset) # 행의 수 계산
    ordered_df = (dataset
                  .sort_values(prediction, ascending=ascending)
                  .reset_index(drop=True)) # prediction 기준 정렬
    
    steps = np.linspace(size/steps, size, steps).round(0) # l
    
    # 단계별로 index가 해당 단계(row) 이하인 subset 선택, 선택된 subset에 대한 처치 효과 계산
    return np.array([effect(ordered_df.query(f"index<={row}"), t=t, y=y)
                     for row in steps])

데이터를 정렬하는 데 사용한 점수가 실제 CATE의 순서를 잘 반영한다면, 해당 곡선은 매우 높게 시작해서 점차 ATE에 수렴하게 된다. (잘못된 모델은 ATE로 빠르게 수렴하거나, 지속해서 그 주변에서 변동할 것)

cumulative_effect_curve(test_pred, "cate_pred", "sales", "discounts")

>> array([49.65116279, 49.37712454, 46.20360341, ..., 32.46981935, 32.33428884,
       32.16196368])

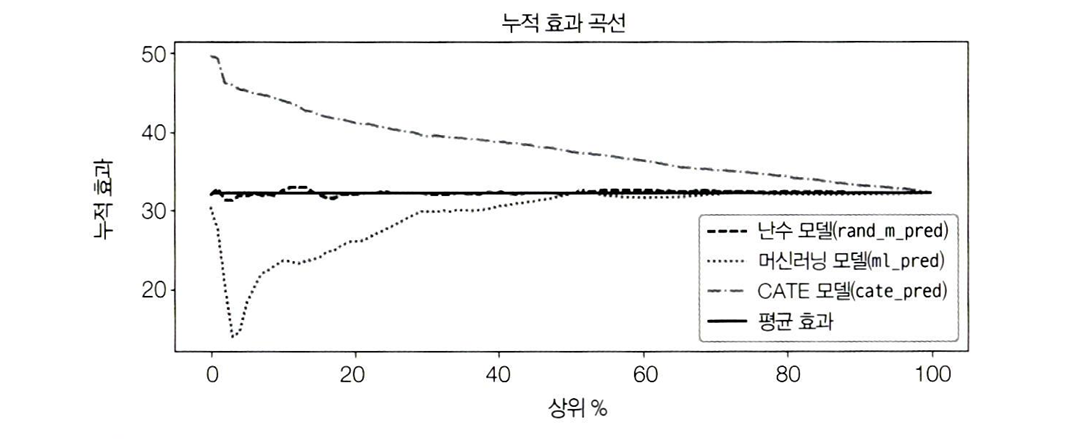
*순서의 비대칭성: 점수의 순서는 대칭적이지 않다.

CATE모델은 매우 높게 시작하여 점차 ATE로 수렴
- 상위20%의 ATE는 약 42, 상위 50%의 ATE는 약 37, 상위 100%의 ATE는 전체 처치효과인 ATE가 된다.
난수 모델은 무작위로 예측하기 때문에 ATE주변에서만 변동
ml모델
- 모델이 가장 효과적인 처치를 잘못된 순서로 예측하여 초기에는 누적효과가 낮게 나타남(ATE 아래에서 시작)
- 순서를 반대로 정렬하는 모델은 ATE아래에서 시작할 것

→ CATE 효과를 누적 효과 곡선을 통해서 추정함으로써 CATE 효과 추정 모델의 정확도를 단일 숫자로 요약할 수 있다.
→ 누적 효과 곡선과 ATE 사이의 면적을 계산하여 모델별로 비교, 면적이 클 수록 좋은 모델로 판단
→ 누적 효과 곡선은 시작 부분이 가장 큰 면적을 차지하는 데, 이 부분에서 표본 크기가 작기에 불확실성이 가장 크다. 이 문제를 해결하기 위해 누적 이득 곡선을 생성해보자.

6.7 누적 이득 곡선

: 누적 효과 곡선과 같은 원리를 적용하되, 각 데이터 포인트에 누적 표본 Ncum / N을 곱하여 누적 이득 곡선 생성하기
→ 좋은 모델의 경우 곡선 시작 부분이 가장 높은 효과를 가지지만, 크기가 작기에 규모가 축소되어 불확실성이 줄어듦

누적 효과 곡선 생성코드에, 매 반복마다 효과에 (row/size) 곱하는 부분 추가해서 누적 이득 곡선 생성하기
(+반복마다 효과에서 정규화 인수(normalizer) 빼기, 정규화 인수인 평균 효과를 빼줌으로써 평균보다 높은지 낮은지 확인할 수 있음)

def cumulative_gain_curve(df, prediction, y, t,
                          ascending=False, normalize=False, steps=100):
    
    effect_fn = effect(t=t, y=y)
    normalizer = effect_fn(df) if normalize else 0
    
    size = len(df)
    ordered_df = (df
                  .sort_values(prediction, ascending=ascending)
                  .reset_index(drop=True))
    
    steps = np.linspace(size/steps, size, steps).round(0)
    effects = [(effect_fn(ordered_df.query(f"index<={row}"))
                -normalizer)*(row/size)  # 정규화 인수(normalizer)빼고, (row/size) 곱해주기
               for row in steps]

    return np.array([0] + effects)


cumulative_gain_curve(test_pred, "cate_pred", "sales", "discounts")

* fklearn causal 모듈에서 라이브러리를 가져와 앞서 다룬 함수들을 처리할 수 있다.

from fklearn.causal.validation.auc import *
from fklearn.causal.validation.curves import *

누적 이득 곡선을 정규화하여 모델의 예측 성능이 평균보다 얼마나 더 나은지, 나쁜지 평가할 수 있다
CATE 순서 측면에서 더 나은 모델은, 곡선과 ATE를 나타내는 점선 사이 면적이 가장 큰 모델이다.

모델 성능을 하나의 값으로 요약하려면, 정규화된 누적 이득 곡선의 값을 합하면 된다. (값이 클수록 좋은 모델)
↔ 누적 이득곡선을 인과모델의 ROC curve로 생각

for m in ["rand_m_pred", "ml_pred", "cate_pred"]:
    gain = cumulative_gain_curve(test_pred, m,
                                 "sales", "discounts", normalize=True)
    print(f"AUC for {m}:", sum(gain))
    
> AUC for rand_m_pred: 6.0745233598544495
> AUC for ml_pred: -45.44063124684 # ml모델은 CATE를 역순으로 정렬하므로 영역이 음수
> AUC for cate_pred: 181.74573239200615

단, 앞서 살펴본 곡선 위의 점은 추정값이며, 참값이 아님을 명심
- 이 회귀계수 추정값은 T와 Y의 관계가 올바르게 정해졌는지에 따라 달라짐
- 무작위 배정되었다 해도, T와 Y의 관계가 로그 함수인데, 선형으로 추정했다면 잘못된 결과가 나올 것
- 효과 함수를 Y~T 가 아닌, Y~log(T) 기울기로 조정
위 곡선은 CATE를 정확히 추정하는 것이 아닌, 순서가 올바른지에 대해서만 관심이 있다.
1. ↔ ROC-AUC가 좋은 모델이라고 해서 모델이 완벽하게 예측한다는 뜻이 아닌 것과 마찬가지
앞서 언급한 방법을 사용하기 위해서는, 교란이 없는 데이터가 필요하다.
1. 편향이 있을 시 IPW의 직교화등을 사용하여 제거 후 이 평가기법을 사용할 수 있다.
2. 하지만 필자는 그렇게 하더라도 교란 있는 데이터에 평가기법을 사용하는 것에 대해 회의적임
3. 실험 데이터를 사용해야 교란 요인의 개입을 걱정할 필요 없이 이질적 효과에 집중할 수 있을 것

→ 필자는 분위수별 효과 그래프와 누적 이득 곡선을 함께 사용하는 방법을 선호한다고 함

분위수별 효과 그래프 : 모델의 보정 정도에 관한 아이디어 제공
- 모델이 잘 보정되었다면, 분위수별 처치 효과가 실제 처치 효과와 잘 맞을 것
- 예측이 높은 분위수에서는 실제 처치효과도 높아야하고, 낮은 분위수에서는 낮아야함
누적 이득 곡선 : CATE의 순서 정렬 정도에 관한 정보 제공
- 상위 1~100%까지의 데이터에 대해 누적 처치 효과를 계산
- 만약 모델이 예측한 순서가 실제 처치 효과의 순서와 잘 맞는다면, 상위 %에서 누적 처치 효과가 점차 증가하는 형태로 나타날 것

→ 예측 모델에서 흔히 사용하는 R^2나 MSE같은 요약 지표는 인과 모델링에 없지만, '목표 변환'이라는 개념이 있다.

6.8 목표 변환

μy는 결과 Y에 대한 모델
τ 는 처치에 대한 모델
분자는 Y와 T의 공분산
분모는 T의 분산
회귀 계수의 공식과 유사하나, 차이점은 기댓값을 사용하는 대신 실험 대상 수준에서 계산되었다는 점

(참고)

위 식에서 흥미로운 점은, Yi'의 기댓값이 타우라는 점

이 목표는 실제 처치효과를 근사한다.
→ 따라서 CATE에 대한 모델이 개별 수준 효과 τi를 예측하는 데 효과적이라면, 이 목표에 대한 모델의 예측 MSE는 작아야 함
이 목표 공식은 T의 평균 값에 가까워질 수록 분모가 0에 가까워지는 경향이 있음
→ 잡음이 커짐

잡음이 커지는 문제 를 해결하기 위해 실험 대상에 가중치 적용하기

* 이러한 가중치를 사용하는 데는 이론적으로 타당한 이유가 있다고 함 (7장. 비모수 이중/편향 제거 ml에서 자세히 다룸)

목표 변수 Yt'를 구하기 (분자 결과 Y의 잔차, 분모 T의 잔차 구하기)

X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"]

y_res = smf.ols(f"sales ~ {'+'.join(X)}", data=test).fit().resid
t_res = smf.ols(f"discounts ~ {'+'.join(X)}", data=test).fit().resid

tau_hat = y_res/t_res

y_res와 t_res로 구한 tau_hat으로 모델별 MSE 계산하기

from sklearn.metrics import mean_squared_error

for m in ["rand_m_pred", "ml_pred", "cate_pred"]:
    wmse = mean_squared_error(tau_hat, test_pred[m],
                              sample_weight=t_res**2)
    print(f"MSE for {m}:", wmse)
    
>>> MSE for rand_m_pred: 1115.803515760459
>>> MSE for ml_pred: 576256.7425385397
>>> MSE for cate_pred: 42.90447405550281

→ CATE를 추정하는 데 사용한 회귀 모델이 다른 두 모델보다 성능이 좋다.
→ ML모델의 목적은 타우가 아닌 Y이기에, 예상할 수 있는 결과

T와 Y가 상관관계가 있을 때, Y를 예측하는 것이 처치효과 순서 정렬이나, 개별 수준 효과 타우를 예측하는 데 효과적이다.
그렇다면, Y를 예측하는 ml모델이 1) 처치효과 순서 정렬과 2) 개별 수준 효과 타우를 예측하는 데 좋은 케이스를 살펴보자.

6.9 예측 모델이 효과 정렬에 좋을 때

:T와 Y가 상관관계가 있다면, Y를 예측하는 것이 처치효과 순서 정렬/타우 예측에 유용할 것
ex. 매출이 높은 날에 사람들이 할인에 더 민감하게 반응하는 경우

*일반적으로 이러한 현상은, 처치 반응 함수가 비선형일 때 발생할 수 있음

6.9.1 예측 모델이 효과 정렬에 좋은 경우

1. 한계 수확 체감 법칙이 발생했을 때

한계 수확 체감(marginal decreasing return)
: 추가적인 투자나 노력이 특정 지점을 넘어서면, 그로부터 얻는 추가적인 이득이 점점 줄어드는 현상
ex. 사업에 자본/노동을 계속 투입하면 처음에는 수익이 많이 증가하나, 어느 정도 이상 투입하게되면 추가 투입에 대한 수익 증가율은 점차 감소하게 됨. 이 개념은 자원 배분과 투자 결정에서 중요한 역할을 한다.

처치 반응 함수가 오목하면, 처치 단위가 늘어날수록 효과가 줄어들게 된다.

즉, 포화점(saturation point)이 존재한다.
ex. 할인율을 100%로 설정하더라도, 판매량은 높아지는 데 한계가 있다.
그 이유는, 생산할 수 있는 양(Y)을 제한하는 요인 때문

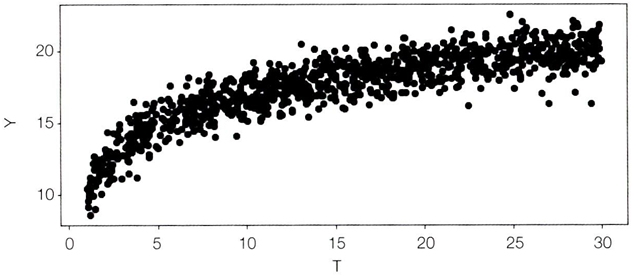
한계 수확 체감의 법칙과 유사한 한계적으로 감소하는 처치 반응 함수의 모습을 통해서, 결과 Y를 잘 예측하는 모델이 CATE를 잘 정렬할 수 있는 이유를 쉽게 알 수 있다.
→ 결과 Y가 높을 수록, 효과가 낮기 때문
→ 예측값의 역순으로 실험 대상을 정렬하면, CATE 순서를 순조롭게 정렬할 수 있을 것

6.9.2 예측 모델이 효과 정렬에 좋을 때

2. 이진 결과일 때

결과 Y가 이진값일 때, Y를 예측하는 모델이 CATE를 잘 정렬하는 데 유용할 수 있다.
이진 결과일 때 E[Y|T]는 0과 1에서 평평해지는 S자 모양이 되기 때문
- S자형 함수는 처음에 천천히 증가하다가 급격히 증가하고, 다시 천천히 증가하는 형태를 가진다.
- 급격히 증가하는 곳 = 분기점

→ 대부분의 비즈니스 적용 사례에서, 데이터는 S자형 함수의 한쪽이나 다른 쪽 끝에 집중된다.

예1. 금융업계(지수함수)

대출 상환(T)이 채무불이행(Y)되는 고객 비율이 극히 낮기 때문에, 이 곡선의 왼쪽 부분에 주로 위치
이런 경우, 고객의 대출 채무불이행(Y)을 예측하는 모델이 있으면, 예측값(Y)이 높은 고객일수록 T에 더 민감하게 반응

상환 비율(T)이 분기점 근처인 고객들은, 상환 비율(T)의 작은 변화에도 채무불이행 가능성(Y)이 크게 변한다. (T의 효과▲)

만약 상환 비율(T)이 50%일 때 채무불이행(Y) 가능성이 급격히 줄어든다고 했을 때,
- 상환 비율이 49%인 고객은 채무불이행(Y) 가능성이 매우 높다.
- 상환 비율이 51%인 고객은 채무불이행(Y) 가능성이 매우 낮다.
- 따라서, 상환 비율(T)이 50% 근처에 있는 고객들은 상환 비율이 조금만 변해도 채무불이행 가능성이 크게 변함
직관적으로, 대출 채무불이행(Y)이 높은 고객은 대출 채무불이행(X)과 상환(T) 사이의 분기점에 가까운 고객들로, 분기점에 있는 고객들에게는 T를 조금만 변화시켜도 결정적인 차이를 만들 수 있을 것

예2. 할인율과 온라인 쇼핑몰 방문자의 구매 전환율

이 경우, S자형 곡선의 오른쪽에 해당된다.
따라서 여기서도 구매 전환(Y)을 예측하는 모델이 있다면, 이 모델이 할인(T)의 효과를 순서대로 정렬하는 데 유용할 것
S자형 곡선의 우측 부분에서 Y가 점진적으로 감소하는 경우 (↔한계 수확 체감의 법칙) 이기 때문에, 전환(Y) 가능성이 높아질수록, 효과(T) 크기는 작아짐

→ 일반적으로 이진 결과라면, 중간값에 가까울수록(↔ E[Y|T] = 50%에 가까울수록) 효과가 증가한다.

✅ 실제 사례: 백신 우선순위 정하기

정책 입안자들은 가장 큰 혜택을 받을 사람들에게 먼저 백신을 접종하고자 했다.
중요한 질문은 '누가 먼저 백신을 맞아야하는가'이기에, 이질적인 처치효과 문제였음
처치효과 T = 사망이나 입원을 방지하는 것
백신 접종 시 사망이나 입원이 가장 많이 감소한 사람들은 노인과 기존 건강 문제가 있는 사람들, 즉 코로나 19 감염시 사망 가능성이 높은 그룹
- 코로나19의 사망률은 50%보다 훨씬 낮아, 로지스틱 함수의 왼쪽 부분에 해당 (채무 불이행 예시와 유사)
- 이 왼쪽 영역에서는, 코로나19에 걸렸을 때 사망할 확률이 높은 사람들에 처치하는 것이 효과적임

처치 반응 함수가 이진 결과처럼 1) 비선형적이거나, 2) 결과가 한계(점진)적으로 감소하는 경우, 예측 모델은 CATE를 잘 정렬할 수 있다.

* 하지만 이것이 가장 좋은 모델임을 의미하지는 않고, CATE 예측을 목적으로 하는 모델보다 성능이 좋다는 것도 아님

처치 효과 '정렬'은 가능하나, '예측'하지는 않는다.
→ 즉, 처치에 대한 민감도에 따라 대상을 정렬하는 게 중요한 문제일 경우에만 적합한 방법이 될 것

* CATE를 정확히 추정하는 것이 결정에 중요하다면 그룹별 추가 효과 추정이 필요하다.

마지막으로 CATE를 결정 과정에 어떻게 활용할 수 있는지 알아보자.

6.10 의사결정을 위한 CATE

처치를 무한정으로 줄 수 있다면, CATE가 양수인 모든 사람들에게 처치하면 된다.
하지만, 처치를 무한정 줄 수 없기에, 추가 규칙을 설정해야 한다.
- 1,000명에게 처치할 수 있다면, CATE순서에 따라 상위 1,000명을 선택하되, 모두 긍정 효과인 경우에만 처치
또한, 처치가 연속형이거나 정렬된 경우에는 상황이 더 복잡해짐
- 누구에게 뿐만 아니라, '어느정도'의 처치를 줄지도 결정해야 함
- 이 문제는 비즈니스 문제마다 최적화해야 할 고유한 처치 반응 함수가 있기에, 사업 특성마다 매우 다를 것

레스토랑 체인에서 매일 얼마나 할인을 제공할지 결정하는 문제로 다시 돌아가보자.

얼마나 할인을 제공할지 결정하는 일 = 어떤 가격을 책정할지 결정하는 것
- Price = Price[base] * (1-Discount))

여기서 만약 문제가 가격 최적화문제라면,

레스토랑의 비용과 수익 함수가 다음과 같은 방정식으로 주어진다고 해보자.
특정 날짜에 사람들이 구매하려는 식사 수 = 해당 날짜에 부과되는 가격에 반비례
- 따라서 τ(Xi)Price 항에서 τ(Xi) 항은 해당 날짜에 고객이 가격 인상에 얼마나 민감한지를 나타냄 (물론 날짜별 특성인 Xi에 따라 달라진다.)
- 즉, τ(Xi)라는 민감도는, 가격이 수요에 미치는 CATE이다.

τ는 곧 수요 곡선의 기울기

수요 곡선에 수익 곡선을 곱하면, 이차 곡선의 형태가 나타난다.
- 수익 = 가격 × 수요

예를 들어, 식사를 만드는데 3달러가 든다고 가정했을 때, 비용은 생산량 q * 3
*여기서 생산량 = 고객 주문량(=수요)

마지막으로 수익과 비용을 얻게되면, 이를 결합하여 가격의 함수로 이익을 계산

다른 τi값에 대한 가격별 이익을 시각화하면, 각기 다른 최적 가격이 산출된다.

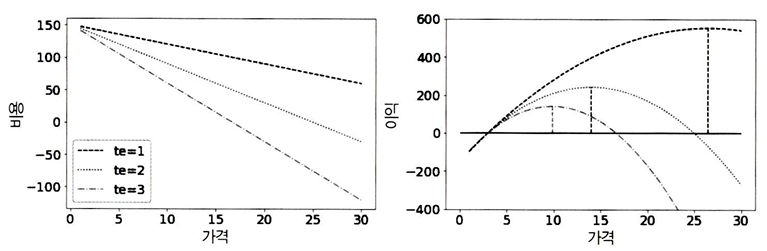
한계 비용을 한계 수익과 동일하게 설정하고, 가격을 분리하면 이윤을 극대화하는 가격의 수치적 해답을 도출할 수 있다.

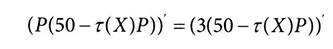
여기에서, 가격이 수요에 미치는 영향인 τ(X)만 유일하게 알려지지 않음
따라서 CATE를 예측하는 모델로 이를 추정할 수 있다면, CATE예측을 최적의 가격으로 변환할 수 있음
- 하지만, CATE예측은 수익 및 비용 곡선의 형태에 따라 달라지며, 이는 비즈니스에 따라 달라짐을 명심

→ 일반적으로 최적화하려는 거의 모든 T에는 상승하는 값(수익)과 하락하는 값(비용)도 있기에, 연속형 처치의 수준을 결정할 때 CATE를 사용하려면, 수익과 비용 두 가지 측면에 처치가 어떤 영향을 미치는지 이해하고 있어야 한다.

✅ 모서리해 (corner solution)
: 드물지만, 비즈니스를 최적화하는 처치 수준이 전혀 없거나, 허용된 최대 수준일 때

EX. 지방 정부가 판매하는 제품의 가격 상한선

이 가격 상한선이 수익을 극대화하는 가격보다 낮다면, 최적의 가격은 정부가 허용하는 최대 가격이 될 것
이런 경우는, 숨겨진 비용을 고려하지 않을 때 모서리해가 발생하는 경우

EX. 교차 판매 이메일 최적화시, 이메일 발송 비용이 미미하므로 모든 사람에게 이메일을 보내야 한다고 생각할 수 있다.

하지만, 고객의 피로도 측면에서 숨겨진 비용이 있음
이런 숨겨진 비용은 고려하지 어렵지만, 존재하지 않는 것은 아님

→ 따라서 숨겨진 비용의 좋은 대체 지표를 찾는 일은 데이터 과학에서 매우 의미 있는 작업이 될 수 있음

※ 추가
https://github.com/CausalInferenceLab/Causal-Inference-with-Python/blob/main/causal-inference-for-the-brave-and-true/18-Heterogeneous-Treatment-Effects-and-Personalization.ipynb

Causal-Inference-with-Python/causal-inference-for-the-brave-and-true/18-Heterogeneous-Treatment-Effects-and-Personalization.ipyn

Causal Inference for The Brave and True 책의 한국어 번역 자료입니다. - CausalInferenceLab/Causal-Inference-with-Python

github.com

From Predictions to Causal Inference
: ML을 유용하게 사용하려면, ML로 해결하고자 하는 모든 문제를 E[Y|X]로 추정하는 것이 핵심인 예측 문제로 프레임화 해야 한다.
✅ EX. 고객별 수익성 예측 → 고객별 특징인 E[순가치|나이,소득,지역]을 통해서 고객별 수익성 예측

실질적으로 어떤 액션을 취해야하는가에 대한 답을 준다. → 수익성이 낮은 고객과는 거래하지 않고, 수익성이 높은 고객과 거래하는 데에 노력을 집중할 수 있도록 도울 수 있다.
하지만 여전히 그것만으로 수익성을 실질적으로 증가시키거나, 감소시킬 수 없다.

인과 추정을 넘어, "최적화"하기

사실 많은 경우 기업들은 고객의 수익성을 높이기 위한 레버들을 갖고 있고, 레버에는 고객 서비스, 가격할인, 마케팅 등이 있다.
이러한 레버, 즉 데이터 "생성" 프로세스에 데이터 과학자가 포함되어 영향을 줄 수 있다.
다른 중간 지표(비즈니스 지표)를 최적화하기 위해 "어떤" 조치를 취하는 것이 최선인지, 어떤 개입을 해야하는지 대답할 수 있어야 한다.
즉, 수동적인 관찰자가 아니기에, 전체 그림을 파악해야 하고, E[Y|X] 추정만으로는 파악이 불가하여 인과추론을 시작하게 된다.
조건부 기댓값에 다른 조각을 추가해야 하고, 그 부분이 바로 데이터 생성 프로세스에 대한 데이터 과학자의 참여를 모델링하는 부분이 된다. 여기서 조각은 "처치".

E[Y|X,T]를 모델링하기 위해서는 맥락 또는 외생적 특징인 X와 처치 T를 구분해야 한다.

X는 제어권이 없고, T는 어떤 값을 취할지 결정 가능
정해진 X 컨텍스트에서 T와 Y의 인과 관계를 추정하게 되면, Y를 최적화하는 것은 T를 최적의 방법으로 설정하는 문제로 "구체화"된다.

<1장>에서 집중한 부분

처치가 양수인지, 강한지, 없는지에 대한 답변에 집중 (ex. 교육에 투자하는 것이 좋은 생각인가?)
1장에서 X의 역할은 두 개
1. X는 교란 요인을 포함할 수 있으며, 포함될 경우 X에 대해 조정해야지만 인과 효과를 '식별'할 수 있다.
2. X는 인과 추정의 분산을 감소시키는 역할을 할 수 있다.

→ 컨텍스트 피처가 되는 X는 개인 각각을 "정의"하는 역할을 하며, 이에 따라 T에 다르게 반응할 것이다.
→ 따라서 T를 개인화하여 T에 가장 잘 반응하는 유닛에만 제공하고자 한다.

저작자표시

'데이터 분석 > 인과추론' 카테고리의 다른 글

[8-1] 실무로 통하는 인과추론 with 파이썬 - 8장. 이중차분법 (0)	2024.06.11
[7] 실무로 통하는 인과추론 with 파이썬 - 7장. 메타 러너 (0)	2024.06.02
[5-2] 실무로 통하는 인과추론 with 파이썬 - 5장. 성향점수 (0)	2024.05.18
[5-1] 실무로 통하는 인과추론 with 파이썬 - 5장. 성향점수 (0)	2024.05.14
[4-2] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 (0)	2024.05.12

'데이터 분석/인과추론' Related Articles

Comments

LITTLE BY LITTLE

[6] 실무로 통하는 인과추론 with 파이썬 - 6장. 이질적 처치효과 본문

[6] 실무로 통하는 인과추론 with 파이썬 - 6장. 이질적 처치효과

'데이터 분석 > 인과추론' 카테고리의 다른 글

티스토리툴바