| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 컨브넷
- ARIMA
- 데이터 정합성
- WITH CUBE
- 캐글 신용카드 사기 검출
- sql
- 리프 중심 트리 분할
- tableau
- splitlines
- ImageDateGenerator
- 캐글 산탄데르 고객 만족 예측
- 스태킹 앙상블
- 마케팅 보다는 취준 강연 같다(?)
- 그로스 마케팅
- 인프런
- DENSE_RANK()
- XGBoost
- 그로스 해킹
- 3기가 마지막이라니..!
- 데이터 핸들링
- 그룹 연산
- 데이터 증식
- lightgbm
- Growth hacking
- pmdarima
- 부트 스트래핑
- 분석 패널
- python
- WITH ROLLUP
- 로그 변환
- Today
- Total
LITTLE BY LITTLE
[13] 파이썬 머신러닝 완벽 가이드 - 7. 군집화 (평균 이동, GMM, DBSCAN, 고객 세그먼테이션 실습) 본문
[13] 파이썬 머신러닝 완벽 가이드 - 7. 군집화 (평균 이동, GMM, DBSCAN, 고객 세그먼테이션 실습)
위나 2022. 9. 17. 14:357. 군집화
K-평균 알고리즘 이해군집 평가- 평균 이동 (Mean shift)
- GMM(Gaussian Mixture Model)
- DBSCAN
- 군집화 실습 - 고객 세그먼테이션
- 정리
- 차원 축소
- LDA (Linear Discriminant Anlysis)
- SVD (Singular Value Decomposition)
- NMF (Non-Negative Matrix Factorization)
- 정리
- 회귀
- 다항 회귀와 과(대)적합/과소적합 이해
- 규제 선형 모델 - 릿지, 라쏘, 엘라스틱 넷
- 로지스틱 회귀
- 회귀 트리
- 회귀 실습 - 자전거 대여 수요 예측
- 회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
- 정리
- 텍스트 분석
- 텍스트 분석 이해
- 텍스트 사전 준비 작업(텍스트 전처리) - 텍스트 정규화
- Bag of Words - BOW
- 텍스트 분류 실습 - 20 뉴스그룹 분류
- 감성 분석
- 토픽 모델링 - 20 뉴스그룹
- 문서 군집화 소개와 실습 (Opinion Review 데이터셋)
- 문서 유사도
- 한글 텍스트 처리 - 네이버 영화 평점 감성 분석
- 텍스트 분석 실습 - 캐글 mercari Price Suggestion Challenge
- 정리
- 추천 시스템
- 추천 시스템의 개요와 배경
- 콘텐츠 기반 필터링 추천 시스템
- 최근접 이웃 협업 필터링
- 잠재요인 협업 필터링
- 콘텐츠 기반 필터링 실습 - TMDV 5000 영화 데이터셋
- 아이템 기반 최근접 이웃 협업 필터링 실습
- 행렬 분해를 이용한 잠재요인 협업 필터링 실습
- 파이썬 추천 시스템 패키지 - Surprise
- 정리
7-3. 평균 이동(Mean shift)
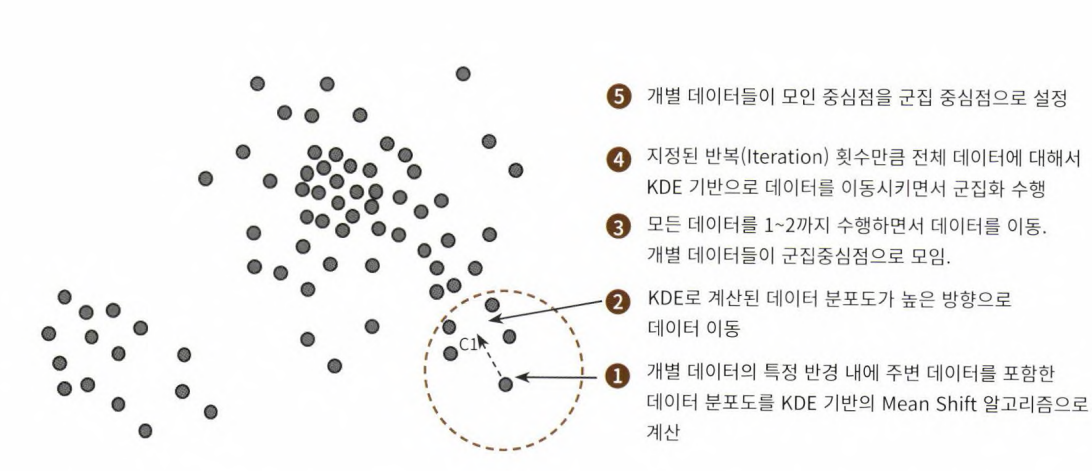

- k-평균과 유사하게 군집의 중심으로 지속적으로 움직이면서 군집화를 수행하는 방법, 차이점은 평균 거리 중심으로 이동하는 것이 아니라, 중심을 데이터가 모여있는 '밀도가 가장 높은 곳'으로 이동시킨다.
- 확률 밀도 함수(pdf) 이용
- KDE(Kernel Density Estimation, 대표적인 커널 함수로서 가우시안 분포 함수가 사용됨)를 이용한다.
- 주변 데이터와의 거리 값은 kde 함수 값으로 입력, 그 반환값을 현재 위치에서 업데이트하면서 이동하는 방식
- 과적합을 피하기 위해서 KDE의 대역 폭 h를 계산하는 것은 KDE 기반의 평균 이동(Mean Shift) 군집화에서 매우 중요하다.
- 군집의 개수를 정하지 안혹, 오직 대역폭의 크기에 따라 군집화를 수행
- 사이킷런의
- MeanShift 클래스
- 중요 파라미터는 bandwidth (=ked의 대역폭 h)
- 최적의 대역폭 계산 함수 estimate_bandwidth
- MeanShift 클래스
make_blobs()의 cluster_st를 0.7로 정한 3개의 군집 데이터에 대해 bandwidth를 0.8로 설정한 평균 이동 군집화 알고리즘
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.cluster import MeanShift
X,y = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.7, random_state=0)
meanshift = MeanShift(bandwidth=0.8)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))[Out]
cluster labels 유형: [0 1 2 3 4 5]# 위에서는 군집이 6개로, 지나치게 세분화되어 군집화되었다. bandwidth를 높인 1.0으로 설정하여 MeanShift를 수행해보자
meanshift = MeanShift(bandwidth=1)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))[Out]
cluster labels 유형: [0 1 2]=> bandwidth 값을 작게 할수록 군집 개수가 많아진다.
estimate_bandwidth()의 파라미터로 피처 데이터셋을 입력하여 최적화된 bandwidth를 찾아보자
from sklearn.cluster import estimate_bandwidth
bandwidth = estimate_bandwidth(X)
print('bandwidth값:', round(bandwidth,3))[Out]
bandwidth값: 1.816import pandas as pd
clusterDF = pd.DataFrame(data=X, columns=['ftr1','ftr2'])
clusterDF['target'] = y
# estimate_bandwidth()로 최적의 bandwidth 계산
best_bandwidth = estimate_bandwidth(X)
meanshift = MeanShift(bandwidth = best_bandwidth)
cluster_labels = meanshift.fit_predict(X)
print('cluster labels 유형:', np.unique(cluster_labels))[Out]
cluster labels 유형: [0 1 2]=> 3개의 군집이 best
구성된 3개의 군집을 시각화해보자. (k-means와 마찬가지로 cluster_centers_속성으로 군집 중심좌표를 표시할 수 있다.
import matplotlib.pyplot as plt
%matplotlib inline
clusterDF['meanshift_label'] = cluster_labels
centers = meanshift.cluster_centers_
unique_labels = np.unique(cluster_labels)
markers=['o','s','^','x','*']
for label in unique_labels:
label_cluster = clusterDF[clusterDF['meanshift_label']==label]
center_x_y = centers[label]
#군집별로 다른 마커로 산점도 적용
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k', marker=markers[label])
#군집별 중심 표현
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='gray', alpha=0.9, marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k', edgecolor='k', marker='$%d$' % label)
plt.show()[Out]

target값과 군집 label 값을 비교해보자.
print(clusterDF.groupby('target')['meanshift_label'].value_counts())[Out]
target meanshift_label
0 0 67
1 1 67
2 2 66
Name: meanshift_label, dtype: int64=> Target과 label의 값이 1:1로 잘 매칭되었다.
평균이동(Mean-Shift)
1. 장점은 데이터셋을 특정 형태로 가정하건, 분포 기반 모델로 특정하지 않아 유연한 군집화 가능
2. 수행 시간이 오래걸리고, band-width의 크기에 따른 군집화 영향도가 크다는 것이 단점
3. 분석 업무 기반 데이터셋보다는 컴퓨터 비전 영역에서 많이 사용됨 (ex.이미지에서 특정 개체 구분, 움직임 추적)
7-3. GMM(Gaussian Mixture Model)


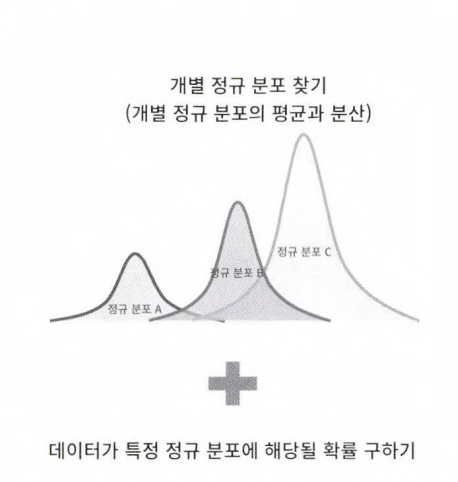
- 군집화를 적용하고자 하는 데이터가 여러 개의 가우시안 분포를 가진 데이터 집합들이 섞여 생성된 것이라는 가정하에 군집화를 수행하는 방식
- 여러 개의 정규 분포 곡선을 추출하고, 개별 데이터가 이 중 어떤 정규분포에 속하는지 결정하는 방식
- 모수 추정
- 개별 정규분포의 평균과 분산
- 각 데이터가 어떤 정규분포에 해당되는지의 확률
- 위의 모수추정을 이해 EM(Expectation and Maximization) 방법 적용 - GaussianMixture 클래스
GMM을 이용해 붓꽃 데이터셋을 군집화해보자
- GaussianMixture 객체의 가장 중요한 초기화 파라미터는 n_components(=gaussian mixture 모델의 총 개수)
- k-means의 n_clusters와 같이 군집의 개수를 정하는 데 중요한 역할을 수행한다.
- n_components를 3으로 설정하고, GaussianMixture로 군집화를 수행해보자.
- GaussianMixture클래스는 sklearn.mixture 패키지에 위치해있다.
- GaussianMixture 객체의 fit()과 predict()를 수행해 군집 결정
- 그 후 irisDF DataFrame에 'gmm_cluster'컬럼명으로 저장하고, 타깃별로 군집이 어떻게 매핑되었는지 확인해보자.
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3, random_state=0).fit(iris.data)
gmm_cluster_labels = gmm.predict(iris.data)
# 군집화 결과를 irisDF의 'gmm_cluster' 컬럼명으로 저장
irisDF['gmm_cluster'] = gmm_cluster_labels
irisDF['target'] = iris.target
# target 값에 따라 gmm_cluster 값이 어떻게 매핑되었는지 확인
iris_result = irisDF.groupby(['target'])['gmm_cluster'].value_counts()
print(iris_result)[Out]
target gmm_cluster
0 0 50
1 2 45
1 5
2 1 50
Name: gmm_cluster, dtype: int64=>n target0은 cluster0에, target2는 cluster1에 잘 매핑되었다.
=> 반면에, target1은 1에 5개(10%) 밖에 매핑되지 않음
=> k-means 보다 효과적인 분류결과, 비교해보자
# k-means와 비교
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0).fit(iris.data)
kmeans_cluster_labels = kmeans.predict(iris.data)
irisDF['kmeans_cluster'] = kmeans_cluster_labels
iris_result = irisDF.groupby(['target'])['kmeans_cluster'].value_counts()
print(iris_result)[Out]
target kmeans_cluster
0 1 50
1 0 48
2 2
2 2 36
0 14
Name: kmeans_cluster, dtype: int64=> 이는 붓꽃 데이터셋이 K-MEANS보다 GMM 군집화에 더 효과적이라는 의미
=> K-MEANS는 평균 거리 중심으로 이동하면서 군집화를 수행하는 방식이라서, 개별 군집 내의 데이터가 원형으로 흩어져있는 경우 효과적
GMM과 K-평균의 비교
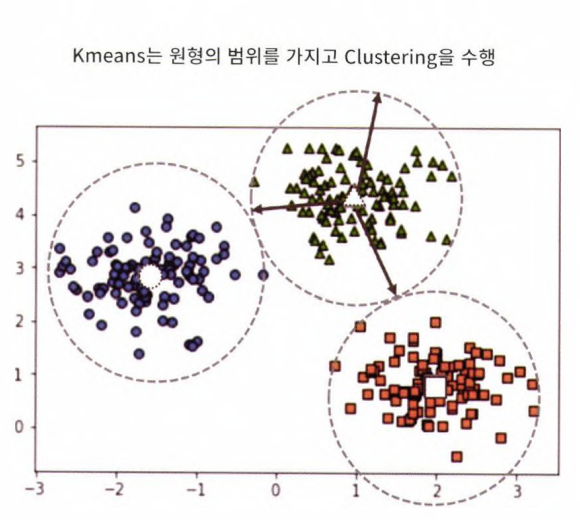
- Kmeans는 원형의 범위에서 군집화를 수행한다. 데이터셋이 원형의 범위를 가질수록 효율이 높아짐
- cluster_std를 0.5로 설정해서 데이터를 뭉치게 유도한 데이터셋에 kmeans를 적용해보자. (이렇게 std를 작게 설정하면 데이터가 원형 형태로 분산될 수 있다.
- 반대로 Kmeans는 데이터가 길쭉한 타원형으로 늘어선 경우 군집화를 잘 수행하지 못한다.
make_blob()의 데이터를 변환해 데이터셋을 만들어 군집화해보자.
군집 시각화 함수 visualize_cluster_plot 함수를 만들어놓자.
- clusterobj : 군집 수행 객체 (군집화를 완료한 객체)
- dataframe : 피처 데이터셋과 label값을 가진 df
- label_name : df 내의 군집화 label 컬럼 명
- iscenter : Cluster 객체가 군집 중심 좌표를 제공하면 True, 그렇지않으면 False
def visualize_cluster_plot(clusterobj, dataframe, label_name, iscenter=True):
# 군집별 중심 위치: K-Means, Mean Shift 등
if iscenter:
centers = clusterobj.cluster_centers_
# Cluster 값 종류
unique_labels = np.unique(dataframe[label_name].values)
markers=['o', 's', '^', 'x', '*']
isNoise=False
for label in unique_labels:
# 군집별 데이터 프레임
label_cluster = dataframe[dataframe[label_name]==label]
if label == -1:
cluster_legend = 'Noise'
isNoise=True
else:
cluster_legend = 'Cluster '+str(label)
# 각 군집 시각화
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], s=70,
edgecolor='k', marker=markers[label], label=cluster_legend)
# 군집별 중심 위치 시각화
if iscenter:
center_x_y = centers[label]
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=250, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k',\
edgecolor='k', marker='$%d$' % label)
if isNoise:
legend_loc='upper center'
else:
legend_loc='upper right'
plt.legend(loc=legend_loc)
plt.show()from sklearn.datasets import make_blobs
# make_blobs()로 300개의 데이터셋, 3개의 군집 세트 clsuter_std=0.5를 만듦
X, y = make_blobs(n_samples=300, n_features=2, centers=3, cluster_std=0.5, random_state=0)
# 길게 늘어난 타원형의 데이터셋을 생성하기 위해 변환함
transformation = [[0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation)
# feature 데이터셋과 make_blobs()의 y 결괏값 df로 저장
clusterDF = pd.DataFrame(data=X_aniso, columns=['ftr1','ftr2'])
clusterDF['target'] = y
# 생성된 데이터셋을 target별로 다른 마커로 표시해 시각화
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)[Out]

# 3개의 군집 기반 Kmeans를 X_aniso 데이터셋에 적용
kmeans = KMeans(3, random_state=0)
kmeans_label = kmeans.fit_predict(X_aniso)
clusterDF['kmeans_label'] = kmeans_label
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_label', iscenter=True)[Out]

=> KMeans로 군집화를 수행할 경우, 주로 원형 영역 위치로 개별 군집화가 되면서 원하는 방향으로 구성되지 않음을 알 수 있다.
이번에는 같은 데이터를 GMM으로 군집화를 수행해보자.
# 3개의 n_components 기반 GMM을 X_aniso 데이터셋에 적용
gmm = GaussianMixture(n_components=3, random_state=0)
gmm_label = gmm.fit(X_aniso).predict(X_aniso)
clusterDF['gmm_label'] = gmm_label
# GaussianMixture는 cluster_centers_ 속성이 없으므로 iscenter을 False로 설정
visualize_cluster_plot(gmm, clusterDF, 'gmm_label', iscenter=False)[Out]

=> GMM 수행 결과, 데이터가 분포된 방향에 따라 정확하게 군집화되었음을 알 수 있다.
=> K-평균과 다르게 군집의 중심 좌표를 구할 수 없기 때문에, 군집 중심 표현이 visualize_cluster_plot()에서 시각화되지 않는다.
make_blobs()의 target 값과 KMeans, GMM의 군집 label값을 서로 비교해 얼마나 군집화 효율차이가 발생하는지 확인해보자.
print('### KMeans Clustering ###')
print(clusterDF.groupby('target')['kmeans_label'].value_counts())
print('\n### Gaussian Mixture Clustering ###')
print(clusterDF.groupby('target')['gmm_label'].value_counts())[Out]
### KMeans Clustering ###
target kmeans_label
0 2 73
0 27
1 1 100
2 0 86
2 14
Name: kmeans_label, dtype: int64
### Gaussian Mixture Clustering ###
target gmm_label
0 2 100
1 1 100
2 0 100
Name: gmm_label, dtype: int64=> KMeans의 경우 군집 1번만 완벽하게 매핑되었지만, 나머지군집의 경우 어긋나는 경우가 발생하고있다.
=> 반면에 GMM은 군집이 target값과 잘 매칭되었다.
=> 이처럼 GMM의 경우, Kmeans보다 유연하게 다양한 데이터셋에 잘 적용될 수 있다. 하지만 시간이 오래걸린다는 단점
7-5. DBSCAN
- 밀도 기반 군집화의 대표적인 알고리즘 DBSCAN(Density Based Spatial Clustering Of Applications With Noise)
- 간단하고 직관적인 알고리즘이지만, 데이터 분포가 기하학적으로 복잡하더라도 효과적인 군집화가 가능
- 내부의 원 모양과 외부의 원 모양 형태의 분포를 가진 데이터셋을 군집화한다고 가정할 때, 앞서 소개된 방법은 모두 효과적인 군집화를 수행하기 힘든 반면, DBSCAN은 밀도차이를 기반으로 해서 군집화를 잘 수행할 수 있다.
- 구성하는 가장 중요한 파라미터는 입실론(=주변 영역)과 최소 데이터 개수
- epsilon : 입실론 주변 영역, 개별 데이터를 중심으로 입실론 반경을 가지는 원형의 영역
- min points : 개별 데이터의 입실론 주변 영역에 포함되는 타 데이터의 개수
- 입실론 주변 영역 내에 포함되는 최소 데이터 개수를 충족시키는지 여부에 따라 데이터포인트를 다음과 같이 정의
- 핵심 포인트 Core point : 주변 영역 내에 최소 데이터 개수 이상의 타 데이터를 갖고 있음
- 이웃 포인트 Neighbor point : 주변 영역 내에 위치한 타 데이터를 의미
- 경계 포인트 Border point : 주변 영역 내에 핵심포인트를 이웃포인트로 갖고 있음
- 잡음 포인트 Noise point : 1,3 둘다 해당 안될 경우
- DBSCAN 클래스
- DBSCAN 알고리즘 지원, 주요 초기화 파라미터는
- eps : 입실론 주변 영역의 반경을 의미
- min_samples : 핵심 포인트가 되기 위해 입실론 주변 영역 내에 포함되어야할 데이터의 최소 개수(자신의 데이터 포함, 위에서 설명한 min points +1)
- DBSCAN 알고리즘 지원, 주요 초기화 파라미터는

붓꽃 데이터로 DBSCAN 실습
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.6, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)[Out]
target dbscan_cluster
0 0 49
-1 1
1 1 46
-1 4
2 1 42
-1 8
Name: dbscan_cluster, dtype: int64=> 특이하게 -1이 군집 레이블로 존재, 군집레이블이 -1인 것은 노이즈에 속하는 군집을 의미한다.
=> TARGET값의 유형이 3가지인데, 군집이 0과1로 2개가 되었으나, 군집화 효율이 떨어진다는 의미는 아니며, DBSCAN에서 군집의 개수는 자동 지정되어 지정하는 것이 의미가 없다.
=> 특히 붓꽃 데이터셋은 군집을 3개로 하는 것보다 2개로 하는 것이 더 효율이 좋은 면이 있음
DBSCAN으로 군집화 데이터셋을 2차원 평면에서 표현하기 위해 PCA를 이용해 2개의 피처로 압축 변환한 뒤, 앞 예제에서 사용한 visualize_cluster_plot() 함수를 이용해 시각화해보자.
from sklearn.decomposition import PCA
# 2차원으로 시각화하기 위해 PCA n_components=2로 피처 데이터셋 변환
pca = PCA(n_components=2, random_state=0)
pca_transformed = pca.fit_transform(iris.data)
#visualize_cluster_s3() 함수는 ftr1, ftr2칼럼을 좌표에 표현하므로 pca 변환값을 해당 컬럼으로 생성
irisDF['ftr1'] = pca_transformed[:, 0]
irisDF['ftr2'] = pca_transformed[:, 1]
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)[Out]

=> 별표로 표현된 값은 노이즈이다. pca로 2차원으로 표현하면 이상치인 노이즈 데이터가 명확히 드러남
- DBSCAN을 적용할 때는 특정 군집 개수로 군집을 강제하지 않는 것이 좋다.
- DBSCAN 알고리즘에 적절한 eps와 min_samples 파라미터를 통해 최적의 군집을 찾는 것이 중요
- 일반적으로 eps 값을 크게하면 반경이 커져 포함하는 데이터가 많아지므로, 노이즈 데이터 개수가 작아진다.
- min_samples를 크게 하면 주어진 반경 내에서 더 많은 데이터를 포함시켜야 하므로 노이즈 데이터 개수가 커지게 된다. 데이터 밀도가 커져야하는데, 매우 촘촘한 데이터 분포가 아닌 경우 노이즈로 인식하기 때문
eps를 0.6에서 0.8로 증가시키고, 노이즈 데이터수가 줄어드는지 확인해보자.
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.8, min_samples=8, metric='euclidean')
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)[Out]
target dbscan_cluster
0 0 50
1 1 50
2 1 47
-1 3
=> 기존에 eps가 0.6일 때 노이즈로 분류된 데이터셋은 eps 반경이 커지면서 clsuter1에 소속되었다.
이번에는 eps를 기존 0.6으로 유지하고, min_samples를 16으로 늘려보자. (노이즈가 늘어남)
(바로 위 예제 코드에서 DBSCAN의 초기화 파라미터 값만 다음과 같이 변경하면 된다.)
dbscan = DBSCAN(eps=0.6, min_samples=16, metric='euclidean')
#나머지 코드는 동일
dbscan_labels = dbscan.fit_predict(iris.data)
irisDF['dbscan_cluster'] = dbscan_labels
irisDF['target'] = iris.target
iris_result = irisDF.groupby(['target'])['dbscan_cluster'].value_counts()
print(iris_result)
visualize_cluster_plot(dbscan, irisDF, 'dbscan_cluster', iscenter=False)[Out]
target dbscan_cluster
0 0 48
-1 2
1 1 44
-1 6
2 1 36
-1 14
DBSCAN 적용하기 - make_circles() 데이터셋
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, shuffle=True, noise=0.05, random_state=0, factor=0.5)
# noise는 노이즈 데이터셋 비율, factor는 외부 원과 내부 원의 scale 비율
clusterDF = pd.DataFrame(data=X, columns=['ftr1', 'ftr2'])
clusterDF['target']= y
visualize_cluster_plot(None, clusterDF, 'target', iscenter=False)[Out]

먼저 k-평균으로 make_circles() 데이터셋을 군집화해보자.
# KMeans로 make_circles() 데이터셋을 군집화 수행
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2, max_iter=1000, random_state=0)
kmeans_labels = kmeans.fit_predict(X)
clusterDF['kmeans_cluster'] = kmeans_labels
visualize_cluster_plot(kmeans, clusterDF, 'kmeans_cluster', iscenter=True)[Out]

=> 위, 아래 군집 중심을 기반으로 위와 아래 절반으로 군집화되었다.
=> 거리 기반 군집화로는 위와 같이 데이터가 특정한 형태로 지속해서 이어지는 부분을 찾아내기 어렵다.
GMM을 적용해보자.
# GMM으로 make_circles() 데이터셋을 군집화 수행
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2, random_state=0)
gmm_label = gmm.fit(X).predict(X)
clusterDF['gmm_cluster'] = gmm_label
visualize_cluster_plot(gmm, clusterDF, 'gmm_cluster', iscenter=False)[Out]

=> GMM도 내부와 외부의 원형으로 구성된 복잡한 형태의 데이터셋에서는 군집화가 원하는 방향대로 되지 않았다.
DBSCAN으로 군집화를 적용해보자.
#DBSCAN으로 make_circles() 데이터셋 군집화 수행
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps=0.2, min_samples=10, metric='euclidean')
dbscan_labels = dbscan.fit_predict(X)
clusterDF['dbscan_cluster'] = dbscan_labels
visualize_cluster_plot(dbscan, clusterDF, 'dbscan_cluster', iscenter=False)[Out]

7-6. 군집화 실습 - 고객 세그먼테이션

http://archive.ics.uci.edu/ml/datasets/online+retail
UCI Machine Learning Repository: Online Retail Data Set
Online Retail Data Set Download: Data Folder, Data Set Description Abstract: This is a transnational data set which contains all the transactions occurring between 01/12/2010 and 09/12/2011 for a UK-based and registered non-store online retail. Data Set Ch
archive.ics.uci.edu
import pandas as pd
import datetime
import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
retail_df = pd.read_excel('/content/Online Retail.xlsx')
retail_df.head()[Out]

- Invoice No : 주문번호, 'c'로 시작하는건 취소 주문
- StockCode : 제품 코드(Item code)
- Description : 제품 설명
- Quantity : 주문 제품 건수
- Invoice Date : 주문 일자
- UnitPrice : 제품 단가
- Customer ID : 고객 번호
- Country : 주문 고객의 국적
데이터 전체 건수, 컬럼 타입, Null 개수 확인
retail_df.info()[Out]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 541909 entries, 0 to 541908
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 InvoiceNo 541909 non-null object
1 StockCode 541909 non-null object
2 Description 540455 non-null object
3 Quantity 541909 non-null int64
4 InvoiceDate 541909 non-null datetime64[ns]
5 UnitPrice 541909 non-null float64
6 CustomerID 406829 non-null float64
7 Country 541909 non-null object
dtypes: datetime64[ns](1), float64(2), int64(1), object(4)
memory usage: 33.1+ MB=> 전체 데이터는 541,909개
=> customer ID 컬럼의 NULL 개수가 많음
=> 그외에 컬럼 데이터에도 오류 데이터 존재
사전 정제 작업
1. customer ID의 Null데이터 삭제
2. 오류 데이터 삭제 - 대표적 오류데이터는 Quantity 또는 UnitPrice가 0보다 작은 경우, Quantity가 0보다 작은 경우는 반환을 뜻하는 값이고, 이 경우 InvoiceNo 앞자리는 'C'(취소)로 되어있다. 분석의 효율성을 위해 이러한 데이터도 삭제
retail_df = retail_df[retail_df['Quantity']>0]
retail_df = retail_df[retail_df['UnitPrice']>0]
retail_df = retail_df[retail_df['CustomerID'].notnull()]
print(retail_df.shape)
retail_df.isnull().sum()[Out]
(397884, 8)
InvoiceNo 0
StockCode 0
Description 0
Quantity 0
InvoiceDate 0
UnitPrice 0
CustomerID 0
Country 0
dtype: int64=> 전체 데이터가 514,909개에서 397,884개로 줄고, NULL값이 삭제되었다.
사전정제 작업 마지막으로 Country 칼럼에서 주요 주문 고객인 영국만 다루기위해 나머지 국가를 제외해주자
retail_df['Country'].value_counts()[:5][Out]
United Kingdom 354321
Germany 9040
France 8341
EIRE 7236
Spain 2484
Name: Country, dtype: int64영국만 남기고 제외
retail_df = retail_df[retail_df['Country']=='United Kingdom']
print(retail_df.shape)[Out]
(354321, 8)RFM(Recency, Frequency, Monetary) 기반 데이터 가공
- Unit Price * Quantity 두 컬럼 곱해서 '주문 금액(sale_amount)' 데이터 만들기
- Customer No 컬럼을 float형에서 int형으로 변경
retail_df['sale_amount'] = retail_df['Quantity']*retail_df['UnitPrice']
retail_df['CustomerID']= retail_df['CustomerID'].astype(int)위 데이터는 개인고객과 소매점 주문이 함께 포함되어있다.
top-5 주문 건수와 주문 금액을 가진 고객 데이터를 추출해보자.
print(retail_df['CustomerID'].value_counts().head(5))
print(retail_df.groupby('CustomerID')['sale_amount'].sum().sort_values(ascending=False)[:5])[Out]
17841 7847
14096 5111
12748 4595
14606 2700
15311 2379
Name: CustomerID, dtype: int64
CustomerID
18102 259657.30
17450 194550.79
16446 168472.50
17511 91062.38
16029 81024.84
Name: sale_amount, dtype: float64=> 몇몇 특정 고객이 많은 주문 건수와 주문 금액을 갖고있다.
** 분석 목적을 위해 데이터 구조 변경
위 데이터셋은 InvoiceNo + StockCode 레벨의 식별자로 되어있다.
InvoiceNo + StockCode로 Group by를 수행하면 거의 1에 가깝게 유일한 식별자 레벨이 됨을 알 수 있다.
retail_df.groupby(['InvoiceNo', 'StockCode'])['InvoiceNo'].count().mean()[Out]
1.028702077315023=> RFM 기반 고객 세그먼테이션은 '고객 레벨'로 주문 기간/횟수/금액 데이터를 기반으로 해야한다.
=> 따라서 주문번호+상품번호 기준의 데이터를 고객 기준 Recency, Frequency, Monetary value 데이터로 변경하자.
- 변경하기 위해서는 InvoiceNo 기준 데이터를 개별 고객 기준 데이터로 Groupby 해야한다.
- InvoiceNo 기준 retail_df DataFrame에 groupby('CustomerID')를 적용해 CustomerID 기준으로 DataFrame을 새롭게 생성하자.
- DataFrame에 groupby를 호출해 반환된 DataFrameGroupby 객체에 agg()를 이용해서 한번에 연산을 수행하자.
- Frequency는 'CustomerID'로 groupby()해서 'InvoiceNo'의 count() aggregation으로 구함
- Monetary value는 'CustomerID'로 groupby()해서 'sale_amount'의 sum() aggregation으로 구함
- Recency의 경우 두 번의 가공 작업을 수행
- 'Customer ID'로 groupby()해서 'InvoiceDate' 컬럼의 max()로 고객별 가장 최근 주문일자를 먼저 구한 뒤, 추후에 가공 작업 수행
aggregations = {
'InvoiceDate' : 'max',
'InvoiceNo' : 'count',
'sale_amount' : 'sum'
}
cust_df = retail_df.groupby('CustomerID').agg(aggregations)
# groupby 된 결과 컬럼 값을 Recency, Frequency, Monetary로 변경
cust_df = cust_df.rename(columns = {'InvoiceDate' : 'Recency',
'InvoiceNo' : 'Frequency',
'sale_amount' : 'Monetary'})
cust_df = cust_df.reset_index()
cust_df.head()[Out]

Recency 컬럼 추가 가공
- 오늘 날짜를 기준으로 가장 최근 주문 일자를 뺀 날짜
- 주의할 점은 오늘 날짜를 현재 날짜로 해서는 안된다는 것
- 데이터가 10.12.1 ~ 11.12.9까지의 데이터이므로, 오늘 날짜는 11.12.9에서 하루를 더한 11.12.10으로 하자
- 11.12.10을 현재 날짜로 간주, 가장 최근의 주문일자를 뺀 데이터에서 days 일자 데이터만 추출하자
import datetime as dt
cust_df['Recency'] = dt.datetime(2011, 12, 10) - cust_df['Recency']
cust_df['Recency'] = cust_df['Recency'].apply(lambda x: x.days+1)
print('cust_df 로우와 컬럼 건수는', cust_df.shape)
cust_df.head()[Out]
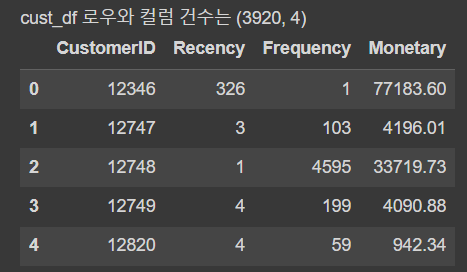
=> 이제 고객별로 RFM 분석에 필요한 컬럼을 모두 생성하였다.
RFM 기반 고객 세그먼테이션
생성된 고객 RFM 데이터셋의 특성을 개괄적으로 알아보고 고객세그먼테이션을 수행해보자.
- 앞서 말했듯이 개인 고객 뿐만 아니라, 소매업체의 대규모 주문을 포함하고 있기에, 군집화가 한쪽 군집에만 집중되는 현상이 발생할 것
- 먼저 데이터셋의 컬럼별 히스토그램을 확인하고, 왜곡적인 데이터 분포도에서 군집화를 수행할 때 어떤 현상이 발생하는지 알아보자
fig, (ax1, ax2, ax3) = plt.subplots(figsize=(12,4), nrows=1, ncols=3)
ax1.set_title('Recency Histogram')
ax1.hist(cust_df['Recency'])
ax2.set_title('Frequency Histogram')
ax2.hist(cust_df['Frequency'])
ax3.set_title('Monetary Histogram')
ax3.hist(cust_df['Monetary'])[Out]

=> 모두 왜곡된 데이터를 갖고 있다.
=> 특히, Frequency와 Monetary는 특정 범위에 값이 몰려있어 왜곡 정도가 매우 심함
df.describe()로 각 컬럼의 데이터 값 백분위로 대략적으로 어떻게 값이 분포되어있는지 확인해보자.
cust_df[['Recency', 'Frequency', 'Monetary']].describe()[Out]

=> Recency는 평균이 92.7이지만, 중위값(50%)인 51보다 크게 높다. 그리고 max값은 374로, 75%보다 훨씬 커서 왜곡 정도가 높음을 알 수 있음
=> Frequency와 Monetary의 경우는 왜곡 정도가 더 심해서 Frequency의 평균이 90.3인데, 75%인 99.25에 가깝다.
=> max 값 7847을 포함한 상위 몇 개의 큰 값으로 인한 것으로 보임
왜곡 정도가 매우 높은 데이터셋에 k-means 군집 적용시 중심의 개수를 증가시키더라도, 변별력없는 군집화가 수행되기 대문에, 먼저 StandardScaler으로 평균과 표준편차를 재조정한 뒤에 k-means를 수행해보자
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, silhouette_samples
X_features = cust_df[['Recency', 'Frequency', 'Monetary']].values
X_features_scaled = StandardScaler().fit_transform(X_features)
kmeans = KMeans(n_clusters=3, random_state=0)
labels = kmeans.fit_predict(X_features_scaled)
cust_df['cluster_label'] = labels
print('실루엣 스코어는 : {0:.3f}'.format(silhouette_score(X_features_scaled, labels)))[Out]
실루엣 스코어는 : 0.592군집을 3개로 구성할 경우, 전체 군집의 평균 실루엣 계수인 실루엣 스코어는 0.592로 안정적인 수치가 나왔다.
각 군집별 실루엣 계수 값은 어떤지 알아보자.
# 군집 평가에서 생성했던 함수 이용 (군집개수별로 군집화 구성을 시각화하는 함수)
visualize_silhouette([2,3,4,5], X_features_scaled)
visualize_kmeans_plot_multi([2,3,4,5], X_features_scaled)*함수 참고
visualize_silhouette
### 여러개의 클러스터링 갯수를 List로 입력 받아 각각의 실루엣 계수를 면적으로 시각화한 함수 작성
def visualize_silhouette(cluster_lists, X_features):
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import math
# 입력값으로 클러스터링 갯수들을 리스트로 받아서, 각 갯수별로 클러스터링을 적용하고 실루엣 개수를 구함
n_cols = len(cluster_lists)
# plt.subplots()으로 리스트에 기재된 클러스터링 수만큼의 sub figures를 가지는 axs 생성
fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)
# 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 실루엣 개수 시각화
for ind, n_cluster in enumerate(cluster_lists):
# KMeans 클러스터링 수행하고, 실루엣 스코어와 개별 데이터의 실루엣 값 계산.
clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
cluster_labels = clusterer.fit_predict(X_features)
sil_avg = silhouette_score(X_features, cluster_labels)
sil_values = silhouette_samples(X_features, cluster_labels)
y_lower = 10
axs[ind].set_title('Number of Cluster : '+ str(n_cluster)+'\n' \
'Silhouette Score :' + str(round(sil_avg,3)) )
axs[ind].set_xlabel("The silhouette coefficient values")
axs[ind].set_ylabel("Cluster label")
axs[ind].set_xlim([-0.1, 1])
axs[ind].set_ylim([0, len(X_features) + (n_cluster + 1) * 10])
axs[ind].set_yticks([]) # Clear the yaxis labels / ticks
axs[ind].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
# 클러스터링 갯수별로 fill_betweenx( )형태의 막대 그래프 표현.
for i in range(n_cluster):
ith_cluster_sil_values = sil_values[cluster_labels==i]
ith_cluster_sil_values.sort()
size_cluster_i = ith_cluster_sil_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_cluster)
axs[ind].fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_sil_values, \
facecolor=color, edgecolor=color, alpha=0.7)
axs[ind].text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
y_lower = y_upper + 10
axs[ind].axvline(x=sil_avg, color="red", linestyle="--")visualize_kmeans_plot_multi
### 여러개의 클러스터링 갯수를 List로 입력 받아 각각의 클러스터링 결과를 시각화
def visualize_kmeans_plot_multi(cluster_lists, X_features):
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
import pandas as pd
import numpy as np
# plt.subplots()으로 리스트에 기재된 클러스터링 만큼의 sub figures를 가지는 axs 생성
n_cols = len(cluster_lists)
fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)
# 입력 데이터의 FEATURE가 여러개일 경우 2차원 데이터 시각화가 어려우므로 PCA 변환하여 2차원 시각화
pca = PCA(n_components=2)
pca_transformed = pca.fit_transform(X_features)
dataframe = pd.DataFrame(pca_transformed, columns=['PCA1','PCA2'])
# 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 KMeans 클러스터링 수행하고 시각화
for ind, n_cluster in enumerate(cluster_lists):
# KMeans 클러스터링으로 클러스터링 결과를 dataframe에 저장.
clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)
cluster_labels = clusterer.fit_predict(pca_transformed)
dataframe['cluster']=cluster_labels
unique_labels = np.unique(clusterer.labels_)
markers=['o', 's', '^', 'x', '*']
# 클러스터링 결과값 별로 scatter plot 으로 시각화
for label in unique_labels:
label_df = dataframe[dataframe['cluster']==label]
if label == -1:
cluster_legend = 'Noise'
else :
cluster_legend = 'Cluster '+str(label)
axs[ind].scatter(x=label_df['PCA1'], y=label_df['PCA2'], s=70,\
edgecolor='k', marker=markers[label], label=cluster_legend)
axs[ind].set_title('Number of Cluster : '+ str(n_cluster))
axs[ind].legend(loc='upper right')
plt.show()[Out]

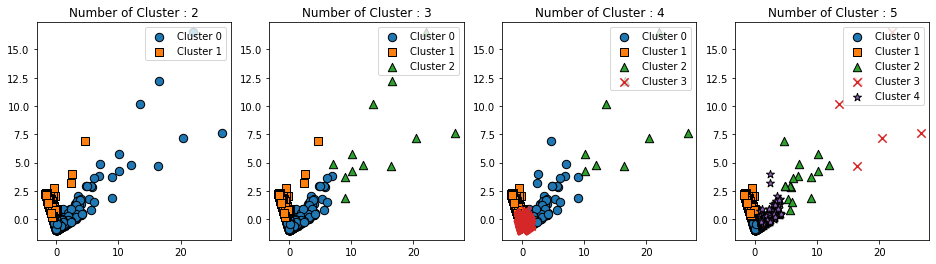
=> 군집이 2개일 경우, 0번 군집과 1전 군집이 너무 개괄적으로 군집화 됨
=> 군집이 3개 이상일 때부터는 데이터셋의 개수가 너무 작은 군집이 만들어짐, 이 군집에 속한 데이터 개수가 작을뿐더러, 실루엣 계수도 상대적으로 매우 작다. 또한, 군집 내부에서도 데이터가 광범위하게 퍼져있다.
=> 군집이 3개일 때는 0번 군집의 데이터 개수가 너무 적다.
=> 군집이 4개일 때는 2번,3번 군집이,
=> 5개일 때는 2,3,4번 군집에 속한 데이터셋의 개수가 너무 적고 광범위하게 퍼져있다.
=> 데이터 수가 적고, 광범위하게 퍼져있는 데이터는 왜곡된 데이터값인 소매점의 대량 주문 구매데이터이다.
- 왜곡된 데이터셋은 k-평균과 같은 거리 기반 군집화 알고리즘에서 지나치게 일반적인 군집화 결과를 도출하게 된다.
- 비지도학습 알고리즘 군집화의 기능적 의미는 "숨어 있는 새로운 집단을 발견하는 것"이다.
- 새로운 군집 내의 데이터 값을 분석하고 이해함으로써 집단에 새로운 의미를 부여할 수 있다.
- 이를 통해 전체 데이터를 다른 각도로 바라볼 수 있게 만들어줌!
데이터 셋의 왜곡 정도를 낮추기위해 자주 사용되는 방법은 데이터 값에 로그를 적용하는 '로그 변환'
로그 변환을 적용한 뒤 Kmeans를 수행해보자
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score, silhouette_samples
# Recency, Frequency, Monetary 컬럼에 np.log1p()로 log transformation
cust_df['Recency_log'] = np.log1p(cust_df['Recency'])
cust_df['Frequency_log'] = np.log1p(cust_df['Frequency'])
cust_df['Monetary_log'] = np.log1p(cust_df['Monetary'])
# Log Transfmroation 데이터에 StandardScaler 적용
X_features = cust_df[['Recency_log', 'Frequency_log', 'Monetary_log']].values
X_feauters_scaled = StandardScaler().fit_transform(X_features)
kmeans = KMeans(n_clusters=3, random_state=0)
labels = kmeans.fit_predict(X_features_scaled)
cust_df['cluster_label'] = labels
print('실루엣 스코어는 : {0:.3f}'.format(silhouette_score(X_features_scaled, labels)))[Out]
실루엣 스코어는 : 0.592로그변환한 데이터셋을 기반으로 실루엣 계수와 군집화 구성 시각화

=> 실루엣 계수는 로그 변환하기 전보다 떨어지긴 하지만,
=> 앞의 경우보다 더 균일하게 군집화가 구성되었음을 위 그림을 통해 알 수 있다.
=> 이처럼 왜곡된 데이터셋에 관해서는 로그 변환으로 데이터를 일차변환한 후에 군집화를 수행하면 더 나은 결과 도출
7-7. 정리
군집 분석
1. 군집화 기법은 나름의 장/단점을 갖고 있으며, 군집화하려는 데이터의 특성에 맞게 선택해야 한다.
2. k-means의 경우, 거리기반으로 군집 중심점을 이동시키면서 군집화를 수행
=> 데이터가 원데이터가 원형의 범위로 퍼져있을 때 효과적이다. 즉, 특정 데이터셋에만 잘 적용된다는 단점이 있다.
=> 복잡한 구조를 가진 데이터셋에 적용하기에는 한계가 있으며, 군집 개수를 최적화하기가 어렵다.
=> k-means는 군집이 잘되었는지 평가하기 위해 실루엣 계수 이용
3. 평균 이동(mean-shift)의 경우, k-means와 유사하지만, 거리 중심이 아니라, 데이터가 모여있는 밀도가 가장 높을 쪽으로 군집 중심점을 이동하면서 군집화 수행
=> 정형 데이터셋보다는 컴퓨터 비전 영역에서 뛰어난 역할 수행 (시간이 오래걸려 일반 분석에는 자주 사용되지X)
4. GMM(Gaussian Mixture Model)은 전체 데이터셋에서 서로 다른 정규분포 형태를 추출, 각각 군집화하는 방법
=> k-means보다 유연하게 다양한 구조를 가진 데이터셋에 적용 가능하나, 시간이 조금더 오래걸림
5. DBSCAN(Denstiy-Based Spatial Clustering of Applications with Noise)는 밀도 기반 군집화의 대표적인 알고리즘으로, 입실론 주변 영역 내에 포함되는 최소 데이터 개수 충족 여부로 데이터 포인트를 구분, 서로 연결하며 군집화를 구성하는 방식
=> 간단하고 직관적이지만, 데이터 분포가 기하학적으로 복잡한 데이터셋에도 효과적인 군집화가 가능




