| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 캐글 신용카드 사기 검출
- tableau
- 스태킹 앙상블
- splitlines
- 데이터 정합성
- 부트 스트래핑
- python
- 그로스 마케팅
- 분석 패널
- lightgbm
- 로그 변환
- 마케팅 보다는 취준 강연 같다(?)
- sql
- WITH ROLLUP
- WITH CUBE
- pmdarima
- 3기가 마지막이라니..!
- 그룹 연산
- 캐글 산탄데르 고객 만족 예측
- DENSE_RANK()
- ARIMA
- 컨브넷
- 그로스 해킹
- 데이터 핸들링
- 데이터 증식
- Growth hacking
- 리프 중심 트리 분할
- ImageDateGenerator
- XGBoost
- 인프런
- Today
- Total
LITTLE BY LITTLE
[10] 파이썬 머신러닝 완벽 가이드 - 5. 회귀 ( 비용 함수, 경사 하강법, LinearRegression() , RMSE = np.sqrt(-1*neg_mse_scores) ) 본문
[10] 파이썬 머신러닝 완벽 가이드 - 5. 회귀 ( 비용 함수, 경사 하강법, LinearRegression() , RMSE = np.sqrt(-1*neg_mse_scores) )
위나 2022. 9. 5. 23:065. 회귀
- 회귀 소개
- 단순 선형 회귀를 통한 회귀 이해
- 비용 최소화하기 - 경사 하강법 (Gradient Descent) 소개
- 사이킷런 Linear Regression을 이용한 보스턴 주택 가격 예측
- 다항 회귀와 과(대)적합/과소적합 이해
- 규제 선형 모델 - 릿지, 라쏘, 엘라스틱 넷
- 로지스틱 회귀
- 회귀 트리
- 회귀 실습 - 자전거 대여 수요 예측
- 회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
- 정리
- 차원 축소
- 차원 축소의 개요
- PCA (Principal Component Anlysis)
- LDA (Linear Discriminant Anlysis)
- SVD (Singular Value Decomposition)
- NMF (Non-Negative Matrix Factorization)
- 정리
- 군집화
- K-평균 알고리즘 이해
- 군집 평가
- 평균 이동 (Mean shift)
- GMM(Gaussian Mixture Model)
- DBSCAN
- 군집화 실습 - 고객 세그먼테이션
- 정리
- 텍스트 분석
- 텍스트 분석 이해
- 텍스트 사전 준비 작업(텍스트 전처리) - 텍스트 정규화
- Bag of Words - BOW
- 텍스트 분류 실습 - 20 뉴스그룹 분류
- 감성 분석
- 토픽 모델링 - 20 뉴스그룹
- 문서 군집화 소개와 실습 (Opinion Review 데이터셋)
- 문서 유사도
- 한글 텍스트 처리 - 네이버 영화 평점 감성 분석
- 텍스트 분석 실습 - 캐글 mercari Price Suggestion Challenge
- 정리
- 추천 시스템
- 추천 시스템의 개요와 배경
- 콘텐츠 기반 필터링 추천 시스템
- 최근접 이웃 협업 필터링
- 잠재요인 협업 필터링
- 콘텐츠 기반 필터링 실습 - TMDV 5000 영화 데이터셋
- 아이템 기반 최근접 이웃 협업 필터링 실습
- 행렬 분해를 이용한 잠재요인 협업 필터링 실습
- 파이썬 추천 시스템 패키지 - Surprise
- 정리
5-1. 회귀 소개
- 회귀분석은 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계적 기법
- "회귀"는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다.
- 지도 학습이 분류와 회귀 두 가지 유형으로 나뉘고, 두 기법의 가장 큰 차이는 분류는 예측값이 카테고리와 같은 이산형 클래스 값이고, 회귀는 연속형 숫자 값이라는 것이다.
- 선형회귀는 실제 값과 예측 값의 차이(오류의 제곱값)를 최소화하는 직선형 회귀선을 최적화하는 방식
- 선형 회귀는 규제 방법에 따라 별도의 유형으로 나뉨
- 규제는 일반적인 선형회귀의 과적합 문제를 해결하기 위해 회귀 계수에 페널티 값을 적용하는 것을 말함
- 일반 선형 회귀 : RSS(Residual Sum Of Squares)를 최소화, 규제 적용 X 모델
- 릿지 : 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델 (L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀계수 값을 더 작게 만드는 규제 모델)
- 라쏘 : 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식
- Elastic Net : L2, L1 규제를 함께 결합한 모델, 주로 피처가 많은 데이터셋에 적용, L1규제로 피처의 개수를 줄이고, L2 규제로 계수 값의 크기를 조정
- 로지스틱 회귀 : 회귀라는 이름이 붙어있으나, 분류에 사용되는 선형 모델. 일반적으로 이진 분류 뿐만 아니라, 희소 영역의 분류, 예를 들어 텍스트 분류와 같은 영역에서 뛰어난 예측 성능을 보임
- 규제는 일반적인 선형회귀의 과적합 문제를 해결하기 위해 회귀 계수에 페널티 값을 적용하는 것을 말함
- 선형 회귀는 규제 방법에 따라 별도의 유형으로 나뉨
5-2. 단순 선형 회귀를 통한 회귀 이해
- 최적의 회귀 모델을 만든다는 것은 전체 데이터의 잔차 합이 최소가 되는 모델을 만드는 것, 동시에 오류 값 합이 최소가 될 수 있는 최적의 회귀계수를 찾는다는 의미
- 오류 합은 +나 -가 될 수 있기에, 절댓값을 취해 더하거나(MSE), 오류 값의 제곱을 구해서 더함(RSS). 보통 미분등의 계산을 편하기 하기 위해서 RSS 방식으로 오류합을 구한다.
- 즉, RSS를 최소로하는 w0과 w1 회귀계수를 학습을 통해서 찾는 것이 머신러닝 기반 회귀의 핵심 사항
- RSS는 회귀식의 독립변수 X, 종속변수 Y가 중심 변수가 아니라, w변수(회귀 계수)가 중심변수임을 인지하기 (즉, 학습 데이터로 입력되는 독립변수와 종속변수는 RSS에서 모두 상수로 간주)
- 일반적으로 RSS는 학습 데이터의 건수로 나누어 정규화된 식으로 표현
- 회귀에서 이 RSS는 '비용'이며, w변수(회귀 계수)로 구성되는 RSS를 비용함수라 한다.
- 머신러닝 회귀 알고리즘은 데이터를 계속 학습하며, 이 비용함수가 반환하는 값(오류 값)을 지속해서 감소시키고, 최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것 (비용 함수 = 손실 함수)
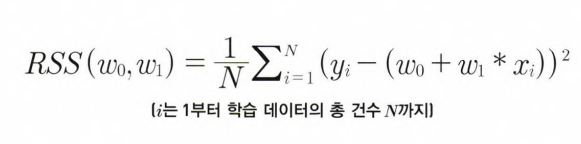
5-3. 비용 최소화하기 - 경사 하강법



- 비용 함수가 최소가 되는 w파라미터 구하기
- w 파라미터의 개수가 많을 시 고차원 방정식으로 도출하기 어려움
- 경사 하강법은 이러한 고차원 방정식에 대한 문제를 해결해주면서 비용함수 RSS를 최소화하는 방법을 직관적으로 제공
- 경사 하강법은, 점진적으로 반복적인 계산을 통해 w파라미터 값을 업데이트하면서 오류 값이 최소가되는 w파라미터를 구하는 방식
- 반복적으로 비용 함수의 반환값, 즉, 예측 값과 실제 값의 차이가 작아지는 방향성을 가지고 w파라미터를 지속해서 보정해 나간다.
- 최소 오류 값이 100이었다면, 두 번째 오류 값은 100보다 작은 90, 세 번째는 80과 같은 방식으로 지속해서 오류를 감소시키는 방향으로 w값을 계속 업데이트해나간다. 더 이상 작아지지 않을 때 최소 비용으로 판단, 그 때의 w값을 최적 파라미터로 반환
- 경사 하강법의 일반적인 프로세스
- step 1. w1, w0을 임의로 설정하고, 첫 비용 함수의 값을 계산
- step 2 : w1과 w0을 각각 R(W)를 편미분한 값으로 (위 그림 참고) 업데이트 한 후 다시 비용 함수 계산값을 계산
- step 3 : 비용 함수 값이 감소했으면, 다시 step2를 반복. 더 이상 비용 함수의 값이 감소하지 않으면 그 떄의 w0, w1을 구하고 반복을 중지
경사 하강법 코드로 구현
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y = 4x + 6을 근사(w1=4, w0=6). 임의의 값은 노이즈를 위해 만듦
X = 2 * np.random.rand(100,1)
y = 6 + 4 * X+np.random.randn(100,1)
# X, y 데이터 셋 산점도로 시각화
plt.scatter(X,y)참고 : 난수 생성(▼)
np.random.randint (시작,n-1) 균일 분포의 정수 난수 1개 생성
np.random.rand (m,n) 0부터 1사이의 균일 분포에서 난수를 matrix array (m,n)생성
np.random.randn(m,n) 가우시안 표준 정규 분포에서 난수 matrix array (m,n) 생성

비용 함수를 정의해보자.

def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
경사 하강법을 gradient_descent()라는 함수를 생성해 구현해보자.
- w1과 w0을 모두 0으로 초기화한 뒤, iters 개수만큼 반복하면서 w1과 w0을 업데이트 한다.
- gradient_descent()는 위에서 무작위로 생성한 X와 y를 입력받는데, X와 y 모두 넘파이 ndarray이다.
- get_weight_updates()
- get_weight_updates 함수에서, 입력 배열 X값에 대한 예측 배열 y_pred는 np.dot(X, w1.T) + w0으로 구한다.
- 또한 get_weight_updates()는 w1_update와 w0_update로 예측 오류를 넘파이의 dot 행렬 연산으로 계산한 뒤 이를 반환한다.
# w1과 w0을 업데이트 할 w1_update, w0_update를 반환
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
# 먼저 w1_update, w0_update를 각각 w1,w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
# 예측 배열 계산하고 예측과 실제 값 차이 계산
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
# w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트 할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T,diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T,diff))
return w1_update, w0_update생성한 함수 get_weight_updates()를 경사하강 방식으로 반복적으로 수행하여 w1과 w0을 업데이트 하는 함수인 gradient_descent_steps() 생성
# 입력인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0 업데이트 적용함
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters만큼 반복적으로 get_weight_updates() 호출해 w1, w0 업데이트 수행
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0생성한 함수 greadient_descent_steps 호출해 w1과 w0 구하기 (get_cost() 함수 생성)
def get_costs(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0],w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y,y_pred)))[Out]
w1:4.022 w0:6.162
Gradient Descent Total Cost:0.9935=> 실제 선형 식인 y=4X + 6과 유사하게, w1은 4.022, w0는 6.162가 도출되었다. 예측 오류비용은 0.9935
plt.scatter(X,y)
plt.plot(X,y_pred)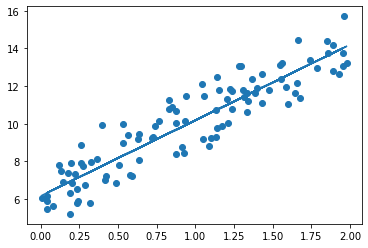
- 경사 하강법은 시간이 오래걸린다는 단점이 있기에, 대부분 확률적 경사 하강법 (Stochastic Gradient Descent)를 이용한다.
- 따라서 대용량의 데이터의 경우, 대부분 확률적 경사 하강법이나 미니 배치 확률적 경사 하강법을 이용해 최적 비용함수를 도출한다.
(미니 배치) 확률적 경사 하강법을 gradient_descent_steps()함수로 구현해보자
=> 경사 하강법과의 차이점은 전체 X,y 데이터에서 랜덤하게 batch_size만큼 데이터를 추출해 이를 기반으로 w1_update, w0_update를 계산하는 부분에만 차이가 있다.
(▼)이 부분

# (미니배치) 확률적 경사 하강법 구현
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index = 0
for ind in range(iters):
np.random.seed(ind)
# 전체 X, y 데이터에서 랜덤하게 batch_size 만큼 데이터를 추출해 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1,w0,sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
w1, w0 = stochastic_gradient_descent_steps(X,y,iters=1000)
print("w1:", round(w1[0,0], 3),"w0:", round(w0[0,0],3))
y_pred = w1[0,0]*X+w0
print('Stochastic Gradient Descent Total Cost : {0:.4f}'.format(get_cost(y,y_pred)))[Out]
w1: 4.028 w0: 6.156
Stochastic Gradient Descent Total Cost : 0.9937=> 예측 성능상 큰 차이는 없다.
피처가 여러 개인 경우 회귀 계수를 도출하는 경우에 대해 알아보자. 1개인 경우를 확장해 유사하게 도출할 수 있다.
앞서 예측 행렬 y_pred는 개별적으로 X의 개별 원소와 w1의 값을 곱하지 않고,

를 이용해 계산하였다. 마찬가지로, 데이터 개수가 N이고, 피처 M개의 입력 행렬을 Xmat, 회귀 계수 w1,w2,...w100을 w배열로 표기하면 예측 행렬 y햇은 위 식에서 X => Xmat , w1.T => W^t 로 바꾸어 구할 수 있다.
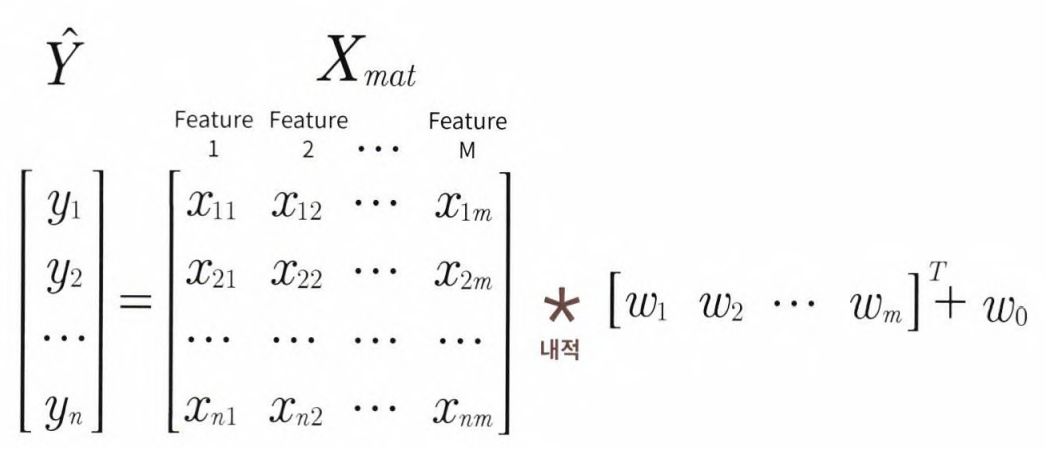
w0를 weight의 배열인 w안에 포함시키기 위해서 xmat의 맨처음 열에 모든 데이터 값이 1인 피처 feat 0을 추가하면, 회귀 예측값 y햇은 다음과 같다.

5-4. 사이킷런 Linear Regressions을 이용한 보스턴 주택 가격 예측
LinearRegressioin 클래스 - Ordinary Least Squares
class sklearn.linear_model.LinearRegression ( fit_intercept = True, normalize=False, copy_X=True, n_jobs=1)
- fit_intercept : boolean 값으로, 디폴트는 True, intercept(절편) 값을 계산할 것인지 말지 지정함. False로 지정시, intercept가 사용되지 않고, 0으로 지정된다.
- normalize : boolean 값으로, 디폴트는 Flase. fit_intercept가 False인 경우, 이 파라미터는 무시됨, True일시 회귀 수행 이전에 입력 데이터셋 정규화
- 속성 coef_ : fit() 메소드 수행시 회귀 계수가 배열 형태로 저장하는 속성, shape는 (target 값 개수, 피처 개수)
- 속성 intercept_ : intercept 값
- Ordinary Least Sqaures 기반의 회귀계수 계산은 입력 피처의 독립성에 영향을 많이 받는다. 피처간의 상관관계가 매우 높은 경우, 분산이 매우 커져서 오류에 매우 민감해진다. => 다중 공선성
- 일반적으로 상관관계가 높은 피처가 많은 경우, (1)독립적인 중요한 피처만 남기고 제거하거나, (2)규제를 적용한다.
- 또한 매우 많은 피처가 다중 공선성 문제를 가지고 있다면, (3)PCA를 통해 차원 축소를 수행하는 것도 고려해볼 수 있다.
회귀 평가 지표
- MAE : metrics.mean_absolute_error ( neg_mean_absolute_error )
- MSE : metrics.mean_squared_error ( neg_mean_squared_error )
- R^2 : metrics.r2_score ( r2 )
- 괄호 안은 cross_val_score나 GridSerachCV에서 평가시 사용되는 scoring 파라미터의 적용 값
- neg_라는 접두어는 negative의 약자인데, mae는 절댓값의 합이기 때문에 음수가 될 수 없다. 의미 해석시 주의

Linear Regression을 이용해 보스턴 주택 가격 회귀 구현

데이터 셋 로드하고 df로 변환하기
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from sklearn.datasets import load_boston
%matplotlib inline
boston = load_boston()
bostonDF = pd.DataFrame(boston.data, columns = boston.feature_names)
# boston 타겟 배열은 "주택 가격", 이를 price 컬럼으로 df에 추가하기
bostonDF['PRICE'] = boston.target
print('Boston 데이터셋 크기:', bostonDF.shape)
bostonDF.head()[Out]
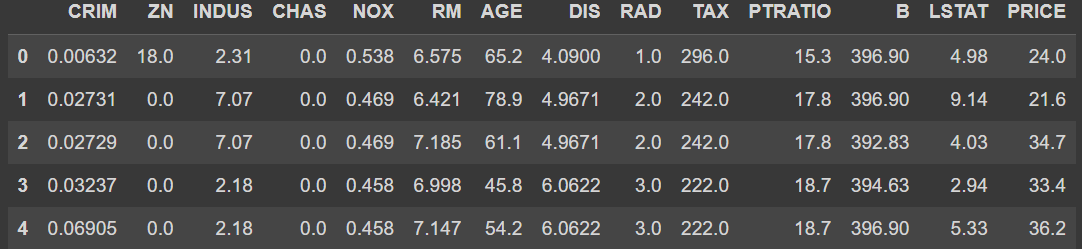
=> 데이터 셋 피처의 Null 값은 없다.
=> 모두 float 형
각 칼럼이 회귀 결과에 미치는 영향이 어느정도인지 확인해보자. (Seaborn 이용)
# 2개의 행과 4개의 열을 가진 subplots 이용, axs는 4x2개의 ax를 가짐
fig, axs = plt.subplots(figsize=(16,8), ncols=4, nrows=2)
lm_features = ['RM', 'ZN', 'INDUS', 'NOX', 'AGE', 'PTRATIO', 'LSTAT', 'RAD']
for i, feature in enumerate(lm_features):
row = int(i/4)
col = i%4
# seaborn의 regplot을 이용해 산점도와 선형 회귀 직선 함께 표현
sns.regplot(x=feature, y='PRICE', data=bostonDF, ax=axs[row][col])* enumerate
enumerate() 함수는 인자로 넘어온 목록을 기준으로 인덱스와 원소를 차례대로 접근하게 해주는 반복자(iterator) 객체를 반환해주는 함수
[Out]

=> 다른 칼럼보다 RM(1번째,양의 선형성)과 LSTAT(7번째,음의 선형성)의 PRICE 영향도가 두드러지게 나타난다
이제 LinearRegression 클래스를 이용해 회귀 모델을 만들어보자. (세트 분리 후 학습,예측 수행, mse와 R2 score측정)
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'], axis=1, inplace=False)
# 분리
X_train, X_test, y_train, y_test = train_test_split(X_data, y_target, test_size=0.3,random_state=156)
# 선형회귀 OLS[최소자승법]로 학습/예측/평가 수행
lr = LinearRegression()
lr.fit(X_train, y_train)
y_preds = lr.predict(X_test)
mse = mean_squared_error(y_test, y_preds)
rmse = np.sqrt(mse)
print('MSE : {0:.3f}, RMSE : {1:.3f}'.format(mse, rmse))
print('Variance Score : {0:.3f}'.format(r2_score(y_test, y_preds)))LinearRegression으로 생성한 주택 가격 모델의 intercept(절편)과 coefficients(회귀 계수) 값을 확인해 보자.
print('절편 값:' , lr.intercept_)
print('회귀 계수값:', np.round(lr.coef_))[Out]
절편 값: 40.99559517216477
회귀 계수값: [ -0. 0. 0. 3. -20. 3. 0. -2. 0. -0. -1. 0. -1.]coef_ 속성은 회귀 계수 값만 갖고 있음
=> 회귀 계수를 피처별 회귀 계수 값으로 매핑하고, 높은 값 순으로 출력해보자.
# 회귀 계수를 큰 값 순으로 정렬하기 위해 Series로 생성, 인덱스 칼럼명에 유의
coeff = pd.Series(data = np.round(lr.coef_, 1), index=X_data.columns)
coeff.sort_values(ascending=False)[Out]
RM 3.4
CHAS 3.0
RAD 0.4
ZN 0.1
INDUS 0.0
AGE 0.0
TAX -0.0
B 0.0
CRIM -0.1
LSTAT -0.6
PTRATIO -0.9
DIS -1.7
NOX -19.8
dtype: float64=> RM이 양의 값으로 회귀 계수가 가장 크며, NOX 피처의 회귀 계수 - 값이 너무 커보인다. 최적화를 수행하면서 피처의 회귀 계수의 변화를 살펴볼 예정
이번에는 5개의 폴드 세트에서 cross_val_score()를 이용해 교차 검증으로 MSE와 RMSE를 측정해보자.
- 사이킷런의 cross_val_score()은 RMSE를 제공하지 않기 때문에, MSE 수치를 RMSE로 변환해야한다.
- 앞서 보았듯이 cross_val_score()의 인자로 scoring='neg_mean_squred_error'지정시 반환되는 수치 값은 음수이다.
- 회귀는 MSE값이 낮을 수록 좋은 회귀 모델이기에, -1을 곱해서 반환하도록 하자.
- 이렇게 다시 변환된 MSE값에 넘파이의 sqrt()함수로 RMSE 구하기
from sklearn.model_selection import cross_val_score
y_target = bostonDF['PRICE']
X_data = bostonDF.drop(['PRICE'],axis=1, inplace=False)
lr = LinearRegression()
# cross_val_score()로 5 폴드 세트로 MSE를 구한 뒤, 이를 기반으로 다시 RMSE 구함
neg_mse_scores = cross_val_score(lr, X_data, y_target, scoring="neg_mean_squared_error", cv=5)
rmse_scores = np.sqrt(-1*neg_mse_scores)
avg_rmse = np.mean(rmse_scores)
# cross_val_score(scoring="neg_mean_squred_error")로 반환된 값은 모두 음수
print( '5 folds의 개별 Negative MSE scores:', np.round(neg_mse_scores,2))
print('5 folds의 개별 RSME scores:', np.round(rmse_scores, 2))
print('5 folds의 평균 RMSE : {0:.3f}'.format(avg_rmse))[Out]
5 folds의 개별 Negative MSE scores: [-12.46 -26.05 -33.07 -80.76 -33.31]
5 folds의 개별 RSME scores: [3.53 5.1 5.75 8.99 5.77]
5 folds의 평균 RMSE : 5.829=> 5개 폴드 세트에 대해서 교차 검증을 수행한 결과, 평균 rmse는 약 5.829가 나왔다.




