| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- pmdarima
- 스태킹 앙상블
- tableau
- 데이터 증식
- 캐글 신용카드 사기 검출
- 컨브넷
- python
- sql
- 데이터 핸들링
- 리프 중심 트리 분할
- 부트 스트래핑
- XGBoost
- ARIMA
- 3기가 마지막이라니..!
- WITH ROLLUP
- 그룹 연산
- WITH CUBE
- 마케팅 보다는 취준 강연 같다(?)
- DENSE_RANK()
- 분석 패널
- 인프런
- Growth hacking
- 로그 변환
- 캐글 산탄데르 고객 만족 예측
- ImageDateGenerator
- 데이터 정합성
- 그로스 해킹
- lightgbm
- 그로스 마케팅
- splitlines
- Today
- Total
LITTLE BY LITTLE
[11] 파이썬 머신러닝 완벽 가이드 - 7. 군집화 : K-평균 알고리즘 이해 (KMeans(), kmeans.label_, plt.scatter로 군집 시각화, make_blobs(), cluster_std ..) 본문
[11] 파이썬 머신러닝 완벽 가이드 - 7. 군집화 : K-평균 알고리즘 이해 (KMeans(), kmeans.label_, plt.scatter로 군집 시각화, make_blobs(), cluster_std ..)
위나 2022. 9. 11. 12:077. 군집화
- K-평균 알고리즘 이해
- 군집 평가
- 평균 이동 (Mean shift)
- GMM(Gaussian Mixture Model)
- DBSCAN
- 군집화 실습 - 고객 세그먼테이션
- 정리
- 회귀
- 다항 회귀와 과(대)적합/과소적합 이해
- 규제 선형 모델 - 릿지, 라쏘, 엘라스틱 넷
- 로지스틱 회귀
- 회귀 트리
- 회귀 실습 - 자전거 대여 수요 예측
- 회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
- 정리
- 차원 축소
- 차원 축소의 개요
- PCA (Principal Component Anlysis)
- LDA (Linear Discriminant Anlysis)
- SVD (Singular Value Decomposition)
- NMF (Non-Negative Matrix Factorization)
- 정리
-
- 텍스트 분석
- 텍스트 분석 이해
- 텍스트 사전 준비 작업(텍스트 전처리) - 텍스트 정규화
- Bag of Words - BOW
- 텍스트 분류 실습 - 20 뉴스그룹 분류
- 감성 분석
- 토픽 모델링 - 20 뉴스그룹
- 문서 군집화 소개와 실습 (Opinion Review 데이터셋)
- 문서 유사도
- 한글 텍스트 처리 - 네이버 영화 평점 감성 분석
- 텍스트 분석 실습 - 캐글 mercari Price Suggestion Challenge
- 정리
- 추천 시스템
- 추천 시스템의 개요와 배경
- 콘텐츠 기반 필터링 추천 시스템
- 최근접 이웃 협업 필터링
- 잠재요인 협업 필터링
- 콘텐츠 기반 필터링 실습 - TMDV 5000 영화 데이터셋
- 아이템 기반 최근접 이웃 협업 필터링 실습
- 행렬 분해를 이용한 잠재요인 협업 필터링 실습
- 파이썬 추천 시스템 패키지 - Surprise
- 정리
7-1. K-평균 알고리즘 이해

- K-평균은 군집화(Clustering)에서 일반적으로 사용되는 알고리즘으로, 군집 중심점(centroid)이라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법
- (+) 일반적인 군집화에서 가장 많이 활용된다, 알고리즘이 쉽고 간결하다.
- (-) 거리 기반 알고리즘으로 속성의 개수가 많을 경우 군집화 정확도가 떨어진다.( PCA로 차원축소 적용 필요 )
- (-) 반복 횟수가 많을 경우 수행 시간이 매우 느려짐, 몇 개의 군집을 선택해야할지 가이드하기가 어려움
- 사이킷런 Kmeans 클래스 소개
- class sklearn.cluster.KMeans(n_cluster=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto')
- 중요 파라미터
- n_clusters : 군집화할 개수, 즉 군집 중심점의 개수
- init : 초기에 군집 중심점의 좌표를 설정할 방식을 말하며, 보통은 임의로 중심을 설정하지 않고, 일반적으로 k-means++방식으로 최초 설정한다.
- max_iter는 최대 반복횟수, 횟수 이전에 모든 데이터의 중심점 이동이 없으면 종료한다.
- 사이킷런의 비지도학습과 마찬가지로 fit(데이터 세트) 또는 fit_transform(데이터 세트) 메소드를 이용해 수행하면 된다. 수행된 KMeans 객체는 군집화 수행이 완료되어 군집화와 관련된 주요 속성을 알 수 있다.
- labels_ : 각 데이터 포인트가 속한 군집 중심점 레이블
- cluster_centers_ : 각 군집 중심점 좌표(Shape는 [군집 개수, 피처 개수]). 이를 이용하면 군집 중심점 좌표가 어디인지 시각화 가능
- K-평균을 이용한 붓꽃 데이터 셋 군집화
from sklearn.preprocessing import scale
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inlineiris = load_iris()
# 데이터 핸들링 하기 위해 Dataframe으로 변환
irisDF = pd.DataFrame(data=iris.data, columns=['sepal_length', 'sepal_width', 'petal_length','petal_width'])
irisDF.head(3)붓꽃 데이터 셋을 3개 그룹으로 군집화 해보자.
- n_clusters = 3
- 초기 중심 설정 방식은 디폴트 값인 k-means++으로
- 최대 반복 횟수 역시 디폴트 값인 max_iter=300으로 설정하고
- fit() 수행
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=0)
kmeans.fit(irisDF)
print(kmeans.labels_)[Out]
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 2 2 2 0 2 2 2 2
2 2 0 0 2 2 2 2 0 2 0 2 0 2 2 0 0 2 2 2 2 2 0 2 2 2 2 0 2 2 2 0 2 2 2 0 2
2 0]=> labels_의 값이 0,1,2로 되어있으며, 이는 각 레코드가 첫 번째 군집, 두 번째 군집, 세 번째 군집에 속함을 의미함
실제 붓꽃 품종 분류 값과 얼마나 차이가 나는지 보아 군집화가 효과적으로 되었는지 확인해보자
- 붓꽃 데이터 셋의 target 값을 'target' 칼럼으로
- 앞서 구한 labels_ 값을 'cluster' 칼럼으로 지정
- irisDF DataFrame에 추가한 뒤에 group by 연산을 실제 분류값인 target과 군집화 분류 값인 cluster 레벨로 적용해서 target과 cluster값 개수를 비교
irisDF['target'] = iris.target
irisDF['cluster'] = kmeans.labels_
iris_result = irisDF.groupby(['target', 'cluster'])['sepal_length'].count()
print(iris_result)[Out]
target cluster
0 1 50
1 0 48
2 2
2 0 14
2 36
Name: sepal_length, dtype: int64=> 분류 타깃이 0값인 데이터는 1번 군집으로 잘 그루핑되었다.
=> Target 1 값 데이터는 2개만 2번 군집으로 그루핑되었고, 나머지 48개는 모두 0번 군집으로 그루핑되었다.
=> 하지만 Target 2 값의 데이터는 0번 군집에 14개, 2번 군집에 36개로 분산돼 그루핑되었다.
이번에는 붓꽃 데이터 셋의 군집화를 시각화해보자.
- 2차원 평면상에서 개별데이터의 군집화 표현
- 속성이 4개이므로, 2차원 평면에 적합하지 않음
- 따라서 PCA를 이용해 4개의 속성을 2개로 차원 축소한 뒤에 X,Y좌표로 개별 데이터를 표현해보자
# 군집 값이 0,1,2인 경우마다 별도의 인덱스로 추출
marker0_ind = irisDF[irisDF['cluster']==0].index
marker1_ind = irisDF[irisDF['cluster']==1].index
marker2_ind = irisDF[irisDF['cluster']==2].index
# 군집 값이 0,1,2에 해당하는 인덱스로 각 군집 레벨의 pca_x, pca_y 값 추출, o, s, ^로 마커 표시
plt.scatter(x=irisDF.loc[marker0_ind, 'pca_x'], y=irisDF.loc[marker0_ind, 'pca_y'], marker='o')
plt.scatter(x=irisDF.loc[marker1_ind, 'pca_x'], y=irisDF.loc[marker1_ind, 'pca_y'], marker='s')
plt.scatter(x=irisDF.loc[marker2_ind, 'pca_x'], y=irisDF.loc[marker2_ind, 'pca_y'], marker='^')
plt.xlabel('PCA1')
plt.ylabel('PCA2')
plt.title('3 Clusters Visualization by 2 PCA Components')
plt.show()[Out]
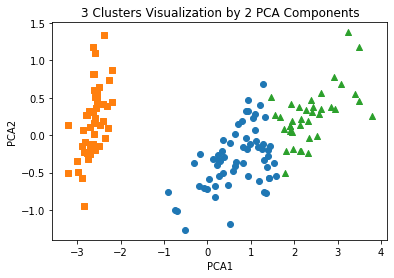
=> cluster1을 나타내는 네모(주황색)는 명확히 다른 군집과 분리가 잘 되어있다.
=> cluster0을 나타내는 동그라미(파란색)와 clsuter2를 나타내는 세모(초록색)는 상당 수준 분리되어있지만, 네모만큼 명확하게 분리되어있지는 않음을 알 수 있다.
=> cluster0과 cluster1의 경우, 속성의 위치 자체가 명확히 분리되기 어려운 부분이 존재한다.
군집화 알고리즘 테스트를 위한 데이터 생성
- 군집화 알고리즘을 테스트해보기 위한 간단한 데이터 생성기
- make_blobs() : 개별 군집의 중심점과 표준 편차 제어 기능 포함
- n_samples : 생성할 총 데이터 개수, 디폴트는 100개
- n_features : 피처 개수, 시각화를 목표로 할 경우 2개로 설정, 1번째는 x좌표, 2번쨰는 y좌표에 표현
- centers : int 값, 예를 들어 3으로 설정하면 군집의 개수를 나타낸다. ndarray형태로 표현할 경우 개별 군집 중심점의 좌표를 의미함
- cluster_std : 생성될 군집 데이터의 표준편차를 의미, 군집별로 서로 다른 표준편차를 가진 데이터셋을 만들 때 사용
- 만일 float값 0.8과 같은 형태로 지정하면 군집 내에서 데이터가 표준편차 0.8을 가진 값으로 만들어진다. [0.8, 1.2, 0.6]과 같은 형태로 표현되면 3개의 군집에서 첫번째 군집 내 데이터의 표준편차는 0.8, 두번째는 1.2, 세번째는 0.6으로 만듦
- make_classification() : 노이즈를 포함한 데이터를 만드는데 유용하게 사용할 수 있다.
- 둘다 분류용도로도 테스트 데이터 생성 가능
- 이외에 make_circle(), make_moon()는 api중심 기반의 군집화로 해결하기 어려운 데이터셋을 만드는데 사용됨
- make_blobs() : 개별 군집의 중심점과 표준 편차 제어 기능 포함
# make_blos()로 군집화용 데이터 생성
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
%matplotlib inlineX, y = make_blobs(n_samples=200, n_features=2, centers=3, cluster_std=0.8, random_state=0)
print(X.shape, y.shape)
# y target 값의 분포를 확인
unique, counts = np.unique(y, return_counts=True)
print(unique, counts)[Out]
(200, 2) (200,)
[0 1 2] [67 67 66]=> 200개의 레코드와 2개의 피처
=> 군집 데이터세트인 y의 shape은 (200,)
=> 3개의 cluster 값은 [0,1,2]이며, 각각 67,67,66개로 균일하게 구성되어있다.
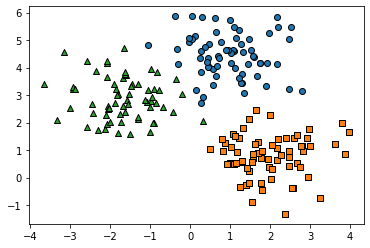
데이터 가공을위해 DataFrame으로 변환하고, make_blobs()로 만든 피처 데이터셋이 어떠한 군집화 분포를 가지고 만들어졌는지 확인해보자.
target_list = np.unique(y)
# 각 타깃별 산점도의 마커 값
markers = ['o', 's', '^', 'P', 'D', 'H', 'x']
# 3개의 군집 영역으로 구분한 데이터셋을 생성했으므로 target_list는 [0,1,2]
# target==0, target==1, target==2로 scatter plot을 marker별로 생성
for target in target_list:
target_cluster = clusterDF[clusterDF['target']==target]
plt.scatter(x=target_cluster['ftr1'],y=target_cluster['ftr2'],edgecolor='k',marker=markers[target])
plt.show()[Out]
이번에는 만들어진 데이터셋에 KMeans 군집화를 수행한 뒤에, 군집별로 시각화해보자.
- 먼저 KMeans 객체에 fit_predict(X)를 수행해 make_blobs()의 피처 데이터셋인 X데이터를 군집화한다.
- 이를 앞서 구한 clusterDF DataFrame의 'kmeans_label'칼럼으로 저장
- KMenas 객체의 cluster_centers_ 속성은 개별 군집의 중심 위치 좌표를 나타내기 위해 사용
# KMeans 객체를 이용해 X데이터를 K-Means 클러스터링 수행
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=200, random_state=0)
cluster_labels = kmeans.fit_predict(X)
clusterDF['kmeans_label'] = cluster_labels
# cluster_centers_는 개별 클러스터의 중심 위치 좌표 시각화를 위해 추출
centers = kmeans.cluster_centers_
unique_labels = np.unique(cluster_labels)
markers = ['o','s','^','P','D','H','x']
# 군집된 label 유형벼로 iteration 하면서 marker별로 scatter plot 수행
for label in unique_labels:
label_cluster = clusterDF[clusterDF['kmeans_label']==label]
center_x_y = centers[label]
plt.scatter(x=label_cluster['ftr1'], y=label_cluster['ftr2'], edgecolor='k',
marker=markers[label])
# 군집별 중심 위치 좌표 시각화
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=200, color='white',
alpha=0.9, edgecolor='k', marker=markers[label])
plt.scatter(x=center_x_y[0], y=center_x_y[1], s=70, color='k', edgecolor='k',
marker='$%d$' % label)
plt.show()[Out]
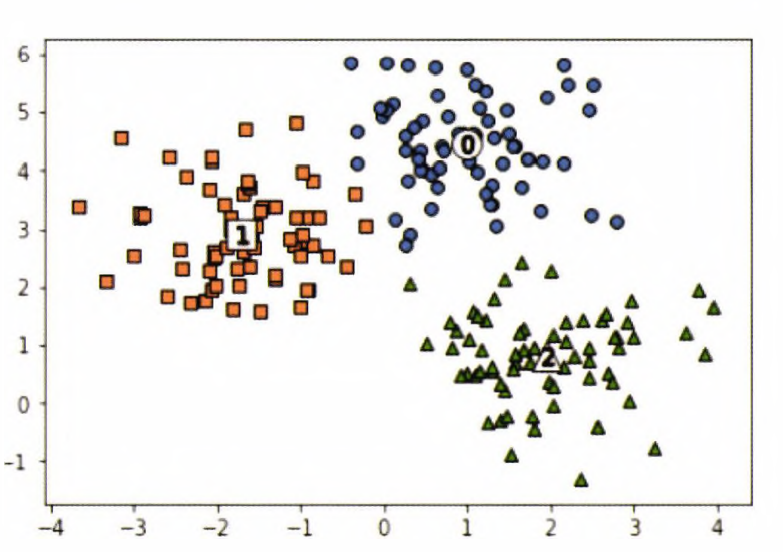
=> make_blobs()의 타깃과 kmeans_label은 군집 번호를 의미하므로, 서로 다른 값으로 매핑될 수 있다. 그래서 산점도의 마커가 서로 다를 수 있다.
print(clusterDF.groupby('target')['kmeans_label'].value_counts())[Out]
target kmeans_label
0 0 66
1 1
1 2 67
2 1 65
2 1
Name: kmeans_label, dtype: int64=> Target0이 cluster label이 0으로, Target1이 cluster label 2로, Target2가 cluster labl1으로 거의 대부분 잘 매핑됨
make_blobs()는 cluster_std 파라미터로 데이터의 분포도를 조절한다.

=> cluster_std가 0.4, 0.8, 1.2, 1.6일때의 데이터를 시각화 한 것
=> cluster_std가 작을수록 군집 중심에 데이터가 모여있고, 클수록 데이터가 퍼져있음을 알 수 있다.




