| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 캐글 신용카드 사기 검출
- splitlines
- 그로스 마케팅
- 스태킹 앙상블
- pmdarima
- sql
- 분석 패널
- 데이터 정합성
- tableau
- XGBoost
- lightgbm
- 인프런
- ImageDateGenerator
- 그룹 연산
- 마케팅 보다는 취준 강연 같다(?)
- python
- 리프 중심 트리 분할
- 로그 변환
- 컨브넷
- DENSE_RANK()
- 데이터 증식
- WITH ROLLUP
- 부트 스트래핑
- 데이터 핸들링
- 캐글 산탄데르 고객 만족 예측
- WITH CUBE
- Growth hacking
- ARIMA
- 그로스 해킹
- 3기가 마지막이라니..!
- Today
- Total
LITTLE BY LITTLE
[9] 파이썬 머신러닝 완벽 가이드 - 4. 분류(XGBoost&LightGBM 캐글 실습,로그 변환&이상치 제거&SMOTE 캐글 실습, 스태킹 앙상블) 본문
[9] 파이썬 머신러닝 완벽 가이드 - 4. 분류(XGBoost&LightGBM 캐글 실습,로그 변환&이상치 제거&SMOTE 캐글 실습, 스태킹 앙상블)
위나 2022. 8. 22. 11:174. 분류
분류의 개요결정 트리앙상블 학습랜덤 포레스트GBM(Gradient Boosting Machine)XGBoost(eXtra Gradient Boost)LightGBM- 분류 실습 - 캐글 산탄데르 고객 만족 예측
- 분류 실습 - 캐글 신용카드 사기 검출
- 스태킹 앙상블
- 정리
- 회귀
- 회귀 소개
- 단순 선형 회귀를 통한 회귀 이해
- 비용 최소화하기 - 경사 하강법 (Gradient Descent) 소개
- 사이킷런 Linear Regression을 이용한 보스턴 주택 가격 예측
- 다항 회귀와 과(대)적합/과소적합 이해
- 규제 선형 모델 - 릿지, 라쏘, 엘라스틱 넷
- 로지스틱 회귀
- 회귀 트리
- 회귀 실습 - 자전거 대여 수요 예측
- 회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
- 정리
- 차원 축소
- 차원 축소의 개요
- PCA (Principal Component Anlysis)
- LDA (Linear Discriminant Anlysis)
- SVD (Singular Value Decomposition)
- NMF (Non-Negative Matrix Factorization)
- 정리
- 군집화
- K-평균 알고리즘 이해
- 군집 평가
- 평균 이동 (Mean shift)
- GMM(Gaussian Mixture Model)
- DBSCAN
- 군집화 실습 - 고객 세그먼테이션
- 정리
- 텍스트 분석
- 텍스트 분석 이해
- 텍스트 사전 준비 작업(텍스트 전처리) - 텍스트 정규화
- Bag of Words - BOW
- 텍스트 분류 실습 - 20 뉴스그룹 분류
- 감성 분석
- 토픽 모델링 - 20 뉴스그룹
- 문서 군집화 소개와 실습 (Opinion Review 데이터셋)
- 문서 유사도
- 한글 텍스트 처리 - 네이버 영화 평점 감성 분석
- 텍스트 분석 실습 - 캐글 mercari Price Suggestion Challenge
- 정리
- 추천 시스템
- 추천 시스템의 개요와 배경
- 콘텐츠 기반 필터링 추천 시스템
- 최근접 이웃 협업 필터링
- 잠재요인 협업 필터링
- 콘텐츠 기반 필터링 실습 - TMDV 5000 영화 데이터셋
- 아이템 기반 최근접 이웃 협업 필터링 실습
- 행렬 분해를 이용한 잠재요인 협업 필터링 실습
- 파이썬 추천 시스템 패키지 - Surprise
- 정리
4-8. 분류 실습 - 캐글 산탄데르 고객 만족 예측
- 캐글의 산탄데르 고객 만족 데이터셋에 대해 고객 만족여부를 XGBoost와 LightGBM으로 예측해보자.
- 370개의 피처로 주어진 데이터셋 기반 고객 만족 여부 예측, 피처 이름은 익명처리되어 속성은 알 수 없음
- 클래스 레이블 명은 Target, 이 값이 1이면 불만을 가진 고객, 0이면 만족한 고객
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
cust_df = pd.read_csv("/content/train_santander.csv",encoding='latin-1')
print('dataset shape:', cust_df.shape)
cust_df.head(3)[Out]

# 피처의 타입과 Null 값 알아보기
cust_df.info()[Out]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 76020 entries, 0 to 76019
Columns: 371 entries, ID to TARGET
dtypes: float64(111), int64(260)
memory usage: 215.2 MBprint(cust_df['TARGET'].value_counts())
unsatisfied_cnt = cust_df[cust_df['TARGET'] ==1].TARGET.count()
total_cnt = cust_df.TARGET.count()
print('unsatisfied 비율은 {0:.2f}'.format((unsatisfied_cnt/total_cnt)))[Out]
0 73012
1 3008
Name: TARGET, dtype: int64
unsatisfied 비율은 0.04- TARGET의 값의 분포가 원본 데이터에서 전체 데이터의 0.04(4%)의 불만족 값(값1)이다.
- 학습과 테스트 데이터셋을 만든 후에도 이와 분포가 비슷한지 확인해야 한다.
# 각 피처의 값 분포 알아보기
cust_df.describe()[Out]
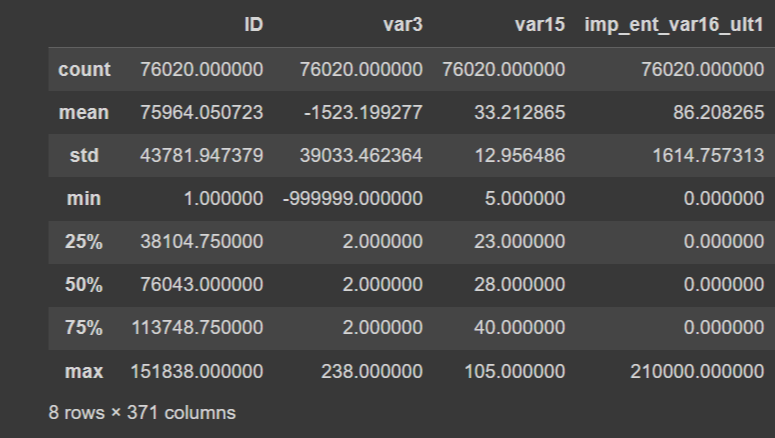
- var3칼럼의 겨우, min의 값이 -99999이다. NaN이나 특정 예외값을 -99999로 변환한 것으로 보인다.
print(cust_df.var3.value_counts()[:10])[Out]
2 74165
8 138
-999999 116
9 110
3 108
1 105
13 98
7 97
4 86
12 85
Name: var3, dtype: int64특이점이 있어보이는 var3컬럼의 value_counts 결과를 보니 -99999에 해당하는 값이 116개나 있다. 제일 많은 값인 2로 다 바꾸어주자.
# NaN이나 특정 예외값이 변환된 것으로 보이는 -99999를 가장 값이 많은 2로 변환
# ID 피처는 단순 식별자이기 때문에 피처 드롭
cust_df['var3'].replace(-99999,2,inplace=True)
cust_df.drop('ID',axis=1,inplace=True)# 클래스 데이터와 피처 데이터 셋을 분리해 별도의 데이터셋으로 저장
X_features = cust_df.iloc[:, :-1]
y_labels = cust_df.iloc[:, -1]
print('피처 데이터 shape:{0}'.format(X_features.shape))[Out]
피처 데이터 shape:(76020, 369)train_test_split()
# 학습 데이터셋과 테스트 데이터셋으로 분리하자.
# 비대칭 데이터셋이기 때문에, Target 값 분포도가 학습 데이터와 테스트 데이터셋에 모두 비슷하게 추출되었는지 확인
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_features, y_labels, test_size=0.2,
random_state=0)
train_cnt = y_train.count()
test_cnt = y_test.count()
print('학습 세트 Shape:{0}, 테스트 세트 Shape:{1}'.format(X_train.shape,X_test.shape))
print('학습 세트 레이블 값 분포 비율')
print(y_train.value_counts()/train_cnt)
print('\n 테스트 세트 레이블 값 분포 비율')
print(y_test.value_counts()/test_cnt)[Out]
학습 세트 Shape:(60816, 369), 테스트 세트 Shape:(15204, 369)
학습 세트 레이블 값 분포 비율
0 0.960964
1 0.039036
Name: TARGET, dtype: float64
테스트 세트 레이블 값 분포 비율
0 0.9583
1 0.0417
Name: TARGET, dtype: float64- 학습과 테스트 데이터셋 모두 TARGET의 값의 분포가 원본 데이터와 유사하게 전체 데이터의 4%정도의 불만족 값(값 1)으로 만들어졌다.
XGBoost 모델 학습과 하이퍼 파라미터 튜닝
- XGBoost의 학습 모델을 생성하고, 예측 결과를 ROC AUC로 평가해보자. 사이킷런 래퍼인 XGBClassifier 기반으로 학습 수행
- n_estimators는 500으로 하되, early_stopping_rounds는 100으로 설정하자.
- 성능 평가 기준이 ROC-AUC이므로, XGBClassifier의 eval_metric은 'auc'로 하자. (logloss로 해도 무관)
- 평가 데이터셋은 앞에서 분리한 테스트 데이터셋을 이용하자.
- 테스트 데이터셋을 XGBoost의 평가 데이터셋으로 사용하면 과적합의 가능성을 증가시킬 수 있으니 알아두자.
- eval_set=[(X_train, y_train), (X_test, y_test)]으로 설정하자.
from xgboost import XGBClassifier
from sklearn.metrics import roc_auc_score
xgb_clf = XGBClassifier(n_estimators=500,random_state=156)
xgb_clf.fit(X_train , y_train, early_stopping_rounds=100,
eval_metric="auc",
eval_set=[(X_train,y_train),(X_test,y_test)])
xgb_roc_score = roc_auc_score(y_test, xgb_clf.predict_proba(X_test)[:, 1], average='macro')
print('ROC AUC: {0:.4f}'.format(xgb_roc_score))[Out]
[0] validation_0-auc:0.799928 validation_1-auc:0.803548
Multiple eval metrics have been passed: 'validation_1-auc' will be used for early stopping.
Will train until validation_1-auc has not improved in 100 rounds.
[1] validation_0-auc:0.802222 validation_1-auc:0.805222
[2] validation_0-auc:0.80819 validation_1-auc:0.813162
[3] validation_0-auc:0.8127 validation_1-auc:0.813243
.
.
.
[247] validation_0-auc:0.870705 validation_1-auc:0.841473
[248] validation_0-auc:0.870771 validation_1-auc:0.841524
[249] validation_0-auc:0.870793 validation_1-auc:0.841477
Stopping. Best iteration:
[149] validation_0-auc:0.862076 validation_1-auc:0.842368
ROC AUC: 0.8424테스트 데이터셋으로 예측시 ROC AUC는 약 0.8424이다.
이제 XGBoost의 하이퍼 파라미터 튜닝을 수행해보자.
- 칼럼의 개수가 많으므로 과적합 가능성을 가정하기
- max_depth, min_child_weight, colsample_bytree 하이퍼 파라미터만 일차 튜닝 대상으로
- 학습 시간이 많이 필요한 ML 모델의 경우, 하이퍼 파라미터 튜닝시 첫 번째로 먼저 2~3개 정도의 파라미터를 결합해 최적 파라미터를 찾아낸 뒤에 이 최적 파라미터를 기반으로 다시 1~2개 파라미터를 결합해 튜닝 수행하기.
- 다음 예제 코드는 8개의 하이퍼 파라미터의 경우의 수를 가져 시간이 오래걸림 (n_estimators는 100으로 줄이고, early_stopping_rounds도 30으로 줄여서 테스트 한 후, 다시 증가시키자.)
- GridSearchCV 적용 후 최적 파라미터가 어떤 것이고, GridSearchCV에 재학습된 Estimator에서 ROC-AUC 수치가 어떻게 향상됐는지 확인
# 하이퍼 파라미터 튜닝
from sklearn.model_selection import GridSearchCV
# 수행 속도 향상을 위해 n_estimators를 100으로 감소
xgb_clf = XGBClassifier(n_estimators=100,random_state=100)
params = {'max_depth':[5,7],'min_child_weight':[1,3],'colsample_bytree':[0.5,0.75]}
#cv는 3으로 지정
gridcv = GridSearchCV(xgb_clf, param_grid=params, cv=3)
gridcv.fit(X_train, y_train, early_stopping_rounds=30, eval_metric="auc",
eval_set=[(X_train, y_train), (X_test, y_test)])
print('GridSearchCV 최적 파라미터:', gridcv.best_params_)
xgb_roc_score = roc_auc_score(y_test, gridcv.predict_proba(X_test)[:, 1], average='macro')
print('ROC AUC {0:.4f}'.format(xgb_roc_score))[Out]
[0] validation_0-auc:0.717265 validation_1-auc:0.725549
Multiple eval metrics have been passed: 'validation_1-auc' will be used for early stopping.
Will train until validation_1-auc has not improved in 30 rounds.
[1] validation_0-auc:0.729887 validation_1-auc:0.738803
[2] validation_0-auc:0.733158 validation_1-auc:0.741697
[3] validation_0-auc:0.738342 validation_1-auc:0.74386
.
.
.
[72] validation_0-auc:0.87511 validation_1-auc:0.842514
[73] validation_0-auc:0.875811 validation_1-auc:0.842654
Stopping. Best iteration:
[43] validation_0-auc:0.864937 validation_1-auc:0.843052
GridSearchCV 최적 파라미터: {'colsample_bytree': 0.75, 'max_depth': 5, 'min_child_weight': 3}
ROC AUC 0.8431- 이전 예제의 ROC AUC가 0.8424에서 'colsample_bytree':0.75, 'max_depth':5, 'min_child_weight':3로 하이퍼 파라미터를 적용한 후, 0.8431로 개선되었으나, 아주 작은 차이이다.
- 앞서 구한 최적화 하이퍼 파라미터를 기반으로, 다른 하이퍼 파라미터를 변경 또는 추가해 다시 최적화를 진행해보자.
- 최적 파라미터 3가지를 적용한 뒤,
- n_estimators=1000으로 증가시키고,
- learning_rate는 0.02로 감소시키고,
- reg_alpha=0.03을 추가해보자.
- 그 후 다시 XGBClassifier를 학습시킨 뒤, ROC AUC를 구하자.
xgb_clf = XGBClassifier(n_estimators=1000,random_state=156,
learning_rate=0.02, max_depth=5,
min_child_weight=3, colsample_bytree=0.75, reg_alpha=0.03)
# 학습 수행
xgb_clf.fit(X_train, y_train, early_stopping_rounds=200,
eval_metric="auc", eval_set=[(X_train, y_train), (X_test, y_test)])
xgb_roc_score = roc_auc_score(y_test, xgb_clf.predict_proba(X_test)[:, 1],average='macro')
print('ROC AUC: {0:.4f}'.format(xgb_roc_score))[0] validation_0-auc:0.817376 validation_1-auc:0.812993
Multiple eval metrics have been passed: 'validation_1-auc' will be used for early stopping.
Will train until validation_1-auc has not improved in 200 rounds.
[1] validation_0-auc:0.819701 validation_1-auc:0.813427
[2] validation_0-auc:0.823292 validation_1-auc:0.818083
[3] validation_0-auc:0.825727 validation_1-auc:0.82164
.
.
.
[420] validation_0-auc:0.878097 validation_1-auc:0.843611
[421] validation_0-auc:0.878127 validation_1-auc:0.843597
Stopping. Best iteration:
[221] validation_0-auc:0.865092 validation_1-auc:0.844718
ROC AUC: 0.8447- 0.8431에서 0.8447으로 살짝 향상된 결과를 보인다.
- XGBoost가 GBM보다는 빠르나, 여전히 수행시간이 길다는 점이 단점
- 따라서 하이퍼 파라미터를 나열해 튜닝하면 너무 오래걸림
- 앙상블 계열 알고리즘은 과적합이나 잡음에 기본적으로 뛰어나기 대문에 하이퍼 파라미터 튜닝으로 성능 수치 개선이 급격히 되는 경우가 많지는 않다.
튜닝된 모델에서 각 피처의 중요도를 피처 중요도 그래프로 나타내보자.
from xgboost import plot_importance
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(1,1,figsize=(10,8))
plot_importance(xgb_clf, ax=ax, max_num_features=20, height=0.4)[Out]
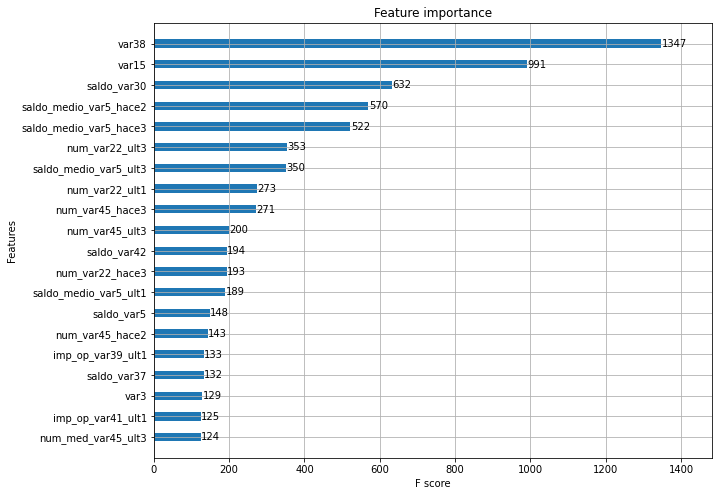
- XGBoost의 예측 성능을 좌우하는 가장 중요한 피처는 var38, var15순이다.
LightGBM 모델 학습과 하이퍼 파라미터 튜닝
- 앞의 XGBoost 예제코드의 데이터셋을 기반으로 LightGBM으로 학습을 수행하고 ROC-AUC를 측정해보자.
- 동일하게 n_estimators=500, early_stopping_rounds=100, 평가 데이터셋은 테스트 데이터셋, eval_metric=auc로 설정
from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=500)
evals=[(X_test, y_test)]
lgbm_clf.fit(X_train, y_train, early_stopping_rounds=100, eval_metric="auc", eval_set=evals,
verbose=True)
lgbm_roc_score = roc_auc_score(y_test, lgbm_clf.predict_proba(X_test)[:, 1], average='macro')
print('ROC AUC: {0:.4f}'.format(lgbm_roc_score))[Out]
[1] valid_0's binary_logloss: 0.165046 valid_0's auc: 0.817384
Training until validation scores do not improve for 100 rounds.
[2] valid_0's binary_logloss: 0.16 valid_0's auc: 0.81863
[3] valid_0's binary_logloss: 0.15628 valid_0's auc: 0.827229
.
.
.
123] valid_0's binary_logloss: 0.140184 valid_0's auc: 0.836706
[124] valid_0's binary_logloss: 0.140243 valid_0's auc: 0.836456
[125] valid_0's binary_logloss: 0.140297 valid_0's auc: 0.836177
Early stopping, best iteration is:
[25] valid_0's binary_logloss: 0.139888 valid_0's auc: 0.839655
ROC AUC: 0.8397- Light GBM 수행 결과 ROC AUC는 0.8397이며, 앞의 XGBoost보다 훨씬 시간이 적게 걸린다.
- 좀 더 다양한 하이퍼 파라미터를 튜닝해보자. 튜닝 대상은 num_leaves/ max_depth/ min_child_samples/ subsample
from sklearn.model_selection import GridSearchCV
# 수행 속도 향상을 위해 n_estiimators=200으로 감소
lgbm_clf = LGBMClassifier(n_estimators=200)
params={'num_leaves':[32,64],'max_depth':[128,160],'min_child_samples':[60,100],
'subsample':[0.8,1]}
# cv는 3으로 지정
gridcv = GridSearchCV(lgbm_clf, param_grid=params, cv=3)
gridcv.fit(X_train, y_train, early_stopping_rounds=30, eval_metric="auc",
eval_set=[(X_train, y_train), (X_test, y_test)])
print('GridSearchCV 최적 파라미터:', gridcv.predict_proba(X_test)[:, 1], average='macro')
print('ROC AUC: {0:.4f}'.format(lgbm_roc_score))[Out]
[1] valid_0's binary_logloss: 0.156085 valid_0's auc: 0.820235 valid_1's binary_logloss: 0.164992 valid_1's auc: 0.81613
Training until validation scores do not improve for 30 rounds.
[2] valid_0's binary_logloss: 0.150951 valid_0's auc: 0.825778 valid_1's binary_logloss: 0.159874 valid_1's auc: 0.821835
[3] valid_0's binary_logloss: 0.147167 valid_0's auc: 0.832192 valid_1's binary_logloss: 0.156391 valid_1's auc: 0.827305
.
.
.
[51] valid_0's binary_logloss: 0.118036 valid_0's auc: 0.895359 valid_1's binary_logloss: 0.13844 valid_1's auc: 0.842349
[52] valid_0's binary_logloss: 0.11788 valid_0's auc: 0.895964 valid_1's binary_logloss: 0.138404 valid_1's auc: 0.842547
Early stopping, best iteration is:
[22] valid_0's binary_logloss: 0.126309 valid_0's auc: 0.871544 valid_1's binary_logloss: 0.139253 valid_1's auc: 0.844171
GridSearchCV 최적 파라미터: {'max_depth': 128, 'min_child_samples': 100, 'num_leaves': 32, 'subsample': 0.8}
ROC AUC: 0.8442
최적 하이퍼 파라미터 max_depth=128, min_child_samples=100, num_leaves=32, subsample=0.8을 적용한 후 재 학습히키고 ROC AUC를 측정하자.
# 최적 하이퍼 파라미터 적용 후 재 학습
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=32, subsample=0.8,
min_child_samples=100, max_depth=128)
evals = [(X_test, y_test)]
lgbm_clf.fit(X_train, y_train, early_stopping_rounds=100, eval_metric="auc",
eval_set=evals, verbose=True)
lgbm_roc_score = roc_auc_score(y_test, lgbm_clf.predict_proba(X_test)[:, 1],
average='macro')
print('ROC AUC: {0:.4f}'.format(lgbm_roc_score))[Out]
[1] valid_0's binary_logloss: 0.165016 valid_0's auc: 0.819488
Training until validation scores do not improve for 100 rounds.
[2] valid_0's binary_logloss: 0.159711 valid_0's auc: 0.822387
[3] valid_0's binary_logloss: 0.156068 valid_0's auc: 0.829542
.
.
.
[120] valid_0's binary_logloss: 0.13949 valid_0's auc: 0.8397
[121] valid_0's binary_logloss: 0.139455 valid_0's auc: 0.839924
[122] valid_0's binary_logloss: 0.139489 valid_0's auc: 0.839844
Early stopping, best iteration is:
[22] valid_0's binary_logloss: 0.139253 valid_0's auc: 0.844171
ROC AUC: 0.8442- Light GBM의 경우 테스트 데이터셋에서 ROC AUC가 0.8442으로 측정되었다.
4-9. 캐글 신용카드 사기 검출 분류 실습
- 해당 데이터 셋의 레이블인 Class 속성은 매우 불균형한 분포를 가지고있다.
- class는 0과 1으로, 0은 사기가 아닌 정상적인 신용카드 트랜잭션 데이터, 1은 신용카드 사기 트랜잭션을 의미
- 전체 데이터의 약 0.172%만이 레이블 값이 1(사기 트랜잭션)이다.
- 사기 검출이나 이상 검출과 같은 데이터셋은 레이블 값이 극도로 불균형한 분포를 가지기 쉽다. (이상현상의 비중↓)
언더 샘플링과 오버 샘플링의 이해


- 이상 레이블을 가지는 데이터 건수가 정상 레이블을 가진 데이터 건수에 비해 너무 적을 때 예측 성능에 문제 발생, 데이터 건수가 적다는 것은 제대로 다양한 유형을 학습하지 못한다는 의미
- 불균형한 레이블 값 분포로 인한 문제점 해결을 위해 적절한 학습 데이터를 확보하는 방안
- 오버 샘플링
- 예측 성능상 언더 샘플링보다 더 유리한 경우가 많다.
- 적은 레이블을 가진 데이터 셋을 많은 레이블을 가진 데이터 셋 수준으로 증식
- 일반적으로 적은 이상 데이터셋을 증식하여 학습을 위한 충분한 데이터 확보
- 동일한 데이터를 단순히 증식하는 방법은 과적합이 되기 때문에 의미가 없기 때문에, 원본 데이터의 피처 값들을 약간만 변경하여 증식한다. EX. 대표적으로 SMOTE 방법이 있다.(Synthetic Minority Over-sampling Technique)
- Smote : 적은 데이터셋에 있는 개별 데이터들의 K 최근접 이웃을 찾아서 이 데이터와 K개 이웃들의 차이를 일정값으로 만들어, 기존 데이터와 약간 차이가 나는 새로운 데이터를 생성하는 방식
- smote를 구현한 대표적 파이썬 패키지는 imbalanced-learn
- 언더 샘플링
- 많은 레이블을 가진 데이터셋을 적은 레이블을 가진 데이터셋 수준으로 감소
- 일반적으로 많은 정상 레이블 데이터 건수를 줄이는 방법
- (-) 너무 많은 정상 레이블 데이터를 감소시키기 때문에 정상 레이블의 경우 오히려 제대로된 학습 수행 X
- 오버 샘플링
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline
card_df = pd.read_csv('/content/creditcard.csv')
card_df.head(3)[Out]

- creditcard.csv의 V로 시작하는 피처들의 의미는 알 수가 없다.
- Time 피처의 경우 데이터 생성 관련한 작업용 속성으로 큰 의미가 없기에 제거하자.
- Amount 피처는 신용카드 트랜잭션 금액을 의미하며, Class는 레이블로서 0의 경우 정상, 1의 경우 사기 트랜잭션
- card_df.info()로 확인해보면 284,807개의 레코드 중 결측치는 없고, class 레이블만int, 나머지는 float형이다.
인자로 입력된 DataFrame을 복사한 뒤, 이를 가공하여 반환하는 get_preprocessed_df() 함수와 데이터 가공 후 학습/테스트 데이터셋을 반환하는 get_train_test_df() 함수를 생성하자.
from sklearn.model_selection import train_test_split
#인자로 받은 df 복사 후, time 칼럼만 삭제 후 복사된 df 반환
def get_preprocessed_df(df=None):
df_copy = df.copy()
df_copy.drop('Time', axis=1, inplace=True)
return df_copy# 사전 데이터 가공 후 학습/테스트 데이터셋을 반환하는 함수 생성
def get_train_test_dataset(df=None):
# 인자로 입력된 df의 사전 데이터 가공이 완료된 복사 df 반환
df_copy = get_preprocessed_df(df)
# df의 맨 마지막 칼럼=label, 나머지=feature
X_features = df_copy.iloc[:, :-1]
y_target = df_copy.iloc[:, -1]
# train_test_split()으로 학습/테스트 데이터셋 분할, stratify=y_target으로 stratified 기반 분할
X_train, X_test, y_train, y_test = \
train_test_split(X_features, y_target, test_size=0.3, random_state=0, stratify=y_target)
# 학습과 데이터 셋 반환
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)# 생성한 학습 데이터셋과 테스트 데이터셋의 레이블 값 비율을 백분율로 환산해서
# 비슷하게 분할되었는지 확인
print('학습 데이터 레이블 값 비율')
print(y_train.value_counts() / y_train.shape[0] * 100)
print(y_test.value_counts() / y_test.shape[0] * 100)[Out]
학습 데이터 레이블 값 비율
0 99.827451
1 0.172549
Name: Class, dtype: float64
0 99.826785
1 0.173215
Name: Class, dtype: float64이제 모델을 만들어보자. 먼저 로지스틱 회귀를 이용해 신용 카드 사기 여부를 예측해보자.
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrix
from sklearn.metrics import recall_score, f1_score, roc_curve, roc_auc_score
# 평가 단원에서 생성했던 get_clf_eval() 함수 사용
def get_clf_eval(y_test, pred=None, pred_proba=None):
# roc_auc가 예측 확률값 기반으로 계산될 수 있도록 인자를 pred=None, pred_proba=None으로 변경
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
f1 = f1_score(y_test, pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}, \
F1 : {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))from sklearn.linear_model import LogisticRegression
lr_clf = LogisticRegression()
lr_clf.fit(X_train, y_train)
lr_pred = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:, 1]
get_clf_eval(y_test, lr_pred, lr_pred_proba)[Out]
오차 행렬
[[85283 12]
[ 59 89]]
정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014, F1 : 0.7149, AUC:0.9727- 테스트 데이터 셋으로 측정시 재현율(Recall)이 0.6014, ROC AUC가 0.9727이다.
이번에는 LightGBM을 이용한 모델을 만들어보자.(+ 반복적인 작업 수행 과정을 함수로 만들어놓자)
def get_model_train_eval(model, ftr_train=None, ftr_test = None, tgt_train=None, tgt_test=None):
model.fit(ftr_train, tgt_train)
pred = model.predict(ftr_test)
pred_proba = model.predict_proba(ftr_test)[:, 1]
get_clf_eval(tgt_test, pred, pred_proba)*주의

from lightgbm import LGBMClassifier
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1,
boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train,
tgt_test=y_test)[Out]
오차 행렬
[[85290 5]
[ 35 113]]
정확도: 0.9995, 정밀도: 0.9576, 재현율: 0.7635, F1 : 0.8496, AUC:0.9786- 재현율 0.7635, 정확도 0.9995로 앞의 로지스틱 회귀보다는 높은 수치를 나타낸다.
데이터 분포도 변환 후 모델 학습-예측-평가
- 이번에는 왜곡된 분포도를 가지는 데이터를 재가공한 뒤 모델을 다시 테스트해보자.
- 중요 피처 값의 분포를 먼저 살펴보자.
- 로지스틱 회귀는 선형 모델이기 때문에, 선형 모델은 중요 피처들의 값이 정규 분포형태를 유지하는 것을 선호한다.
- Amount피처는 신용 카드사용 금액으로 정상/사기 트랜잭션을 결정하는 매우 중요한 속성일 가능성이 높다. Amount 피처의 분포도를 확인해보자.
import seaborn as sns
plt.figure(figsize=(8,4))
plt.xticks(range(0, 30000, 1000), rotation=60)
sns.distplot(card_df['Amount'])
1000불 이하인 데이터가 대부분이며, 27,000불까지 드물지만 많은 금액을 사용한 경우가 발생하여, 꼬리가 긴 형태의 분포 곡선을 가지고 있다.
Amount 피처를 표준 정규분포 형태로 변환한 뒤에, 로지스틱 회귀의 예측 성능을 측정해보자. (get_processed_df() 함수 사용, 함수를 사이킷런의 StandardScaler 클래스를 이용해 Amount 피처를 정규분포 형태로 변환하는 코드로 변경)
from sklearn.preprocessing import StandardScaler
# 사이킷런의 StandardSclaer를 이용해 정규 분포 형태로 Amount 피처 값 변환하는 로직으로 수정
def get_preprocessed_df(df=None):
df_copy = df.copy()
scaler = StandardScaler()
amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1,1))
# 변환된 Amount를 Amount_scaled로 피처명 변경 후, Dataframe 맨 앞 컬럼으로 입력
df_copy.insert(0, 'Amount_Scaled', amount_n)
# 기존 Time, Amount 피처 삭제
df_copy.drop(['Time', 'Amount'], axis=1, inplace=True)
return df_copy# Amount를 정규분포 형태로 변환 후, 로지스틱 회귀 및 Light GBM수행
X_train ,X_test, y_train, y_test = get_train_test_dataset(card_df)
print('## 로지스틱 회귀 예측 성능 ##')
lr_clf = LogisticRegression()
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train,
tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train,
tgt_test=y_test)[Out]
## 로지스틱 회귀 예측 성능 ##
오차 행렬
[[85281 14]
[ 58 90]]
정확도: 0.9992, 정밀도:0.8654, 재현율: 0.6081
### LightGBM 예측 성능 ###
오차 행렬
[[85263 32]
[ 107 41]]
정확도: 0.9984, 정밀도:0.5616, 재현율: 0.2770- 정규 분포 형태로 Amount 피처 값을 변환한 후 , 테스트 데이터셋에 적용한 로지스틱 회귀 및 LightGBM 두 모델 모두 변환 이전과 비교해 성능이 크게 개선되지는 않았다.
이번에는 StandardScaler가 아니라, 로그 변환을 수행해보자.
- 로그 변환은 데이터 분포도가 심하게 왜곡되어 있을 경우 적용하는 중요 기법 중 하나.
- 원래 값을 log값으로 변환해 원래 큰 값을 상대적으로 작은 값으로 변환하기 대문에, 데이터 분포도의 왜곡을 상당 수준 개선해준다.
- log1p() 함수 이용 (앞서 만든 함수를 로그 변환 로직으로 변경)
def get_preprocessed_df(df=None):
df_copy =df.copy()
# 넘파이의 log1p()를 이용해 Amount를 로그 변환
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0, 'Amount_Scaled', amount_n)
df_copy.drop(['Time', 'Amount'], axis=1, inplace=True)
return df_copyX_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('## 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train,
tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train,
tgt_test=y_test)[Out]
## 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85283 12]
[ 59 89]]
정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014, F1 : 0.7149, AUC:0.9727
### LightGBM 예측 성능 ###
오차 행렬
[[85290 5]
[ 35 113]]
정확도: 0.9995, 정밀도: 0.9576, 재현율: 0.7635, F1 : 0.8496, AUC:0.9786- 두 모델 모두 정밀도, 재현율, ROC AUC에서 약간씩 성능이 개선되었음을 나타내고 있다.
이상치 데이터 제거 후 모델 학습-예측-평가
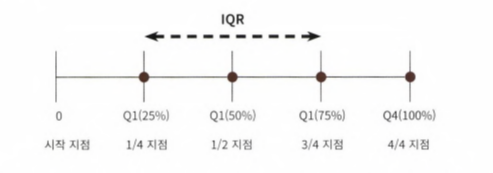

- 이상치를 찾는 방법 중 IQR 방식을 적용해보자. 사분위 편차를 이용하는 방법으로, 흔히 박스 플롯으로 시각화 가능
- IQR을 이용해 이상치 데이터를 검출하는 방식은 보통 IQR에 1.5를 곱해서 생성된 범위를 이용해 최댓값과 최솟값을 결정한 뒤, 초과하거나 미달하는 데이터를 이상치로 간주하는 것
이상치 데이터를 IQR을 이용해 제거해보자.
- 먼저 어떤 피처의 이상치 데이터를 검출한 것인지 선택해야 한다. 많은 피처가 있을 경우, 이들 중 결정값(즉 레이블)과 가장 상관성이 높은 피처를 위주로 이상치를 검출하는 것이 좋다.
- DataFrame의 corr()을 이용해 각 피처별로 상관도를 구한 뒤, seaborn의 heatmap으로 시각화해보자.
import seaborn as sns
plt.figure(figsize=(9,9))
corr = card_df.corr()
sns.heatmap(corr, cmap='RdBu')[Out]
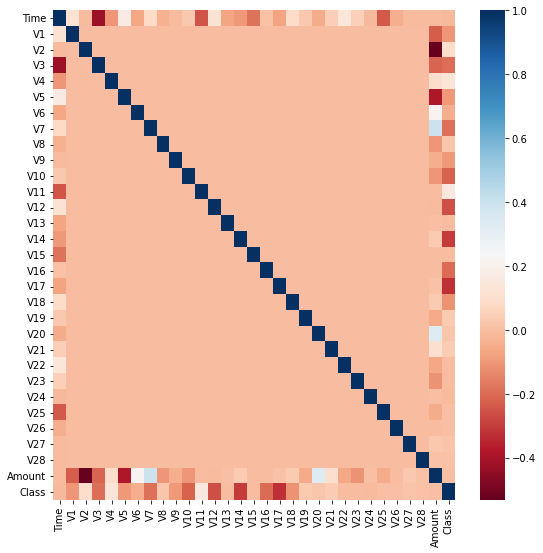
- 상관관계 히트맵에서 cmap='RdBu'로 설정해, 양의 상관관계가 높을 수록 진한 파란색에, 음의 상관관계가 높을 수록 진한 빨간색에 가깝게 표현되었다.
- 상관관계 히트맵에서 맨 아래에 위치한 결정 레이블인 Class 피처와 음의 상관관계가 가장 높은 피처는 V14와 V17이다.
- 이 중 V14에 대해서만 이상치를 찾아서 제거해보자.
- IQR을 이용해 이상치를 검출하는 함수를 생성, 검출한 이상치를 삭제
- get_outlier() 함수는 인자로 DataFrame과 이상치를 검출한 칼럼을 입력받는다.
- 함수 내에서 넘파이의 percentile()을 이용해 1/4분위와 3/4 분위를 구하고, 이에 기반해 IQR을 계산
- 계산된 IQR에 1.5를 곱해서 최댓값과 최솟값 지점을 구한 뒤, 최댓값보다 크거나 최솟값보다 작은 값을 이상치로 설정, 해당 이상치가 있는 DataFrame 반환
import numpy as np
def get_outlier(df=None, column=None, weight=1.5):
# fraud에 해당하는 column 데이터만 추출, 1/4 분위와 3/4 분위 지점을 np.percentile로 구함
fraud = df[df['Class']==1][column]
quantile_25 = np.percentile(fraud.values,25)
quantile_75 = np.percentile(fraud.values, 75)
# IQR을 구하고, IQR에 1.5 곱해서 최소,최댓값 지점 구하기
iqr = quantile_75 - quantile_25
iqr_weight = iqr * weight
lowest_val = quantile_25 - iqr_weight
highest_val = quantile_75 + iqr_weight
# 최댓값보다 크거나, 최솟값보다 작은 값을 이상치 데이터로 설정하고, df index 반환
outlier_index = fraud[(fraud<lowest_val) | (fraud>highest_val)].index
return outlier_indexoutlier_index = get_outlier(df=card_df, column='V14', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)[Out]
이상치 데이터 인덱스: Int64Index([8296, 8615, 9035, 9252], dtype='int64')총 4개의 데이터인 8296, 8615, 9035, 9252번 index가 이상치로 추출되었다.
get_outlier()를 이용해 이상치를 추출하고 이를 삭제하는 로직을 get_processed_df() 함수에 추가해 데이터를 가공한 후에, 이 데이터셋으로 로지스틱 회귀와 Light GBM 모델을 다시 적용해보자.
# get_processed_df()를 로그 변환 후, V14 피처의 이상치 데이터를 삭제하는 로직으로 변경
def get_preprocessed_df(df=None):
df_copy = df.copy()
amount_n = np.log1p(df_copy['Amount'])
df_copy.insert(0, 'Amount_Scaled', amount_n)
#이상치 데이터 삭제 로직 추가
outlier_index = get_outlier(df=df_copy, column='V14', weight=1.5)
df_copy.drop(outlier_index, axis=0, inplace=True)
return df_copyX_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train = X_train, ftr_test = X_test, tgt_train=y_train,
tgt_test = y_test)
print('### Light GBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train,
tgt_test=y_test)[Out]
### 로지스틱 회귀 예측 성능 ###
오차 행렬
[[85277 18]
[ 51 95]]
정확도: 0.9992, 정밀도: 0.8407, 재현율: 0.6507, F1 : 0.7336, AUC:0.9327
### Light GBM 예측 성능 ###
오차 행렬
[[85291 4]
[ 26 120]]
정확도: 0.9996, 정밀도: 0.9677, 재현율: 0.8219, F1 : 0.8889, AUC:0.9820- 이상치 제거후 , 로지스틱 회귀와 Light GBM 모두 예측 성능이 크게 향상되었다.
- 로지스틱 회귀는 재현율이 60.14에서 0.6507로, LightGBM의 경우 0.7635에서 0.8219로 크게 증가하였다.
SMOTE 오버 샘플링 적용 후 모델 학습-예측-평가
- imbalanced-learn 패키지의 SMOTE 클래스로 간단하게 구현가능하다.
- smote 적용시 반드시 학습 데이터셋만 오버 샘플링해야함에 주의하자. 검증 데이터셋이나 테스트 데이터셋을 오버샘플링할 경우, 결국은 원본 데이터가 아닌 데이터셋에서 검증/테스트를 수행하기 때문에 올바른 검증/테스트가 될 수 X
- 앞 예제에서 생성한 학습 피처/레이블 데이터를 SMOTE 객체의 fit_sample() 메소드로 증식한뒤, 데이터를 비교해보자.
from imblearn.over_sampling import SMOTE
smote = SMOTE(random_state=0)
X_train_over, y_train_over = smote.fit_resample(X_train, y_train)
print('SMOTE 적용 전 학습용 피처/레이블 데이터셋:', X_train.shape, y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터셋:', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 후 레이블 값 분포: \n',
pd.Series(y_train_over).value_counts())* 책처럼 smote.fit_sample() 입력했더니 에러가 났다. fit_resample()로 바꿔서 적용하면 실행된다.
[Out]
SMOTE 적용 전 학습용 피처/레이블 데이터셋: (199362, 31) (199362,)
SMOTE 적용 후 학습용 피처/레이블 데이터셋: (398040, 31) (398040,)
SMOTE 적용 후 레이블 값 분포:
0 199020
1 199020
Name: Class, dtype: int64- SMOTE 적용 이전 학습용 데이터셋은 199,362건이었지만, 2배에 가까운 398,040건으로 증식되었다.
- 그리고 SMOTE 적용 후 레이블 값이 0과 1의 분포가 동일하게 199,020건으로 생성되었다.
이제 이렇게 생성된 학습 데이터셋을 기반으로 먼저 로지스틱 회귀 모델을 학습한 뒤, 성능을 평가해보자.
lr_clf = LogisticRegression()
# ftr_train과 tgt_train 인자값이 SMOTE 증식된 X_train_over과 y_train_over로 변경됨에 유의
get_model_train_eval(lr_clf, ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over,
tgt_test=y_test)[Out]
오차 행렬
[[83468 1827]
[ 12 134]]
정확도: 0.9785, 정밀도: 0.0683, 재현율: 0.9178, F1 : 0.1272, AUC:0.9749- 로지스틱 회귀 모델의 경우 재현율이 91.78%로 크게 증가하였지만, 정밀도가 6.83%로 급격하게 저하되었다. 재현율이 높더라도 이정도로 저조한 정밀도로는 현실 업무에 적용할 수 없다.
- 이는 로지스틱 회귀모델이 오버 샘플링으로 인해 실제 원본데이터의 유형보다 너무나 많은 Class=1 데이터를 학습하면서 실제 테스트 데이터셋에서 예측을 지나치게 Class=1로 적용하여, 정밀도가 급격히 떨어지게 된 것이다.(정밀도는 예측을 긍정으로 한게 일치한 정도)
- 분류 결정 임곗값에 따른 정밀도와 재현율 곡선을 통해 SMOTE로 학습된 로지스틱 회귀모델에 발생한 문제를 확인해보자. 3장(평가)에서 사용했던 precision_recall_curve_plot() 함수 이용
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
from sklearn.metrics import precision_recall_curve
def precision_recall_curve_plot(y_test, pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출
precisions, recalls, thresholds = precision_recall_curve (y_test, pred_proba_c1)
# X축을 threshold 값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행,정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary], label='recall')
# threshold 값 X축의 Scale을 0.1단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot ( y_test, lr_clf.predict_proba(X_test)[:, 1])[Out]

- 임곗값이 0.99 이하에서는 recall(주황색)이 매우 좋고, precision(파란색)이 극단적으로 낮다가, 0.99 이상에서는 반대로 recall이 매우 낮고, precision이 높아진다.
- 분류 결정 임곗값을 조정하더라도, 임계값의 민감도가 너무 심해서 올바른 재현율/정밀도 성능을 얻을 수 없다.
- 그러므로 로지스틱 회귀 모델의 경우, SMOTE 적용 후 올바른 예측 모델이 생성되지 못하였다.
이번에는 LightGBM 모델을 SMOTE로 오버 샘플링된 데이터 셋으로 학습-예측-평가를 수행해보자.
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1,
boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train_over, ftr_test=X_test,
tgt_train=y_train_over, tgt_test=y_test)[Out]
오차 행렬
[[85285 10]
[ 25 121]]
정확도: 0.9996, 정밀도: 0.9237, 재현율: 0.8288, F1 : 0.8736, AUC:0.9797
- 재현율이 이상치만 제거한 경우인 82.19%와 비교했을 때 82.88%로 조금 향상되었다.
- 그러나 정밀도는 96.77%에서 92.37%로 조금 줄어들었다.
- SMOTE를 적용하면 재현율(실제값이 긍정인 것 중 일치하는 정도)은 높아지나, 정밀도(긍정으로 예측한 것 중 일치하는 정도)는 낮아지는 것이 일반적이다.
- 좋은 SMOTE 패키지일 수록 재현율 증가율은 높이고, 정밀도 감소율은 낮출 수 있도록 효과적으로 데이터를 증식한다.
이제까지 이번 예제에서 데이터를 가공한 과정을 정리하면 다음과 같다.

4-10. 스태킹 앙상블
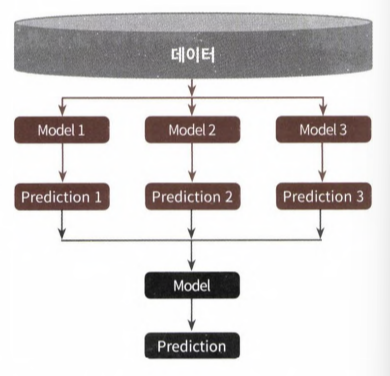
- 스태킹은 개별적인 여러 알고리즘을 결합해 예측 결과를 도출한다는 점에서 배깅과 부스팅과 비슷하다.
- 하지만 차이점은 "개별 알고리즘"으로 예측한 데이터를 기반으로 다시 예측을 수행한다는 것이다. 개별 알고리즘의 예측 결과 데이터셋을 기반으로 다시 최종 예측을 수행하는 방식이다.
- 개별 알고리즘의 예측 결과 데이터셋을 최종적인 메타 데이터셋으로 만들어, 별도의 ml 알고리즘으로 최좋학습을 수행, 테스트 데이터를 기반으로 다시 최종 예측을 수행한다는 점에서 '메타 모델'이라 한다.
- 두 종류의 모델이 필요하다.
- 개별적인 기반 모델
- 이 개별 기반 모델의 예측 데이터를 학습 데이터로 만들어서 학습하는 최종 메타 모델
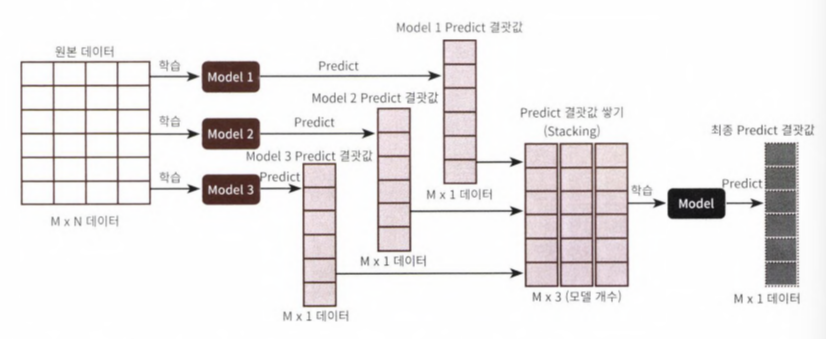
- 스태킹 모델의 핵심은 여러 개별 모델의 예측 데이터를 각각 스태킹 형태로 결합해 최종 메타 모델의 학습용 피처 데이터 셋과 테스트용 피처 데이터셋을 만드는 것
- 많은 개별 모델이 필요하다. 2-3개의 개별 모델의 결합만으로는 예측 성능 향싱시키기 어려움
- 일반적으로 성능이 비슷한 모델을 결합한다.
기본 스태킹 모델 만들기 (위스콘신 암 데이터셋)
import numpy as np
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
cancer_data = load_breast_cancer()
X_data = cancer_data.data
y_label = cancer_data.target
X_train, X_test, y_train, y_test = train_test_split(X_data, y_label, test_size=0.2, random_state=0)# 스태킹에 사용될 개별 ML 모델 생성
knn_clf = KNeighborsClassifier(n_neighbors=4)
rf_clf = RandomForestClassifier(n_estimators=100, random_state=0)
dt_clf = DecisionTreeClassifier()
ada_clf = AdaBoostClassifier(n_estimators=100)
# 스태킹으로 만들어진 데이터셋을 학습, 예측할 최종 모델
lr_final = LogisticRegression(C=10)# 개별 모델 학습
knn_clf.fit(X_train, y_train)
rf_clf.fit(X_train, y_train)
dt_clf.fit(X_train, y_train)
ada_clf.fit(X_train, y_train)# 정확도 측정
knn_pred = knn_clf.predict(X_test)
rf_pred = rf_clf.predict(X_test)
dt_pred = dt_clf.predict(X_test)
ada_pred = ada_clf.predict(X_test)
print('KNN 정확도: {0:.4f}'.format(accuracy_score(y_test, knn_pred)))
print('랜덤 포레스트 정확도 {0:.4f}'.format(accuracy_score(y_test, rf_pred)))
print('결정 트리 정확도 : {0:.4f}'.format(accuracy_score(y_test, dt_pred)))
print('AdBoost 정확도 : {0:.4f}'.format(accuracy_score(y_test, ada_pred)))[Out]
KNN 정확도: 0.9211
랜덤 포레스트 정확도 0.9649
결정 트리 정확도 : 0.9123
AdBoost 정확도 : 0.9561개별 알고리즘으로부터 예측된 예측값을 Column 레벨로 옆으로 붙여서 피처 값으로 만들어, 최종 메타 모델인 로지스틱 회귀에서 학습 데이터로 다시 사용하자.
반환된 데이터셋은 1차원 형태의 ndarray이므로 먼저 반환된 예측 결과를 행 형태로 붙인 뒤, 넘파이의 transpose()를 이용하자.
pred = np.array([knn_pred, rf_pred, dt_pred, ada_pred])
print(pred.shape)# transpose 이용, 행과 열의 위치 바꿔서 column 레벨로 예측결과 피처로 만듦
pred = np.transpose(pred)
print(pred.shape)# 예측 데이터로 생성된 데이터 셋 기반, 최종 메타 모델인 로지스틱 회귀 학습
lr_final.fit(pred, y_test)
final = lr_final.predict(pred)
print('최종 메타 모델의 예측 정확도: {0:.4f}'.format(accuracy_score(y_test, final)))[Out]
최종 메타 모델의 예측 정확도: 0.9737- 정확도가 개별 모델 정확보다 향상되었다.(하지만 항상 스태킹 기법으로 예측한 결과가 개별 모델보다 좋아진다는 보장은 없다.)
과적합 개선을 위한 CV 세트 기반의 스태킹
- 과적합을 개선하기 위해 최종 메타 모델을 위한 데이터셋을 만들 때, 교차 검증 기반으로 예측된 결과 데이터셋을 이용한다.
- 앞 예제에서 마지막에 로지스틱 회귀 모델 기반 최종 학습시에 레이블 데이터셋으로 학습 데이터가 아닌, 테스트용 레이블 데이터셋을 기반으로 학습했기 때문에, 과적합 문제가 발생할 수 있다. → lr_final.fit(pred, y_test)
- 2단계의 스텝으로 구분된다.
- STEP1 : 각 모델별로 원본 학습/테스트 데이터를 예측한 결과 값을 기반으로 메타 모델을 위한 학습용/테스트용 데이터를 생성
- STEP2 : 스텝1에서 개별 모델들이 생성한 학습용 데이터를 모두 스태킹 형태로 합쳐서, 메타 모델이 학습할 최종 학습용 데이터셋을 생성한다. 마찬가지로 각 모델들이 생성한 테스트용 데이터를 모두 스태킹 형태로 합쳐서 메타 모델이 예측할 최종 테스트 데이터셋 생성
STEP1-1

- STEP1의 핵심은 개별 모델에서 메타 모델인 2차 모델에서 사용될 학습용 데이터와 테스트용 데이터를 교차 검증을 통해서 생성하는 것이다. 스텝1은 개별 모델 레벨에서 수행하며, 이러한 로직을 여러 개의 개별 모델에서 동일하게 수행
- 먼저 학습용 데이터를 n개의 fold로 나눈다. 여기서는 3개의 폴드 세트로 가정하자.
- 3개의 폴드세트이므로 3번의 유사한 반복작업을 수행하고, 마지막 3번째 반복에서 개별 모델의 학습 값으로 학습 데이터와 테스트 데이터를 생성한다.
- 주요 프로세스를 정리하자면
- 학습용 데이터를 3개의 폴드로 나누되, 2개의 폴드는 학습을 위한 폴드, 나머지 1개는 검증을 위한 폴드로 나눈다. 이렇게 두 개의 폴드로 나뉜 학습 데이터를 기반으로 개별 모델 학습
- 학습된 개별 모델은 검증 폴드 1개로 예측하고 그 결과를 저장한다.
- 이러한 로직을 3번 반복하면서 학습 데이터와 검증 데이터셋을 변경해가면서 학습 후 예측 결과를 별도로 저장
- 마찬가지로 이러한 로직을 3번 반복하면서 이 예측 값의 평균으로 최종 결괏값 생성, 이를위한 메타 모델을 위한 테스트 데이터셋으로 사용
- 스텝1의 개별 모델이 메타 모델을 위한 학습/테스트 데이터를 생성하는 로직을 순차적으로 설명한 첫번째 그림
STEP1-2

두 번째 그림은 스태킹 데이터를 생성하는 두 번째 반복, 폴드 내의 학습용 데이터를 변경하고 첫 번째 그림과 동일한 작업 수행
STEP1-3
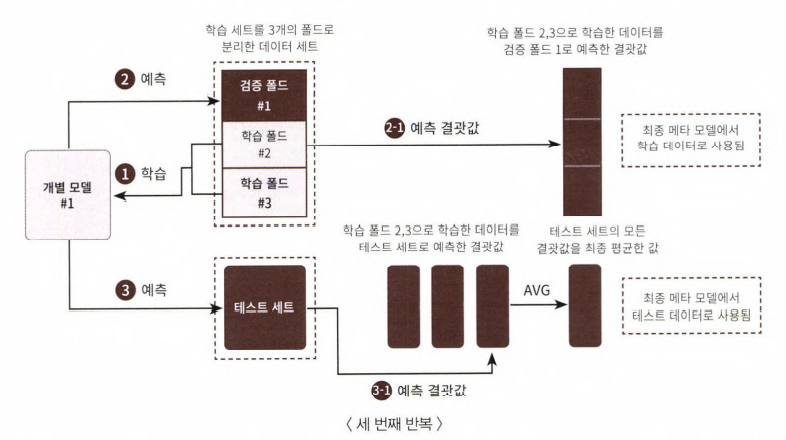
- 세 번째 그림에서 세 번째 반복을 수행하면서 폴드 내의 학습용 데이터 세트가 변경되는 모습을 알 수 있다.
- 3번째까지 완료시,앞서 만들어진 폴드 별 예측 데이터를 합하여 메타 모델에서 사용될 학습 데이터를 만들게 된다.
- 마찬가지로 1,2,3번째 반복을 수행하면서 학습 폴드 데이터로 학습된 개별 모델이 원본 데이터셋으로 예측한 결괏값을 최종 평균하여 메타 모델에서 사용될 데이터를 만들게 된다.
STEP2

마지막 그림은 스텝1와 스텝2를 모두 포함한 CV 기반 스태킹 모델 전체를 도식화한 그림이다. 스텝 2는 각 모델들이 스텝1로 생성한 학습/테스트 데이터를 모두 합쳐, 최종적으로 메타 모델이 학습할 학습/테스트 데이터를 생성하기만 하면 된다.
최종 학습 데이터와 원본 데이터의 레이블 데이터를 합쳐서 메타 모델을 학습한 후, 최종 테스트 데이터로 예측을 수행한 뒤, 최종 예측 결과를 원본 테스트 데이터의 레이블 데이터와 비교해 평가 수행
위 설명을 코드로 구현해보자.
- 개별 모델이 메타 모델을 위한 학습용/테스트 데이터 생성
- get_stacking_base_datasets() 함수 생성, 이 함수에서
- 개별 모델의 classifier 객체
- 원본 학습용 피처 데이터
- 원본인 학습용 레이블 데이터
- 원본인 테스트 피처 데이터
- k fold를 몇 개로 할지
를 파라미터로 입력받는다.
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
# 개별 기반 모델에서 최종 메타 모델이 사용할 학습 및 테스트용 데이터를 생성하는 함수
def get_stacking_base_datasets(model, X_train_n, y_train_n, X_test_n, n_folds):
# 지정된 n_folds 값으로 KFold 생성
kf = KFold(n_splits=n_folds, shuffle=True, random_state=0)
# 추후에 메타 모델이 학습할 학습 데이터 반환을 위한 넘파이 배열 초기화
train_fold_pred = np.zeros((X_train_n.shape[0], 1))
test_pred = np.zeros((X_test_n.shape[0], n_folds))
print(model.__class__.__name__,'model 시작')
for folder_counter, (train_index, valid_index) in enumerate(kf.split(X_train_n)):
# 입력된 학습 데이터에서 기반 모델이 학습/예측할 폴드 데이터셋 추출
print('\t 폴드 세트:', folder_counter+1, '시작')
X_tr = X_train_n[train_index]
y_tr = y_train_n[train_index]
X_te = X_train_n[valid_index]
#폴드 세트 내부에서 다시 만들어진 학습 데이터로 기반 모델의 학습 수행
model.fit(X_tr, y_tr)
# 폴드 세트 내부에서 다시 만들어진 검증 데이터로 기반 모델 예측 후 데이터 저장
train_fold_pred[valid_index, :] = model.predict(X_te).reshape(-1,1)
# 입력된 원본 테스트 데이터를 폴드 세트 내 학습된 기반 모델에서 예측 후 데이터 저장
test_pred[:, folder_counter] = model.predict(X_test_n)
# 폴드 세트 내에서 원본 테스트 데이터를 예측한 데이터를 평균하여 테스트 데이터로 생성
test_pred_mean = np.mean(test_pred, axis=1).reshape(-1,1)
# train_fold_pred는 최종 메타 모델이 사용하는 학습 데이터, test_pred_mean은 테스트 데이터
return train_fold_pred, test_pred_meanknn_train, knn_test = get_stacking_base_datasets(knn_clf, X_train, y_train, X_test, 7)
rf_train, rf_test = get_stacking_base_datasets(rf_clf, X_train, y_train, X_test, 7)
dt_train, dt_test = get_stacking_base_datasets(dt_clf, X_train, y_train, X_test, 7)
ada_train, ada_test = get_stacking_base_datasets(ada_clf, X_train, y_train, X_test, 7)# STEP2
Stack_final_X_train = np.concatenate((knn_train, rf_train, dt_train, ada_train), axis=1)
Stack_final_X_test = np.concatenate((knn_test, rf_test, dt_test, ada_test), axis=1)
print('스태킹 학습 피처 데이터 Shape:' , Stack_final_X_train.shape,
'스태킹 테스트 히처 데이터 Shape:', Stack_final_X_test.shape)
# 4개의 개별 모델 예측값을 합친 것이므로 칼럼 크기는 4이다.[Out]
스태킹 학습 피처 데이터 Shape: (455, 4) 스태킹 테스트 히처 데이터 Shape: (114, 4)# 최종 메타 모델인 로지스틱 회귀를 스태킹된 학습용 피처 데이터셋과 원본 학습 레이블 데이터로
# 학습한 후에 스태킹된 테스트 데이터셋으로 예측하고, 예측 결과를 원본 테스트 레이블 데이터와
# 비교해 정확도를 예측해보자.
lr_final.fit(Stack_final_X_train,y_train)
stack_final = lr_final.predict(Stack_final_X_test)
print('최종 메타 모델의 예측 정확도: {0:.4f}'.format(accuracy_score(y_test, stack_final)))[Out]
최종 메타 모델의 예측 정확도: 0.9649-최종 메타 모델의 정확도는 96.49%로 측정되었다.
- 이 예제에서는 파라미터 튜닝을 최적으로 하지 않았지만, 일반적으로 스태킹을 이루는 모델은 최적으로 파라미터를 튜닝한 상태에서 스태킹 모델을 만드는 것이 일반적이다.
- 스태킹 모델의 파라미터 튜닝은 개별 알고리즘 모델의 파라미터를 최적으로 튜닝하는 것을 말한다.
- 스태킹 모델은 분류 뿐만 아니라, 회귀에도 적용가능하다.
4-11. 정리
1. 대부분의 앙상블 기법은 결정 트리 기반의 다수의 약한 학습기를 결합해 별동성을 줄여 예측 오류를 줄이고 성능을 개선한다.
2. 결정 트리 알고리즘은 "정보의 균일도"에 기반한 규칙 트리를 만들어서 예측을 수행, 단점은 균일한 최종 예측 결과를 도출하기 위해 결정 트리가 깊어지고 복잡해지면서 과적합이 쉽게 발생하는 것
3. 앙상블 기법은 대표적으로 배깅과 부스팅으로 구분
3-1. 배깅은 학습 데이터의 중복을 허용하면서 다수의 세트로 샘플링하여 다수의 약한 학습기가 학습 한뒤 최종 결과를 결합하여 예측하는 방식 (EX. 랜덤 포레스트)
3-2. 부스팅은 학습기들이 순차적으로 학습을 진행하면서 예측이 틀린 데이터에 대해서는 가중치를 부여해, 다음번 학습기가 학습할 때에는 이전에 예측이 틀린 데이터에 대해서 보다 높은 정확도로 예측할 수 있도록 함 (EX. XGBoost, LightGBM)
- LightGBM은 XGBoost보다 학습 수행 시간이 빠르다.
4. 마지막으로 스태킹 모델은 여러개의 개별 모델이 생성한 예측 데이터를 기반으로 최종 메타 모델이 학습할 별도의 학습 데이터셋과 예측할 데이터셋을 재 생성하는 기법




