| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 부트 스트래핑
- 데이터 핸들링
- lightgbm
- WITH ROLLUP
- 리프 중심 트리 분할
- 캐글 산탄데르 고객 만족 예측
- 그룹 연산
- Growth hacking
- XGBoost
- tableau
- DENSE_RANK()
- 데이터 정합성
- 그로스 해킹
- 데이터 증식
- python
- 분석 패널
- sql
- 캐글 신용카드 사기 검출
- ImageDateGenerator
- splitlines
- pmdarima
- 컨브넷
- WITH CUBE
- 그로스 마케팅
- ARIMA
- 마케팅 보다는 취준 강연 같다(?)
- 로그 변환
- 인프런
- 스태킹 앙상블
- 3기가 마지막이라니..!
- Today
- Total
LITTLE BY LITTLE
[7] 파이썬 머신러닝 완벽 가이드 - 4. 분류(결정 트리-제약을 통한 과적합 해결, 앙상블-보팅-소프트 보팅과 하드 보팅) 본문
[7] 파이썬 머신러닝 완벽 가이드 - 4. 분류(결정 트리-제약을 통한 과적합 해결, 앙상블-보팅-소프트 보팅과 하드 보팅)
위나 2022. 8. 15. 14:554. 분류
- 분류의 개요
- 결정 트리
- 앙상블 학습
- 랜덤 포레스트
- GBM(Gradient Boosting Machine)
- XGBoost(eXtra Gradient Boost)
- LightGBM
- 분류 실습 - 캐글 산탄데르 고객 만족 예측
- 분류 실습 - 캐글 신용카드 사기 검출
- 스태킹 앙상블
- 정리
- 회귀
- 회귀 소개
- 단순 선형 회귀를 통한 회귀 이해
- 비용 최소화하기 - 경사 하강법 (Gradient Descent) 소개
- 사이킷런 Linear Regression을 이용한 보스턴 주택 가격 예측
- 다항 회귀와 과(대)적합/과소적합 이해
- 규제 선형 모델 - 릿지, 라쏘, 엘라스틱 넷
- 로지스틱 회귀
- 회귀 트리
- 회귀 실습 - 자전거 대여 수요 예측
- 회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
- 정리
- 차원 축소
- 차원 축소의 개요
- PCA (Principal Component Anlysis)
- LDA (Linear Discriminant Anlysis)
- SVD (Singular Value Decomposition)
- NMF (Non-Negative Matrix Factorization)
- 정리
- 군집화
- K-평균 알고리즘 이해
- 군집 평가
- 평균 이동 (Mean shift)
- GMM(Gaussian Mixture Model)
- DBSCAN
- 군집화 실습 - 고객 세그먼테이션
- 정리
- 텍스트 분석
- 텍스트 분석 이해
- 텍스트 사전 준비 작업(텍스트 전처리) - 텍스트 정규화
- Bag of Words - BOW
- 텍스트 분류 실습 - 20 뉴스그룹 분류
- 감성 분석
- 토픽 모델링 - 20 뉴스그룹
- 문서 군집화 소개와 실습 (Opinion Review 데이터셋)
- 문서 유사도
- 한글 텍스트 처리 - 네이버 영화 평점 감성 분석
- 텍스트 분석 실습 - 캐글 mercari Price Suggestion Challenge
- 정리
- 추천 시스템
- 추천 시스템의 개요와 배경
- 콘텐츠 기반 필터링 추천 시스템
- 최근접 이웃 협업 필터링
- 잠재요인 협업 필터링
- 콘텐츠 기반 필터링 실습 - TMDV 5000 영화 데이터셋
- 아이템 기반 최근접 이웃 협업 필터링 실습
- 행렬 분해를 이용한 잠재요인 협업 필터링 실습
- 파이썬 추천 시스템 패키지 - Surprise
- 정리
4-1. 분류의 개요
- 명시적인 정답(레이블)이 있는 데이터가 주어진 상태에서 학습하는 지도학습의 대표적인 유형이다.
- 주어진 데이터의 피처와 레이블값을 머신러닝 알고리즘으로 학습해 모델을 생성하고, 이렇게 생성된 모델에 새로운 데이터 값이 주어졌을 때 미지의 레이블 값을 예측하는 것
- 기존 데이터가 어떤 레이블에 속하는지 패턴을 알고리즘으로 인지한 뒤, 새롭게 관측된 데이터에 대한 레이블 판별
- 분류를 위한 머신러닝 알고리즘 종류
- Naive Bayes
- Logistic Regression 독립변수와 종속변수의 선형 관계성에 기반
- Decesion Tree 데이터 균일도에 따른 규칙 기반
- Support Vector Machine 개별 클래스 간의 최대 분류 마진을 효과적으로 찾아줌
- Nearest Neighbor 근접 거리 기준 최소 근접 알고리즘
- Neural Network 심층 연결 기반 신경망
- Ensemble 서로 같은/다른 머신러닝 알고리즘 결합
- Bagging과 Boosting으로 나뉜다.
- Bagging의 대표는 Random Forest
- Boosting의 효시는 Gradient Boosting (-)시간 오래걸림 → XgBoost, Light GBM 등장 → 부스팅은 정형 데이터 분류 영역에서 가장 활용도가 높은 알고리즘으로 자리잡음
- 앙상블은 서로 같거나 다른 알고리즘을 결합하는 것인데, 대부분은 동일한 알고리즘을 결합한다.
- 앙상블의 기본 알고리즘으로 일반적으로 사용하는 것은 결정 트리이다.
- (+) 결정 트리는 매우 쉽고 유연하게 적용될 수 있다.
- (+) 또한 결정 트리는 데이터의 스케일링이나 정규화 등 사전 가공의 영향이 매우 적다.
- (-) 예측 성능을 향상시키기 위해 복잡한 규칙 구조를 가져야 한다.
- (-) 따라서 복잡한 규칙 구조 대문에, 과적합이 발생해 반대로 예측 성능이 저하될 수도 있다.
- 하지만 결정트리의 이러한 단점이 앙상블 기법에서는 오히려 장점으로 작용한다. 앙상블은 많은 여러개의 약한 학습기를 결합해, 확률적 보완과 오류가 발생한 부분에 대한 가중치를 계속 업데이트하면서 예측 성능을 향상시키는데, 결정 트리가 좋은 약한 학습기가 되기 때문이다.
- Bagging과 Boosting으로 나뉜다.
- 이미지, 영상, 음성, NLP 영역에서 신경망에 기반한 딥러닝이 머신러닝계를 선도하고 있지만, 이를 제외한 정형 데이터 예측 분석에서는 앙상블이 많이 쓰임
4-2. 결정 트리
- 데이터에 있는 규칙을 학습을 통해 자동으로 찾아내 트리 기반의 분류 규칙을 만든다.
- 일반적으로 규칙을 가장 쉽게 표현하는 방법은 if/else 기반으로 나타내는 것, 쉽게 말하면 스무고개처럼 룰 기반의 프로그램에 적용되는 if, else를 자동으로 찾아내 예측을 위한 규칙을 만드는 알고리즘
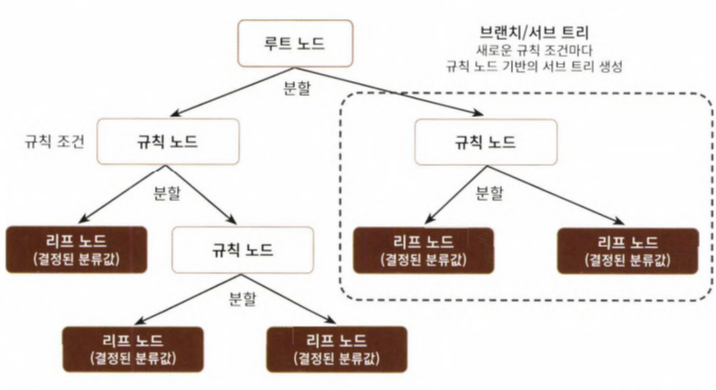
- 새로운 규칙 조건마다 서브 트리가 생성된다. 많은 규칙이 있을 수록 분류를 결정하는 방식이 복잡해진다는 의미이기에, 과적합으로 이어지기 쉽다. 트리의 깊이가 깊어질 수록 결정 트리의 예측 성능이 저하될 가능성이 높다.
- 적은 결정 노드로 높은 예측 정확도를 가지려면, 데이터를 분류할 때 최대한 많은 데이터셋이 해당 분류에 속할 수 있도록 결정노드의 규칙이 정해져야 한다. → 트리를 어떻게 분할할 것인가가 중요하고, 최대한 균일한 데이터셋을 구성할 수 있도록 분할해야 한다.

- 이러한 데이터 셋의 균일도는 데이터를 구분하는데 필요한 정보의 양에 영향을 미친다.
- A와 같이 균일도가 낮은 데이터셋에서는 검은 공을 예측하는데에 훨씬 더 많은 정보가 필요
- 결정 노드는 정보 균일도가 높은 데이터셋을 먼저 선택할 수 있도록 규칙 조건을 만든다. 균일도가 높은 자식 데이터셋을 쪼개는 방식을 자식 트리로 내려가며 반복하는 방식
- 정보 균일도를 측정하는 대표적인 방법은 '엔트로피를 이용한 정보 이득(Information Gain)지수와 지니계수가 있다.
-* 엔트로피 : 주어진 데이터 집합의 혼잡도, 서로 다른 값이 섞여있으면 엔트로피가 높은 것
-* 정보이득지수는 1에서 엔프로피 지수를 뺀 값, 결정트리는 이 정보 이득 지수로 분할 기준을 정한다. 정보 이득이 높은 속성을 기준으로 분할
- *지니 계수 : 지니계수는 경제학에서 불평등 지수를 나타낼 때 사용하는 계수로, 0이 가장 평등, 1로 갈수록 불평등. 머신러닝에 적용될 때에는 지니 계수가 낮을수록 데이터 균일도가 높음, 지니 계수가 낮은 속성을 기준으로 분할한다.
- DecisionTreeClassifier은 기본으로 지니계수를 이용해 데이터셋을 분할, 정보 이득이 높거나 지니 계수가 낮은 조건을 찾아서 자식 트리 노드에 걸쳐 반복적으로 분할한 뒤, 데이터가 모두 특정 분류에 속하게되면 분할을 멈추고 분류 결정
결정 트리 모델의 특징
- 결정트리의 가장 큰 장점은 ' 정보의 균일도 ' 라는 룰을 기반으로 하고 있어서 알고리즘이 쉽고 직관적
- 또 룰이 매우 명확하고, 어떻게 규칙노드/리프노드가 만들어지는지 이해가 쉽고, 시각화로 표현까지 가능
- 정보의 균일도만 신경쓰면 되므로, 특별한 경우를 제외하고는 피처의 스케일링, 정규화 작업과 같은 전처리 필요X
- 반면 가장 큰 단점은 '과적합'으로 정확도가 떨어지는 것
- 모든 데이터 상황을 만족하는 완벽한 규칙을 만들지 못하는 경우가 더 많음에도 불구하고, 정확도를 높이기 위해서 조건을 계속 추가하면서, 트리 깊이가 계속 커지고, 결과적으로 복잡한 학습 모델에 이르게 된다.
- 차라리 모든 데이터 상황을 만족하는 완벽한 규칙은 만들 수 없다고 먼저 인정하는 편이 더 나은 성능 보장 → 트리의 크기를 사전에 제한하는 것이 오히려 성능 튜닝에 더 도움이 된다.

결정 트리 파라미터
- DecisionTreeClassifier , DecisionTreeRegressor 클래스 제공
- 사이킷런의 결정 트리 구현은 CART알고리즘 기반이다. CART는 분류 뿐만 아니라, 회귀에서도 사용될 수 있는 트리 알고리즘


- min_samples_split 노트 분할을 위한 최소 샘플 데이터 수 (과적합 제어하는데 사용)
- min_samples_leaf 말단 노드가 되기 위한 최소한의 샘플 데이터 수 (마찬가지로 과적합 제어 용도이나, 비대칭적 데이터의 경우 특정 클래스의 데이터가 극도로 작을 수 있어 작게 설정할 필요가 있다.)
- max_features 최적 분할을 위해서 고려해야할 최대 피처 개수
- max_depth 트리의 최대 깊이를 규정
- max_leaf_nodes 말단 노드(Leaf)의 최대 개수
결정 트리 모델의 시각화 (실습 생략)
- Graphviz 패키지 이용(그래프 기반의 dot 파일로 기술된 다양한 이미지를 쉽게 시각화할 수 있는 패키지)
- 사이킷런의 export_graphviz() API : 함수 인자로 학습이 완료된 Estimator, 피처의 이름 리스트, 레이블 이름 리스트를 입력하면 학습된 결정 트리 규칙을 실제 트리 형태로 시각화해 보여준다.

- 1번 노드 = 루트 노드
- samples=120 : 전체 데이터가 120개
- value = [41, 40, 39] : Setosa 41개, Veriscolor 40개, Virginica 39개로 데이터 구성
- sample 120개가 value=[41,40,39] 분포도로 되어 있으므로 지니 계수는 0.667
- petal length(cm) ← 2.45 : 규칙으로 자식 노드 생성
- class = setosa : 하위 노드를 가질 경우, setosa의 개수가 41개로 제일 많다는 의미
- 2번 노드
- 위에서 petal_length(cm) ← 2.45 규칙이 True 또는 False로 분기하게 되면, 2번/3번 노드가 만들어진다.
- 2번 노드는 모든 데이터가 Setosa로 결정되므로, 클래스가 결정된 리프 노드가 되고, 더이상 2번 노드에서 규칙을 만들 필요가 없다.
- petal_length(cm) ← 2.45가 True인 규칙으로 생성되는 리프 노드
- value=[41,0,0], class=setosa : 41개의 샘플 데이터는 모두 Setosa이므로 예측 클래스는 Setosa로 결정
- 지니 계수는 0임
- 3번 노드
- Petal length(cm) ← 2.45 가 False인 규칙 노드
- 79개 샘플 데이터 중 Veriscolor 40개, Virginica 39개로 여전히 지니계수가 0.5로 높음(낮아져야 균일도↑)
- 다음 자식 브랜치 노드로 분기할 규칙 필요
- petal wiedth (cm) ← 1.55 규칙으로 자식 노드 생성
- 4번 노드
- value = [0,37,1] : Veriscolor 37개, Virginica가 1개로 대부분이 veriscolor
- 지니계수는 0.051로 매우 낮으나(균일도는 매우 높으나), 여전히 Veriscolor과 Virginica가 혼재되어 있으므로, petal length(cm) ← 5.25라는 새로운 규칙으로 다시 자식 노드 생성
- 5번 노드
- Petal width(cm) ← 1.55가 False인 규칙 노드
- value = [0,3, 38] : 41개의 샘플 데이터 중 Veriscolor 3개, Virginica 38개로 대부분이 Virginica
- 지니계수는 0.136으로 낮으나, 여전히 Veriscolor과 Virginica가 혼재되어 있으므로, petal width(cm) ← 1.75라는 새로운 규칙으로 다시 자식 노드 생성
- 각 노드의 색깔은 붓꽃 데이터의 레이블 값을 의미한다. 주황색은 0 Setosa, 초록색은 1 Veriscolor, 보라색은 2 Virginica, 색깔이 짙어질수록 지니 계수가 낮고(데이터 균일도가 높고), 해당 레이블에 속하는 샘플 데이터가 많다는 의미
- 4번 노드에서 38개중 37개가 같고 1개만 다른데에도 구분하기 위해서 다시 자식 노드를 생성한다. 이처럼 결정 트리는 규칙 생성 로직을 미리 제어하지 않으면 완벽하게 클래스 값을 구별해내기 위해 트리 노드를 계속해서 만들어간다.
- 파라미터로 알고리즘 제어 필요(max_depth)
- 자식 노드로 분할하기위한 최소한의 샘플 개수 설정(min_sample_splits) : 서로 다른 class값이 있어도 sample수가 n개 미만이면 split하지 않음
- 리프 노드가 될 수 있는 샘플 데이터 건수의 최솟값 지정 (min_samples_leaf)
- 리프 노드가 될 수 있는 조건은 디폴트로 1인데, min_samples_leaf=1의 의미는 단독 클래스이거나, 단 1개의 데이터로 되어있을 경우에는 리프 노드가 될 수 있음 (브랜치 노드↔리프 노드)
- min_samples_leaf = 4로 설정하면 샘플이 4 이하이면, 리프 노드가 되기 때문에 지니 계수값이 크더라도(균일도가 낮더라도), 샘플이 4인 조건으로 규칙 변경을 선호하게 되어, 자연스럽게 브랜치 노드가 줄어들고, 결정 트리가 더 간결하게 만들어진다.
- 중요한 몇개의 피처가 명확한 규칙 트리를 만드는데 크게 기여하여, 균일도에 기반해 어떤 속성을 규칙 조건으로 선택하느냐가 중요한 요건이다.모델이 간결하고 이상치에 강한 모델을 만들 수 있음
- 규칙을 정하는데 있어 피처의 중요한 역할 지표를 DecisionTreeClassifier의 객체 feature_importances 속성으로 제공
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# DecisionTree Classifier 생성
dt_clf = DecisionTreeClassifier(random_state=156)
# 붓꽃 데이터를 로딩하고, 학습과 테스트 데이터셋으로 분리
iris_data=load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target,
test_size=0.2, random_state=11)
# DecisionTreeClassifier 학습
dt_clf.fit(X_train, y_train)feature importance 예제
[In]
import seaborn as sns
import numpy as np
%matplotlib inline
# feature importance 추출
print("Feature importances:\n{0}".format(np.round(dt_clf.feature_importances_,3)))
# feature별 importance 매핑
for name, value, in zip(iris_data.feature_names, dt_clf.feature_importances_):
print('{0} : {1: .3f}'.format(name, value))[Out]
Feature importances:
[0.025 0. 0.555 0.42 ]
sepal length (cm) : 0.025
sepal width (cm) : 0.000
petal length (cm) : 0.555
petal width (cm) : 0.420
- 여러 피처 중 Petal_length가 가장 피처 중요도가 높음을 알 수 있다.
결정 트리 과적합(Overfitting)
- make_classification()함수로 분류를 위한 테스트용 데이터를 생성하자.
- make_classification(n_features, n_redundant, n_informative, n_classes, n_clusters_per_class, random_state)
- 이 함수를 이용해 2개의 피처가 3가지 유형의 클래스 값을 가지는 데이터셋을 만들고, 이를 그래프 형태로 시각화하자. make_classification() 호출 시 반환되는 객체는 피처 데이터 셋과 클래스 레이블 데이터셋
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
%matplotlib inline
plt.title("3 Class values with 2 Features Sample data creation")
# 2차원 시각화를 위해 피처는 2개, 클래스는 3가지 유형의 분류 샘플 데이터 생성
X_features, y_labels = make_classification(n_features=2, n_redundant=0,
n_informative=2, n_classes=3, n_clusters_per_class=1,
random_state=0)
# 그래프 형태로 2개의 피처로 2차원 좌표 시각화, 각 클래스 값은 다른 색깔로 표시됨
plt.scatter(X_features[:, 0], X_features[:, 1], marker='o', c=y_labels, s=25, edgecolor='k')
- 각 피처가 X,Y축으로 나열된 2차원 그래프이며, 3개의 클래스 값 구분은 색깔로 되어 있다.
- 이제 X_features와 y_labels 데이터 셋을 기반으로 결정 트리를 학습하자. 1번째 학습시에는 결정 트리 생성에 별다른 제약이 없도록 결정 트리의 하이퍼 파라미터를 디폴트로 한 뒤, 결정 트리 모델이 어떤 결정기준을 가지고 분할하는지, 데이터를 분류하는지 확인
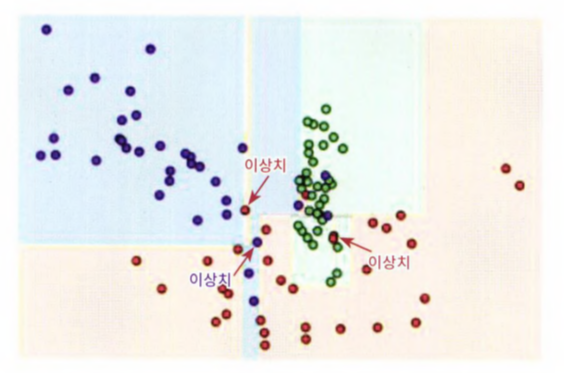
- 일부 이상치 데이터까지 분류하기 위해 분할이 자주 일어나서, 결정 기준 경계가 매우 많아졌다.
- 결정 트리의 기본 하이퍼 파라미터 설정은 리프 노드 안에 데이터가 모두 균일하거나 하나만 존재해야 하는 엄격한 분할 기준으로 인해 결정 기준 경계가 많아지고 복잡해졌다.
- 복잡한 모델은 데이터셋의 특성과 약간만 다른 형태의 데이터셋을 예측하면 예측 정확도가 떨어지게 된다.
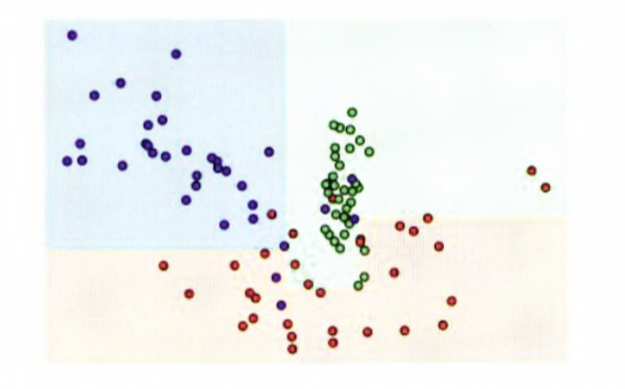
- min_sample_leaf=6을 설정하여, 6개 이하의 데이터는 리프 노드를 생성할 수 있도록 리프 노드 생성 규칙이 완화되었다.
- 이상치에 크게 반응하지 않으면 좀 더 일반화된 분류 규칙에 따라 분류됐음을 알 수 있다.
결정 트리 실습 - 사용자 행동 인식 데이터 셋
- 30명에게 스마트폰 센서를 장착한 뒤, 사람의 동작과 관련된 여러가지 피처를 수집한 데이터이다.
[In]
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
# features.txt 파일에는 피처 이름 index와 피처명이 공백으로 분리되어 있음.
feature_name_df = pd.read_csv('/features.txt',sep='\s+',
header=None, names=['column_index', 'column_name'])
feature_name_df.head()[Out]
column_index column_name
0 1 tBodyAcc-mean()-X
1 2 tBodyAcc-mean()-Y
2 3 tBodyAcc-mean()-Z
3 4 tBodyAcc-std()-X
4 5 tBodyAcc-std()-Y# 피처명 index를 제거하고, 피처명만 리스트 객체로 생성한 뒤 샘플로 10개만 추출
feature_name = feature_name_df.iloc[:, 1].values.tolist()
print('전체 피처명에서 10개만 추출:', feature_name[:10])전체 피처명에서 10개만 추출: ['tBodyAcc-mean()-X', 'tBodyAcc-mean()-Y', 'tBodyAcc-mean()-Z', 'tBodyAcc-std()-X', 'tBodyAcc-std()-Y', 'tBodyAcc-std()-Z', 'tBodyAcc-mad()-X', 'tBodyAcc-mad()-Y', 'tBodyAcc-mad()-Z', 'tBodyAcc-max()-X']- 피처명을 보면 인체의 움직임과 관련된 속성의 평균/표준편차가 X,Y,Z축 값으로 되어있음에 유추할 수 있다.
- 피처명을 가지는 Dataframe을 이용해 데이터 파일을 데이터셋 Dataframe에 로딩하기 전 유의해야할 부분이 있다. - 중복된 피처명을 가지고 있어, 원본 피처명에 _1 또는 _2를 추가 부여해서 변경한 뒤에 이를 이용해서 데이터를 df에 로드
feature_dup_df = feature_name_df.groupby('column_name').count()
print(feature_dup_df[feature_dup_df['column_index']>1].count())
feature_dup_df[feature_dup_df['column_index']>1].head()column_index 42
dtype: int64
column_index
column_name
fBodyAcc-bandsEnergy()-1,16 3
fBodyAcc-bandsEnergy()-1,24 3
fBodyAcc-bandsEnergy()-1,8 3
fBodyAcc-bandsEnergy()-17,24 3
fBodyAcc-bandsEnergy()-17,32 3- 중복된 피처명만을 담은 ('column_index'>1) feature_dup_df를 생성해서 count한 결과, 42개의 피처명이 중복되어있다.
- 중복된 피처명에 대해 _1 또는 _2를 추가로 부여하는 함수 get_net_feature_name_df() 생성
def get_new_feature_name_df(old_feature_name_df):
feature_dup_df = pd.DataFrame(data=old_feature_name_df.groupby('column_name').
cumcount(), columns=['dup_cnt'])
feature_dup_df = feature_dup_df.reset_index()
new_feature_name_df = pd.merge(old_feature_name_df.reset_index(),
feature_dup_df, how='outer')
new_feature_name_df['column_name'] = new_feature_name_df[['column_name', 'dup_cnt']].apply(lambda x : x[0] +'_'+str(x[1])
if x[1] >0 else x[0], axis=1)
new_feature_name_df = new_feature_name_df.drop(['index'],axis=1)
return new_feature_name_df[In]
# 학습용 피처 데이터셋과 테스트용 피처 데이터셋 로드
# 레이블의 칼럼을 'action'으로
import pandas as pd
def get_human_dataset():
# 공백 분리 파일 => read_csv에서 공백문자를 sep으로 할당
feature_name_df = pd.read_csv('/features.txt', sep='\s+', header=None, names=
['column_index', 'column_name'])
# 앞서 만든 함수로 신규 피처명 df 생성
new_feature_name_df = get_new_feature_name_df(feature_name_df)
# df에 피처명을 칼럼으로 부여하기위해 리스트 객체로 다시 변환
feature_name = new_feature_name_df.iloc[:, 1].values.tolist()
# 학습 피처 데이터셋과 테스트 피터 데이터를 df로 로딩, 칼럼명은 feature_name
X_train = pd.read_csv('/X_train.txt', sep='\s+', names=feature_name)
X_test = pd.read_csv('/X_test.txt', sep='\s+', names=feature_name)
# 학습 레이블과 레이블 데이터를 df로 로딩하고, 칼럼명은 action으로 부여
y_train = pd.read_csv('/y_train.txt', sep='\s+', header=None, names=['action'])
y_test = pd.read_csv('/y_test.txt', sep='\s+', header=None, names=['action'])
# 로드된 학습/테스트용 df 모두 반환
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = get_human_dataset()
print('## 학습 피처 데이터셋 info()')
print(X_train.info())[Out]
## 학습 피처 데이터셋 info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 7352 entries, 0 to 7351
Columns: 561 entries, tBodyAcc-mean()-X to angle(Z,gravityMean)
dtypes: float64(561)
memory usage: 31.5 MB
None- 7352개의 레코드로 561개의 피처를 가지고 있다. 전부 float 숫자형이라서 별도의 카테고리 인코딩은 수행할 필요가 없다.
[In]
print(y_train['action'].value_counts())[Out]
6 1407
5 1374
4 1286
1 1226
2 1073
3 986
Name: action, dtype: int64- 특정 값으로 왜곡되지 않고, 비교적 고르게 분포되어있다.
[In]
# DecisionTreeClassifier로 동작 예측 분류를 수행해보자.
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
# 예제 반복시마다 동일한 예측 결과 도출을 위해 random_state 설정
dt_clf = DecisionTreeClassifier(random_state=156)
dt_clf.fit(X_train, y_train)
pred = dt_clf.predict(X_test)
accuracy = accuracy_score(y_test, pred)
print('결정 트리 예측 정확도: {0: .4f}'.format(accuracy))[Out]
결정 트리 예측 정확도: 0.8548[In]
# DecisionTreeClassifier의 하이퍼 파라미터 추출
print('DecisionTreeClassifier 기본 하이퍼 파라미터:\n', dt_clf.get_params())[Out]
DecisionTreeClassifier 기본 하이퍼 파라미터:
{'ccp_alpha': 0.0, 'class_weight': None, 'criterion': 'gini', 'max_depth': None, 'max_features': None, 'max_leaf_nodes': None, 'min_impurity_decrease': 0.0, 'min_samples_leaf': 1, 'min_samples_split': 2, 'min_weight_fraction_leaf': 0.0, 'random_state': 156, 'splitter': 'best'}- 이번에는 결정 트리의 트리 깊이가 예측 정확도에 주는 영향을 살펴보자. 결정 트리의 경우, 분류를 위해 리프 노드(=클래스 결정 노드)가 될 수 있는 적합한 수준이 될 때까지 지속해서 트리의 분할을 수행하면서 깊이가 깊어진다.
- GridSearchCV를 이용해서 결정 트리의 깊이를 조절할 수 있는 하이퍼 파라미터인 max_depth값을 변화시키면서 예측성능을 확인해보자.
# GridSearchCV
from sklearn.model_selection import GridSearchCV
params = {'max_depth' : [6, 8, 10, 12, 16, 20, 24]}
grid_cv = GridSearchCV(dt_clf, param_grid=params, scoring='accuracy', cv=5, verbose=1)
grid_cv.fit(X_train,y_train)
print('GridSerachCV 최고 평균 정확도 수치: {0:.4f}'.format(grid_cv.best_params_))
print('GridSerachCV 최적 하이퍼 파라미너:', grid_cv.best_params_)- max_depth가 8일 때, 5개의 폴드 세트의 최고 평균 정확도 결과가 약 85.26%이다.
- 과정을 GridSerachCV 객체의 cv_result_ 속성을 통해 자세히 살펴보자.
[In]
# GridSearchCV
from sklearn.model_selection import GridSearchCV
params = {'max_depth' : [6, 8, 10, 12, 16, 20, 24]}
grid_cv = GridSearchCV(dt_clf, param_grid=params, scoring='accuracy', cv=5, verbose=1)
grid_cv.fit(X_train,y_train)
print('GridSerachCV 최고 평균 정확도 수치: {0:.4f}'.format(grid_cv.best_score_))
print('GridSerachCV 최적 하이퍼 파라미터:', grid_cv.best_params_)[Out]
GridSearchCV 최고 평균 정확도 수 치: 0.8526
GridSearchCV 최적 하이퍼 파라미터: {'max.depth':8}- max_depth가 8일 때 5개 폴드 세트의 최고 평균 정확도 결과가 약 85.26%로 도출되었다.
- max_depth를 증가시켜 예측 성능의 변화를 확인해보자. GridSearchCV 객체의 cv_results_ 속성은 CV세트에 하이퍼 파라미터를 순차적으로 입력했을 때의 성능 수치를 갖고있다.
[In]
# GridSearchCV 객체의 cv_results_ 속성을 DataFrame으로 생성 .
cv_results_df = pd.DataFrame(grid_cv.cv_results_)# max_depth 파라미터 값과 그 때의 테스트 셋, 학습 데이터셋의 정확도 수치 추출
cv_results_df[['param_max_depth', 'mean_test_score']][Out]
param_max_depth mean_test_score
0 6 0.850925
1 8 0.852557
2 10 0850925
3 12 0.844124
4 16 0852149
5 20 0851605
6 24 0.850245- max_depth가 8일 때 mean_test_score이 0.852로 정확도가 정점이다. 이를 넘어가면서 정확도가 계속 떨어짐
- 깊어진 트리는 학습 데이터셋에서는 올바른 예측 결과를 가져올지 몰라도, 검증 데이터셋에서는 오히려 과적합으로 인한 - 성능 저하를 유발하게됨을 보여준다.
- 이번에는 테스트 데이터셋에서 결정트리의 정확도를 측정해보자.
[In]
#테스트 데이터셋에서 max_depth변화에 따른 측정
max_depth = [6, 8, 10, 12, 16, 20, 24]
# max_depth 값을 변화시키면서 그 때마다 학습과 테스트셋에서의 예측 성능 측정
for depth in max_depth:
dt_clf = DecisionTreeClassifier(max_depth=depth, random_state=156)
dt_clf.fit(X_train, y_train)
pred = dt_clf.predict(X_test)
accuracy = accuracy_score(y_test, pred)
print('max_depth = {0} 정확도: {1:.4f}'.format(depth, accuracy))[Out]
max.depth = 6 정확도: 0.8558
max_depth = 8 정확도: 0.8707
max_depth = 10 정확도: 0.8673
max_depth = 12 정확도: 0.8646
max_depth = 16 정확도: 0.8575
max_depth = 20 정확도: 0.8548
max_depth = 24 정확도: 0.8548- max_depth가 8일 때 가장 높은 정확도 87.07%를 보임, 8을 넘어가면서 정확도 감소
- 앞의 GirdSearchCV 예제와 마찬가지로, 깊이가 깊어질 수록 테스트 데이터셋의 정확도는 더 떨어진다.
- 복잡한 모델보다도 트리의 깊이를 낮춘 단순한 모델이 더욱 효과적인 결과를 가져올 수 있음
- max_depth와 min_samples_spilt을 같이 변경하면서 정확도 성능을 튜닝해보자.
[In]
params = {'max_depth' : [8, 12, 16, 20], 'min_samples_split' : [16, 24],}
grid_cv = GridSearchCV(dt_clf, param_grid=params, scoring='accuracy', cv=5, verbose=1)
grid_cv.fit(X_train, y_train)
print('GridSearchCV 최고 평균 정확도 수치: {0:.4f}'.format(grid_cv.best_score_))
print('GridSearchCV 최적 하이퍼 파라미터:', grid_cv.best params_)[Out]
GridSearchCV 최고 평균 정확도 수 치: 0.8550
GridSearchCV 최적 하이퍼 파라미터: {'max_depth' :8, 'min_samples_split1:16}위의 최적의 하라미터를 이용해 테스트 데이터셋에 예측을 수행해보자.
[In]
best_df_clf = grid_cv.best_estimator_
pred1 = best_df_clf.predict(X_test)
accuracy = accuracy_score(y_test, pred1)
print('결정 트리 예측 정확도:{0:.4f}'.format(accuracy))[Out]
결정 트리 예측 정확도:0.8717마지막으로 각 피처의 중요도를 feature_importances_ 속성을 이용해 알아보자. 중요도가 높은 순으로 Top20 피처를 막대그래프로 표현
# 피처의 중요도 시각화
import seaborn as sns
ftr_importances_values = best_df_clf.feature_importances_
# top 중요도로 정렬을 쉽게, seaborn 막대그래프로 쉽게 표현하기 위해 series 변환
ftr_importances = pd.Series(ftr_importances_values, index=X_train.columns)
# 중요도 순 정렬
ftr_top20 = ftr_importances.sort_values(ascending=False)[:20]
plt.figure(figsize=(8,6))
plt.title('Feature importances Top 20')
sns.barplot(x=ftr_top20, y= ftr_top20.index)
plt.show()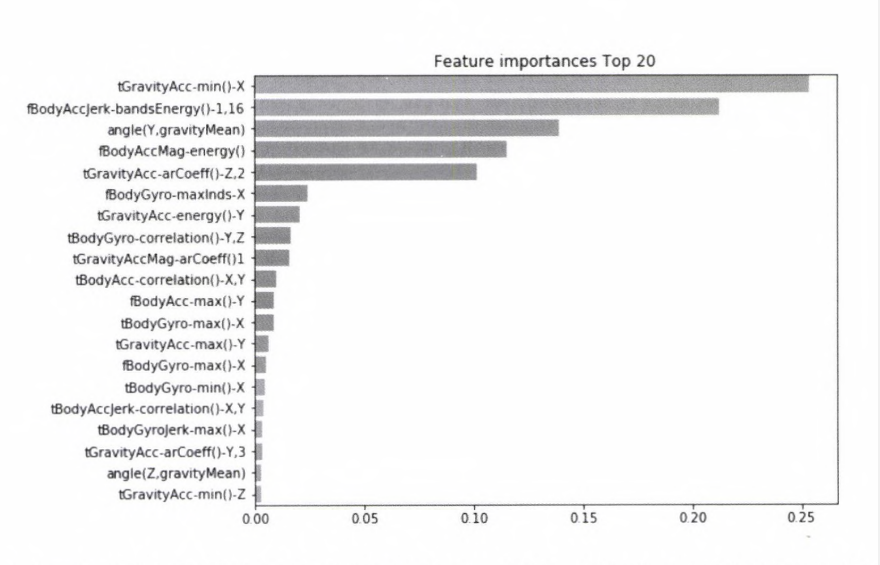
4-3. 앙상블 학습
- 앙상블 학습은 여러개의 분류기(classifier)를 생성하고, 그 예측을 결합함으로써 정확한 최종 예측을 도출하는 기법
- 정형 데이터 분류시 앙상블이 뛰어난 성능을 보이고 있다.
- 대표적으로 랜덤 포레스트, 그래디언트 부스팅 알고리즘이 있다.
- 앙상블 학습의 유형은 보팅, 배깅, 부스팅 3가지로 나눌 수 있다.
- 보팅(voting)의 경우 서로 다른 알고리즘 결합
- 배깅(bagging)의 경우 분류기가 모두 같은 유형의 알고리즘 기반이지만, 데이터 샘플링을 서로 다르게 가져가면서 학습을 수행해 보팅(voting)을 수행하는 것 (대표적인 배깅 방식 - 랜덤 포레스트)
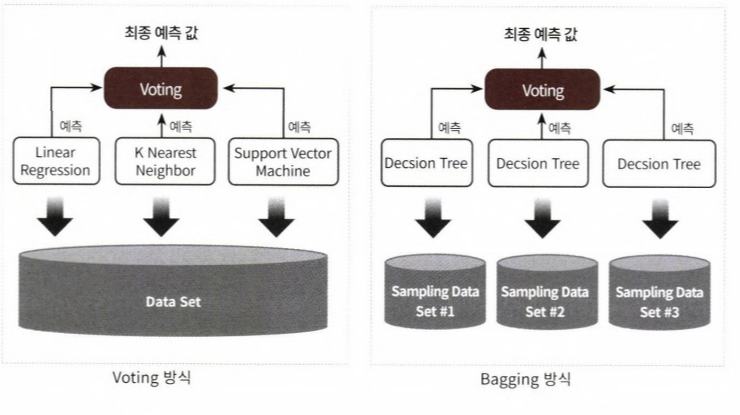
- 왼쪽 그림을 보팅 분류기를 도식화한 것이다. 선형 회귀, k최근접 이웃, 서포트 벡터 머신 3가지 ml알고리즘이 같은 데이터셋에 대해 학습,예측한 결과로 보팅을 통해 최종 예측 결과 선정
- 오른쪽 그림은 배깅 분류기를 도식화한 것이다. 단일 ml알고리즘(결정트리)으로 여러 분류기가 학습으로 개별 예측을 하는데, 학습하는 데이터셋이 보팅 방식과는 다르다.
- 개별 분류기에 할당된 학습 데이터는 원본 학습 데이터를 샘플링해 추출하는데, 이렇게 개별 classifier에게 데이터를 샘플링해서 추출하는 방식을 boostrapping (부트 스트래핑 분할 방식)이라 부른다.
- 개별 분류기가 부트 스트래핑 방식으로 샘플링된 데이터 세트에 대해서 학습을 통해 개별적인 예측을 수행한 결과를 보팅 을 통해서 최종 예측 결과를 선정하는 방식이 배깅 앙상블 방식이다.
- 교차 검증이 데이터 세트 간에 중첩을 허용하지 않는 것과 다르게 배깅 방식은 중첩을 허용한다. 따라서 10000개의 데이터를 10개의 분류기가 배깅 방식으로 나누더라도 각 1000개의 데이터 내에는 중복된 데이터가 있다.
- 부스팅은 분류기들이 순차적으로 학습을 수행하는데, 앞서 수행한 분류기에서 틀린 예측이 올바르게 될 수 있도록 다음 분류기에 가중치를 부여하며 학습,예측 진행
- ex. Gradient Boost, XGBoost, LightGBM
보팅 유형 - 하드 보팅(Hard Voting)과 소프트 보팅(Soft Voting)
- 하드 보팅을 이용한 분류
- '다수결 원칙'과 비슷하다.
- 예측한 결과 중 다수의 분류기가 결정한 것을 최종 보팅 결괏값으로 선정
- 소프트 보팅을 이용한 분류 (일반적)
- 레이블 값 결정 확률을 모두 더하고, 이를 평균해서 가장 확률이 높은 레이블 값을 최종 보팅 결괏값으로 선정

보팅 분류기(Voting Classifier)
- VotingClassifier 클래스 제공
- 보팅 방식의 앙상블을 이용해 위스콘신 유방암 데이터셋을 예측 분석 해보자.
- 유방암의 악성 종양, 양성 종양 여부를 결정하는 이진 분류 데이터셋
- 종양의 크기, 모양 등 형태 관련 많은 피처
- load_brease_cancer() 함수로 데이터셋 생성
- 로지스틱 회귀와 KNN 기반으로 보팅 분류기를 만들어보자.
[In]
import pandas as pd
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_scorecancer = load_breast_cancer()
data_df = pd.DataFrame(cancer. data, columns=cancer.feature_names)
data_df.head(3)[Out]



[In]
# VotingClassifier로 보팅 분류기 생성 (로지스틱 회귀와 KNN 기반)
# 개별 모델은 로지스틱 회귀와 KNN
lr_clf = LogisticRegression()
knn_clf = KNeighborsClassifier(n_neighbors=8)
# 개별 모델을 소프트 보팅 기반의 앙상블 모델로 구현한 분류기
vo_clf = VotingClassifier( estimators = [('LR', lr_clf), ('KNN', knn_clf)], voting='soft')
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, test_size=0.2,
random_state=156)
# VotingClassifier 학습-예측-평가
vo_clf.fit(X_train, y_train)
pred = vo_clf.predict(X_test)
print('Voting 분류기 정확도: {0:.4f}'.format(accuracy_score(y_test,pred)))
# 개별 모델의 학습-예측-평가
classifiers = [lr_clf, knn_clf]
for classifier in classifiers:
classifier.fit(X_train, y_train)
pred = classifier.predict(X_test)
class_name = classifier.__class__.__name__
print('{0} 정확도: {1:.4f}'.format(class_name, accuracy_score(y_test, pred)))[Out]
Voting 분류기 정확도: 0.9474
LogisticRegression 정확도: 0.9386
KNeighborsClassifier 정확도: 0.9386- 편향- 분산 트레이드오프는 ML모델이 극복해야할 중요 과제
- 보팅,스태킹 등은 서로 다른 알고리즘을 기반으로 하고 있지만, 배깅,부스팅은 대부분 결정 트리 알고리즘을 기반으로 한다.
- 결정 트리 알고리즘은 쉽고 직관적인 분류 기준을 갖고 있지만, 정확한 예측을 위해 학습 데이터의 예외 상황에 집착한 나머지 오히려 과적합이 발생할 수 있다.
- 하지만, 앙상블 학습에서는 이 결정 트리 알고리즘의 단점을 수십,수천개의 매우 많은 분류기 결합을 통해 극복
- 결정 트리 알고리즘의 장점은 그대로 취하고, 단점은 보완하며 편향-분산 트레이드오프의 효과를 극대화할 수 있다.




