| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 캐글 신용카드 사기 검출
- WITH CUBE
- 리프 중심 트리 분할
- pmdarima
- 데이터 핸들링
- splitlines
- ARIMA
- 스태킹 앙상블
- python
- WITH ROLLUP
- 그룹 연산
- 로그 변환
- 마케팅 보다는 취준 강연 같다(?)
- 컨브넷
- 데이터 증식
- sql
- lightgbm
- 그로스 마케팅
- 캐글 산탄데르 고객 만족 예측
- tableau
- Growth hacking
- ImageDateGenerator
- 그로스 해킹
- 3기가 마지막이라니..!
- DENSE_RANK()
- 부트 스트래핑
- 데이터 정합성
- XGBoost
- 분석 패널
- 인프런
- Today
- Total
LITTLE BY LITTLE
[6] 파이썬 머신러닝 완벽 가이드 - 3.평가(정확도, 오차행렬, 정밀도, ROC AUC..) 본문
3. 평가
- 정확도
- 오차 행렬
- 정밀도와 재현율
- F1스코어
- ROC 곡선과 AUC
- 피마 인디언 당뇨병 예측
- 정리
- 분류
- 분류의 개요
- 결정 트리
- 앙상블 학습
- 랜덤 포레스트
- GBM(Gradient Boosting Machine)
- XGBoost(eXtra Gradient Boost)
- LightGBM
- 분류 실습 - 캐글 산탄데르 고객 만족 예측
- 분류 실습 - 캐글 신용카드 사기 검출
- 스태킹 앙상블
- 정리
- 회귀
- 회귀 소개
- 단순 선형 회귀를 통한 회귀 이해
- 비용 최소화하기 - 경사 하강법 (Gradient Descent) 소개
- 사이킷런 Linear Regression을 이용한 보스턴 주택 가격 예측
- 다항 회귀와 과(대)적합/과소적합 이해
- 규제 선형 모델 - 릿지, 라쏘, 엘라스틱 넷
- 로지스틱 회귀
- 회귀 트리
- 회귀 실습 - 자전거 대여 수요 예측
- 회귀 실습 - 캐글 주택 가격 : 고급 회귀 기법
- 정리
- 차원 축소
- 차원 축소의 개요
- PCA (Principal Component Anlysis)
- LDA (Linear Discriminant Anlysis)
- SVD (Singular Value Decomposition)
- NMF (Non-Negative Matrix Factorization)
- 정리
- 군집화
- K-평균 알고리즘 이해
- 군집 평가
- 평균 이동 (Mean shift)
- GMM(Gaussian Mixture Model)
- DBSCAN
- 군집화 실습 - 고객 세그먼테이션
- 정리
- 텍스트 분석
- 텍스트 분석 이해
- 텍스트 사전 준비 작업(텍스트 전처리) - 텍스트 정규화
- Bag of Words - BOW
- 텍스트 분류 실습 - 20 뉴스그룹 분류
- 감성 분석
- 토픽 모델링 - 20 뉴스그룹
- 문서 군집화 소개와 실습 (Opinion Review 데이터셋)
- 문서 유사도
- 한글 텍스트 처리 - 네이버 영화 평점 감성 분석
- 텍스트 분석 실습 - 캐글 mercari Price Suggestion Challenge
- 정리
- 추천 시스템
- 추천 시스템의 개요와 배경
- 콘텐츠 기반 필터링 추천 시스템
- 최근접 이웃 협업 필터링
- 잠재요인 협업 필터링
- 콘텐츠 기반 필터링 실습 - TMDV 5000 영화 데이터셋
- 아이템 기반 최근접 이웃 협업 필터링 실습
- 행렬 분해를 이용한 잠재요인 협업 필터링 실습
- 파이썬 추천 시스템 패키지 - Surprise
- 정리
3- 1. 정확도
- 예측 결과가 동일한 데이터 건수 / 전체 예측 데이터 건수
- 이진 분류의 경우, 데이터의 구성에 따라 ML모델의 성능을 왜곡할 수 있기 때문에 정확도 수치 하나만 가지고 성능을 평가하지 않는다.
- 다음 예제는 사이킷런의 BaseEstimator 클래스를 상속받아 아무런 학습을 하지 않고, 성별에 따라 생존자를 예측하는 단순한 Classifier를 생성한다. 사이킷런은 BaseEstimator을 상속받으면 Customized된 형태의 Estimator 생성 가능
- 생성할 MyDummyClssifier 클래스는 학습을 수행하는 fit() 메소드는 아무것도 수행하지 않으며 예측을 수행하는 predict() 메소드는 단순히 Sex 피처가 1이면 0, 그렇지 않으면 1로 예측하는 매우 단순한 Classifier이다.
지난번 타이타닉 예제 과정
[In]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
import sklearn
titanic_df=pd.read_csv('train.csv')
# 단순한 Classifier을 생성해보자.
from sklearn.base import BaseEstimator
class MyDummyClassifier(BaseEstimator):
def fit(self, X , y=None): # fit 메소드는 아무것도 학습하지 않음
pass
def predict(self, X): # predict 메소드는 단순히 Sex피처가 1이면 0, 그렇지않으면 1로 예측
pred = np.zeros( (X.shape[0], 1))
for i in range (X.shape[0]) :
if X['Sex'].iloc[i] ==1:
pred[i]=0
else:
pred[i]=1
return predfrom sklearn.preprocessing import LabelEncoder
# Null처리 함수 fillna
def fillna(df):
df['Age'].fillna(df['Age'].mean(), inplace=True)
df['Cabin'].fillna('N', inplace=True)
df['Fare'].fillna(0,inplace=True)
return df
# 머신러닝 알고리짐에 불필요한 속성 제거 함수 drop_features
def drop_features(df):
df.drop(['PassengerId','Name','Ticket'],axis=1, inplace=True)
return df
# 레이블 인코딩 함수 format_features
def format_features(df):
df['Cabin'] = df['Cabin'].str[:1]
features = ['Cabin', 'Sex', 'Embarked']
for feature in features:
le = LabelEncoder()
le = le.fit(df[feature])
df[feature] = le.transform(df[feature])
return df
# 모든 함수 호출 함수 transform_features(df):
def transform_features(df):
df = fillna(df)
df = drop_features(df)
df = format_features(df)
return df만들었던 전처리 함수를 이용해서, 바로 예측
# 생성된 MyDummyClassifier을 이용해 타이타닉 생존자 예측을 수행하고, 평가해보자.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# 원본 데이터 재로딩, 데이터 가공, 학습 데이터/테스트 데이터 분할
titanic_df = pd.read_csv('train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df = titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, test_size=0.2, random_state=0)# 위에서 생성한 Dummy Classifier를 이용해 학습/예측/평가 수행
myclf = MyDummyClassifier()
myclf.fit(X_train,y_train)
mypredictions = myclf.predict(X_test)
print('Dummy Classifier의 정확도 : {0:.4f}',format(accuracy_score(y_test,mypredictions)))[Out]
Dummy Classifier의 정확도 : {0:.4f} 0.7877094972067039- 단순한 알고리즘으로 예측했는데에도 불구하고, 정확도가 78.77%나 나왔다. 따라서 정확도는 적합한 평가지표가 아닌 것
- 타이타닉 데이터는 불균형한 레이블 값 분포를 갖고있어서, 정확도보다는 다른 지표가 더 적합
- 예를 들어 100개 데이터 중 90개 데이터 레이블이 0, 단 10개의 데이터 레이블이 1이라고 한다면 무조건 0으로 예측 결과를 반환하는 ML모델의 경우라도 정확도가 90%가 된다.

- 위의 MNIST 데이터셋을 변환해 불균형한 데이터셋으로 만들고, 정확도 지표 적용시 무슨 문제가 일어나는지 알아보자.
- 레이블 값이 7인 것만 True, 나머지는 모두 False로 변환해 이진 분류 문제로 바꾸자. (전체 데이터의 10%만 True, 나머지는 90%로 불균형한 데이터로 변형)
[In]
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.base import BaseEstimator
from sklearn.metrics import accuracy_score
import numpy as np
import pandas as pdclass MyFakeClassifier(BaseEstimator):
def fit( self, X, y):
pass
def predict ( self, X): # 입력되는 X데이터셋 크기만큼 모두 0값으로 만들어서 반환
return np.zeros( (len(X),1), dtype=bool)# 사이킷런의 내장 데이터 셋 load_digits()로 MNIST 데이터 로딩
digits = load_digits()# digits 번호가 7번이면 True이고, 이를 astype(int)로 1로 변환,
# 7번이 아니면 False이고, 0으로 변환
y = (digits.target == 7).astype(int)
X_train , X_test, y_train, y_test = train_test_split( digits.data, y, random_state=11)# 불균형한 레이블 데이터 분포도 확인
print('레이블 데이터 세트 크기:', y_test.shape)
print('테스트 세트 레이블 0과 1의 분포도')
print(pd.Series(y_test).value_counts())[Out]
레이블 데이터 세트 크기: (450,)
테스트 세트 레이블 0과 1의 분포도
0 405
1 45
dtype: int64# Dummy Classifier로 학습-예측-정확도 평가
fakeclf = MyFakeClassifier()
fakeclf.fit(X_train, y_train)
fakepred = fakeclf.predict(X_test)
print('모든 예측을 0으로 하여도 정확도는{:.3f}'.format(accuracy_score(y_test, fakepred)))[Out]
모든 예측을 0으로 하여도 정확도는0.900→ 정확도 평가 지표는 불균형한 레이블 데이터셋에서는 성능수치로 사용해서는 안된다. 이 한계를 극복하기 위한 다른 분류지표에 대해서 알아보자.
3-2. 오차 행렬
- 오차 행렬은 이진 분류에서 성능 지표로 잘 활용되며, 학습된 분류 모델이 예측을 수행하면서 얼마나 헷갈리고 있는지도 함께 보여준다.
- 즉, 이진 분류의 예측 오류가 얼마인지와 더불어, 어떠한 유형의 예측 오류가 발생하고 있는지 알 수 있다.

- TN : True Negative - 부정으로 예측했고, 맞음
- FP : False Positive - 긍정으로 예측했고, 틀림
- TP : True Positive - 긍정으로 예측했고, 맞음
- FN : False Negative - 부정으로 예측했고, 틀림
- 시계 방향으로 TN →FP→TP→FN
[In]
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, fakepred)사이킷런은 confusion_matrix API를 제공한다.
fakepred는 target이 7인지 아닌지 분류하는 이진 분류 데이터셋에서 무조건 Negative로 예측하는 Classifier이었다.
그리고 test data set 클래스 값의 분포는 0이 405건, 1이 45건이었다.
[Out]
# output
array([[405, 0],
[45, 0]], dtype=int64)- 출력된 오차 행렬은 ndarray형태이다. 상단의 도표와 같은 위치에 각각 TN, FP, FN, TP 수가 나타난다.
- 즉 TN은 405, FP는 0, TP는 0, FN은 45이다. → 0으로 예측해서 맞은건 405개, 0으로 예측해서 틀린건 45개.
- 이 4가지 값을 조합해서 정확도, 정밀도, 재현율 값을 알 수 있음
- 정확도는 "예측이 맞았는지"여부만 보여줌 True로 시작되는 TN과 TP의 합을 전체로 나눈 값.
3-3. 정밀도와 재현율
- 정밀도와 재현율은 Positive 데이터 셋(긍정으로 예측한 값)의 예측 성능에 좀 더 초점을 맞춘 지표이다. 이진 분류에서 사기 행위 예측, 암 검진 예측과 유사한 문제가 많은데, Positive로 예측한 값이 거의 없기 때문

- 정밀도(Precisioin)
- 정밀도(precision) = True Positive를 긍정으로 예측한 모든 값(TP+FP)으로 나눈 값이다.
- 그래서 정밀도는 긍정 예측 성능을 더 정밀하게 측정하기 위한 평가지표로, "양성 예측도"라고도 불린다.
- 정밀도가 중요 지표인 경우는 실제 음성인 데이터 예측을 양성으로 잘못 판단했을 때 타격이 큰 경우이다.
- 스팸 메일 여부를 판단하는 모델의 경우, 실제 스팸인 메일을 아니라고 분류하더라도 사용자가 불편함을 느끼는 정도이지만, 실제 스팸이 아닌데 스팸이라고 분류되는경우, 메일을 아예 받지못해서 업무에 차질이 생길 것.
- 정밀도(Precision) = 양성 예측도 = 예측이 긍정인 값에 초점 = (+)인데 (-)로 분류할 경우 타격이 큰 문제에 사용
- 따라서 FP를 낮추는데 초점을 맞춤 (-)인데 (+)로 분류 = FP
- 재현율(recall)
- 재현율(recall) = 역시 True positive이지만, 분모가 실제 값이 긍정인 모든 값 (TP+FN)이다.
- 그리고 재현율은 실제 값이 긍정인 모든 값이 분모라서, TPR(True Positive Rate)또는 민감도(Sensitivity)라 한다.
- 재현율이 중요 지표인 경우는 실제 Positive 양성 데이터를 Negative로 잘못 판단하게 되면 업무상 큰 영향이 발생하는 경우이다. (TPR, True값이 Positive인 값의 예측 성능에 초점을 맞춘 지표이므로)
- ex. 암 판단 모델 - 실제 암인 환자를 암이 아니라고 판단하면 오류의 대가가 생명을 앗아갈 정도로 크기 때문, 반면 실제 암이 아닌 환자를 암이라고 판단하면 재검사를 한번 더 하는 수준으로 큰 타격이 없음
- ex. 보험 사기와 같은 금융 사기 적발 모델 - 실제 금융거래 사기인데 아니라고 판단하면 회사에 미치는 손해가 큰 반면, 정상 금융거래인데 사기라고 잘못 판단하더라도, 재확인만 하면 된다. (단, 고객에게 금융 사기 혐의를 잘못 씌우면 문제가 될 수 있기에 정밀도도 중요한 지표이나, 회사 입장에서는 재현율이 더 중요)
- 보통은 재현율이 정밀도보다 상대적으로 중요한 업무가 많다.
- 재현율(Recall) = TRP = 민감도 = 실제가 긍정인 값에 초점 = (-)인데 (+)로 분류할 경우 타격이 큰 문제에 사용
- 따라서 FN을 낮추는데 초점을 맞춤 (+)인데 (-)로 분류 = FN
↓
- 이와 같은 성질 때문에 정밀도와 재현율은 보완적인 지표로 분류의 성능을 평가하는데 적용된다.
- 가장 좋은 성능 평가는 재현율과 정밀도 모두 높은 수치를 얻는 것, 반면 둘 중 하나만 높은 경우는 바람직하지 않음
- 타이타닉 예제에서 오차 행렬, 정밀도, 재현율을 모두 구해서 예측 성능을 평가해보자.
- 정밀도 계산 precision_score(), 재현율 계산 recall_score()
[In]
from sklearn.metrics import accuracy_score, precision_score, recall_score, confusion_matrixdef get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
print('오차 행렬')
print(confusion)
print('정확도: {0:.4f}, 정밀도:{1:.4f}, 재현율: {2:.4f}'.format(accuracy, precision, recall))# 원본 데이터 재로딩, 데이터 가공, 학습 데이터와 테스트 데이터 분할
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
titanic_df = pd.read_csv('train.csv')
y_titanic_df = titanic_df['Survived']
X_titanic_df = titanic_df.drop('Survived', axis=1)
X_titanic_df = transform_features(X_titanic_df)
X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, test_size = 0.20,
random_state=11)
# 이제 로지스틱 회귀로 예측하고 평가를 수행해보자.
lr_clf = LogisticRegression()
lr_clf.fit(X_train, y_train)
pred = lr_clf.predict(X_test)
get_clf_eval(y_test, pred)[Out]
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도:0.7742, 재현율: 0.7869정밀도(precision)이 재현율(recall)보다 낮게 나왔다. 재현율과 정밀도를 강화할 수 있는 방법에 대해 알아보자.
정밀도/제현율 트레이드 오프
- 분류의 결정 임곗값(Threshold)을 조정해, 정밀도 또는 재현율의 수치를 높일 수 있다.
- 하지만 두 지표는 상호보완적이라서, 한쪽을 높이면, 다른 하나의 수치는 떨어지기 쉬운데, 이 현상은 Trade-off라 함
- 분류 알고리즘은 예측 데이터가 특정 레이블(결정 크래스 값)에 속하는지를 계산하기 위해 먼저 개별 레이블별로 결정 확률을 구한다. 그리고 그 중 예측확률이 가장 큰 레이블 값으로 예측한다. (Threshold=0.5이면, 이 기준보다 크면 True, 작으면 False)
- 개별 데이터별로 예측 확률을 반환하는 메소드 predict_proba() - predict()와 유사하지만, 예측 결과 클래스값을 반환하는 것이 아니라, 예측 확률 결과를 반환한다. (ex. 1st column은 0 Negative의 확률, 2nd는 1 positive의 확률)
[In]
# 정밀도와 재현율을 높이기 위해 pred_proba() 사용
pred_proba = lr_clf.predict_proba(X_test) # classifier을 predict()하는 것처럼 preict_proba() 해주기
pred = lr_clf.predict(X_test) #위에서 반환할 확률 중(0과 1) 더 높은 확률 가진 값으로 최종 예측
print('pred proba() 결과 Shape: {0}'.format(pred_proba.shape))
print('pred_proba array에서 앞 3개만 샘플로 추출 \n:', pred_proba[:3])[Out]
pred proba() 결과 Shape: (179, 2)
pred_proba array에서 앞 3개만 샘플로 추출
: [[0.45891582 0.54108418] #1에 대한 확률
[0.87763358 0.12236642] #0에 대한 확률
[0.86854362 0.13145638]]import numpy as np
# 예측 확률 array와 예측 결괏값 array를 concatenatae해서 예측 확률,결괏값 한눈에 확인
pred_proba_result = np.concatenate([pred_proba, pred.reshape(-1,1)],axis=1)
print('두개의 class 중에서 더 큰 확률을 클래스 값으로 예측 \n', pred_proba_result[:3])[Out]
두개의 class 중에서 더 큰 확률을 클래스 값으로 예측
[[0.45891582 0.54108418 1. ]
[0.87763358 0.12236642 0. ]
[0.86854362 0.13145638 0. ]]- 반환 결과인 ndarray는 0과 1에 대한 확률을 나타내므로, 1번째 칼럼과 2번째 칼럼 값을 더하면 1이 된다.
- 맨 마지막 줄은 0과 1 중 더 큰 확류 값인 0으로 predict()메소드가 최종 예측하고있다.
- predict()는 predcit_proba()에 기반해 생성된 API이다.
- predict()는 predict_proba() 호출 결과로 반환된 배열에서 분류 결정 임곗값보다 큰 값이 들어있는 칼럼의 위치를 받아 최종적으로 예측 클래스를 결정하는 API
- 로직을 직접 구현하며, 정밀도 재현율 트레이드 오프 방식을 이해해보자.
- predict()는 predict_proba() 메소드가 반환하는 확률 값을 가진 ndarray에서 정해진 임곗값(앞에서는 0.5였음)을 만족하는 ndarray 칼럼 위치를 최종 예측 클래스로 결정.
- 이러한 구현을 위해 Binarizer 클래스를 이용하자
- threshold 변수를 특정 값으로 설정
- Binarizer 클래스를 객체로 생성
- 생성된 객체의 fit_transform() 메소드로 넘파이 ndarray를 입력하면 입력된 ndarray의 값을 지정된 threshold보다 같거나 작으면 0, 크면 1로 변환해 반환한다.
- 이 Binarizer을 이용해 사이킷런 predict()의 의사(psedo) 코드를 만들어보자. 바로 앞 예제의 lr(logistic regression)객체의 predict_proba() 메소드로 구한 각 클래스별 예측 확률값인 pred_proba 객체 변수에 분류 결정 임곗값을 0.5로 정한 Binaroizer 클래스를 적용해 최종 예측 값을 구하는 방식
- 구한 최종 예측 값에 대해 get_clf_eval() 함수를 적용해 평가지표 출력
[In]
from sklearn.preprocessing import Binarizer
X = [[1, -1, 2], [2, 0, 0], [0, 1.1, 1.2]]
# X의 개별 원소들이 threshold 값보다 같거나 작으면 0을, 크면 1 반환
binarizer = Binarizer(threshold=1.1) # binarizer 객체 생성
print(binarizer.fit_transform(X)) # fit_transform()[Out]
[[0. 0. 1.]
[1. 0. 0.]
[0. 0. 1.]]입력된 데이터셋 X에서 Binarizer의 threshold값이 1.1보다 같거나 작으면 0, 크면 1로 반환되었다.
[In]
from sklearn.preprocessing import Binarizer
# Binarizer의 threshold 설정값. 분류 결정 임곗값임
custom_threshold = 0.5
# predict_proba() 반환 값이 두 번째 칼럼, 즉 Positive 클래스(1) 칼럼 하나만 추출해 Binarizer 적용
pred_proba_1 = pred_proba[:,1].reshape(-1,1)
binarizer = Binarizer(threshold = custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test, custom_predict)[Out]
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도:0.7742, 재현율: 0.7869- 앞에서 학습하고 classifier 객체에서 호출된 predict()로 계산된 지표 값과 정확히 같다. predict()가 predict_proba()에 기반함을 알 수 있다.
- 분류 결정 임곗값을 0.4로 바꾸면 평가 지표가 어떻게 변할지 알아보자.
[In]
# Binarizer의 threshold 설정 값을 0.4로 설정
custom_threshold= 0.4
pred_proba_1 = pred_proba[:, 1].reshape(-1,1)
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_1)
custom_predict = binarizer.transform(pred_proba_1)
get_clf_eval(y_test,custom_predict)[Out]
오차 행렬
[[99 19]
[ 8 53]]
정확도: 0.8492, 정밀도:0.7361, 재현율: 0.8689- 임곗값을 낮추니 정밀도가 떨어지고, 재현율이 올라갔다. 분류 결정 임곗값은 Positive 예측값을 결정하는 확률의 기준이 되기 때문.
- 확률이 0.5가 아닌, 0.4부터 Positive로 예측을 너그럽게 하기 때문에 임곗값 값을 낮출수록 True 값이 많아지게 된다.
↔ Positive 예측값이 많아지면 재현율이 높아진다. (양성 예측을 많이해서 실제 양성을 음성으로 예측하는 횟수 ↓)

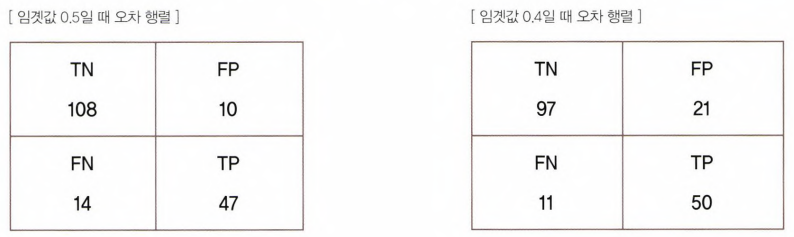
- 오차 행렬 우측 아래를 보면(TP), 임곗값이 0.5에서 0.4로 낮아지면서, TP가 50으로 늘었고, 좌측 아래(FN)를 보면, 11로 줄었다. 따라서 재현율이 좋아진 것
- 하지만 위쪽을 보면, FP는 21로 늘어서 (Posiitive로 더 예측했으니, 양성 예측 틀린 횟수도 당연히 늘어남), 정밀도가 많이 나빠졌다.
- 정확도도 줄어들었다.
- "분류 결정 임곗값(Threshold)이 낮아질수록 Positive로 예측할 확률이 높아짐, 재현율(TPR) 증가"**
- 이번에는 임곗값을 0.4부터 0.6까지 0.05씩 증가시키며 평가 지표를 조사해보자.
- get_eval_by_threshold( y_test, pred_proba_c1, thresholds ) 생성
[In]
# 테스트를 수행할 모든 임곗값을 리스트 객체로 저장
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]
def get_eval_by_threshold(y_test, pred_proba_c1, thresholds):
# thresholds 객체 내 값을 차례로 iterate, evaludation 수행
for custom_threshold in thresholds:
binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1)
custom_predict = binarizer.transform(pred_proba_c1)
print('임곗값:', custom_threshold)
get_clf_eval(y_test, custom_predict)
get_eval_by_threshold(y_test, pred_proba[:, 1].reshape(-1,1),thresholds)[Out]
임곗값: 0.4
오차 행렬
[[99 19]
[ 8 53]]
정확도: 0.8492, 정밀도:0.7361, 재현율: 0.8689
임곗값: 0.45
오차 행렬
[[100 18]
[ 12 49]]
정확도: 0.8324, 정밀도:0.7313, 재현율: 0.8033
임곗값: 0.5
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도:0.7742, 재현율: 0.7869
임곗값: 0.55
오차 행렬
[[109 9]
[ 15 46]]
정확도: 0.8659, 정밀도:0.8364, 재현율: 0.7541
임곗값: 0.6
오차 행렬
[[111 7]
[ 15 46]]
정확도: 0.8771, 정밀도:0.8679, 재현율: 0.7541위의 결과를 표로 정리
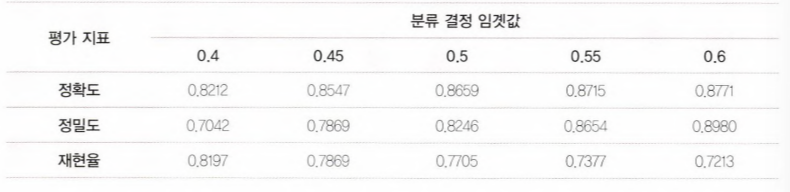
- True 기준 값(threshold)를 높일수록 정확도와 정밀도는 계속 올라가는 반면, 재현율은 계속 떨어진다.
- precision_recall_curve() API로도 확인 가능하다.
- -precision_recall_curve() 인자로 실제 값 데이터셋과 레이블 값이 1일 떄의 예측 확률 값을 입력한다.
- 레이블 값이 1일 때의 예측 확률 값은 predict_proba(X_test)[:, 1]으로, predict_proba()의 반환 ndarray의 2번째 칼럼값에 해당하는 데이터셋
- precision_recall_curve()는 일반적으로 0.11 ~ 0.95 정도의 임곗값을 담은 넘파이 ndarray와 이 임곗값에 해당하는 정밀도 및 재현율 값을 담은 ndarray 반환
- 반환된 임곗값의 데이터가 143건이라서, 샘플로 10건만 추출하되, 임곗값을 15단계로 추출해 좀 더 큰 값의 임곗값과, 그 때의 정밀도와 재현율을 살펴보자.
[In]
from sklearn.metrics import precision_recall_curve
# 레이블 값이 1일 때의 예측 확률 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
# 실제 값 데이터 셋과 레이블 값이 1일 때의 예측 확률을 precision_recall_curve 인자로 입력
precisions, recalls, thresholds = precision_recall_curve(y_test, pred_proba_class1)
print('반환된 분류 결정 임곗값 배열의 Shape:', thresholds.shape)
# d=반환된 임곗값 배열 로우가 143건이므로, 샘플로 10건만 추출하되, 임곗값을 15step으로
thr_index = np.arange(0, thresholds.shape[0], 15)
print('샘플 추출을 위한 임곗값 배열의 index 10개:', thr_index)
print('샘플 10개의 임곗값:', np.round(thresholds[thr_index],3))
# 15 step 단위로 추출된 임곗값에 따른 정밀도와 재현율 값
print('샘플 임곗값별 정밀도:', np.round(thresholds[thr_index],3))
print('샘플 임곗값별 재현율:', np.round(recalls[thr_index],3))[Out]
반환된 분류 결정 임곗값 배열의 Shape: (143,)
샘플 추출을 위한 임곗값 배열의 index 10개: [ 0 15 30 45 60 75 90 105 120 135]
샘플 10개의 임곗값: [0.105 0.119 0.134 0.181 0.258 0.408 0.573 0.675 0.824 0.948]
샘플 임곗값별 정밀도: [0.105 0.119 0.134 0.181 0.258 0.408 0.573 0.675 0.824 0.948]
샘플 임곗값별 재현율: [1. 0.967 0.918 0.902 0.902 0.836 0.754 0.607 0.377 0.148]- 역시나 임곗값이 증가할수록 (= True기준이 높아질수록 = 예측이 True인 값이 적어질수록)
정밀도값은 동시에 높아지나, 재현율 값은 낮아짐을 알 수 있다.
* 정밀도(Precision) = 양성 예측도 = 예측이 긍정인 값에 초점
* 재현율(Recall) = TRP = 민감도 = 실제가 긍정인 값에 초점
[In]
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
%matplotlib inline
def precision_recall_curve_plot(y_test, pred_proba_c1):
# threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출
precisions, recalls, thresholds = precision_recall_curve (y_test, pred_proba_c1)
# X축을 threshold 값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행,정밀도는 점선으로 표시
plt.figure(figsize=(8,6))
threshold_boundary = thresholds.shape[0]
plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
plt.plot(thresholds, recalls[0:threshold_boundary], label='recall')
# threshold 값 X축의 Scale을 0.1단위로 변경
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1),2))
# x축, y축 label과 legend, 그리고 grid 설정
plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
plt.legend(); plt.grid()
plt.show()
precision_recall_curve_plot ( y_test, lr_clf.predict_proba(X_test)[:, 1])[Out]
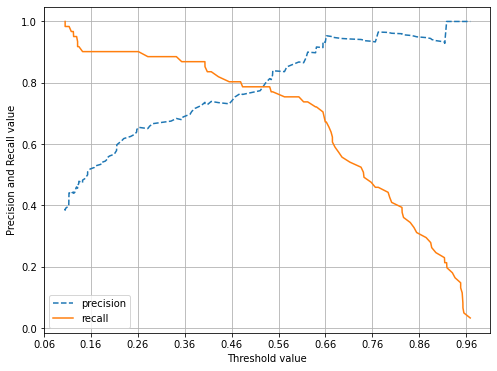
- 임곗값(Threshold value)이 낮을수록 많은 수의 양성 예측으로 인해,
재현율(recall,주황색 실선) 값이 극도로 높아지고, 정밀도(precision파란색 점선) 값이 극도로 낮아진다.
- 즉, 임곗값을 증가시킬수록(=True 예측 값이 적어질수록,) 정밀도(양성 예측도) 값이 높아지고, 재현율(True Positive Rate) 값이 낮아진다.
- "분류 결정 임곗값(Threshold)이 낮아질수록 Positive로 예측할 확률이 높아짐, 재현율(TPR) 증가"**
정밀도와 재현율의 맹점
정밀도와 재현율 두 수치를 상호보완할 수 있는 수준에서 적용되어야 하며, 단순히 하나의 성능 지표 수치를 높이기 위한 수단으로 사용해서는 안된다.
의미 없지만 정밀도(양성 예측도)가 100%되는 방법
- 확실한 기준이 되는 경우만 Positive로 예측, 나머지는 모두 Negative로 예측
- ex. 환자가 80세 이상, 이전에 암 진단을 받았고 암 세포의 크기가 상위 0.1%이상이면 무조건 Positive,나머지는 Negative로 예측
- 전체 환자 1000명 중 확실한 Positive 징후만 가진 환자는 단 1명, 이 한 명만 Positive로 예측하고, 나머지는 모두 Negative로 예측하더라도, FP는 0, TP는 1이되므로, 정밀도는 100%가 된다.
- 즉, 아주아주 확실한 사람만 Positive로 예측하여, 1000개 데이터 중 1개만 양성, 999개를 음성으로 예측, 그러면 Positive로 예측한 것 중 틀린게 아예 없으니 양성 예측도가 100%가 되는 것이다.
의미 없지만 재현율(TPR)이 100%되는 방법
- 모든 환자를 Positive로 예측하면 된다. 그러면 결과가 예측값인 것 중 맞는 개수가 최대로 나올 것이기 때문이다.
- 실제 양성인 사람이 30명 정도라도, 분모가 TP+FN, 즉 양성 예측이 맞는 경우와 음성 예측이 틀린 경우 (결과가 양성인 모든 경우)이므로, 음성으로 예측한 값이 0이니까, 음성으로 예측했는데 양성일 경우가 없으므로, 재현율이 100%가 되는 것이다.
→ 분류가 정밀도 또는 재현율 중 하나에 상대적인 중요도를 부여해, 각 예측 상황에 맞는 분류 알고리즘을 튜닝할 수 있지만, 정밀도/재현율 중 하나만 강조하는 상황이 되어서는 안된다. (ex. 암 예측 모델에서 재현율을 높인다고 대부분을 양성으로 무조건 판단할 경우, 환자의 부담이 매우 커질 것)
→ 정밀도와 재현율을 적절히 조합해서 분류의 종합적 성능평가에 사용할 수 있는 평가지표가 필요
3-4. F1 스코어

- F1스코어는 정밀도와 재현율을 결합한 지표이다. 정밀도와 재현율이 어느 한쪽으로 치우치지 않는 수치를 나타낼 때, 상대적으로 높은 값을 가진다.
- 만약 A모델이 정밀도가 0.9, 재현율이 0.1로 극단적인 차이가 나고, B 예측 모델은 정밀도가 0.5, 재현율이 0.5로 정밀도와 재현율에 큰 차이가 없다면, F1스코어는 0.18이고, B 예측 모델의 F1 스코어는 0.5로 B모델이 A모델에 비해 매우 우수한 F1스코어를 가진다.
- f1_score() API를 사용한다.
[In]
# f1 스코어
from sklearn.metrics import f1_score
f1 = f1_score(y_test, pred)
print('F1 스코어: {0:.4f}'.format(f1))[Out]
F1 스코어: 0.7805- 임곗값을 변화시키면서 F1스코어를 포함한 평가 지표를 구해보자.
- 앞서 만든 함수 get_clf_eval() 함수에 F1스코어를 구하는 로직 추가
[In]
def get_clf_eval(y_test, pred):
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
#F1 스코어 추가
f1 = f1_score(y_test, pred)
print('오차 행렬')
print(confusion)
#F1 스코어 print 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},F1:{3:.4f}'.format(accuracy, precision, recall, f1))thresholds = [0.4, 0.45, 0.5, 0.55, 0.60]
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test, pred_proba[:, 1].reshape(-1,1), thresholds)[Out]
임곗값: 0.4
오차 행렬
[[99 19]
[ 8 53]]
정확도: 0.8492, 정밀도: 0.7361, 재현율: 0.8689,F1:0.7970
임곗값: 0.45
오차 행렬
[[100 18]
[ 12 49]]
정확도: 0.8324, 정밀도: 0.7313, 재현율: 0.8033,F1:0.7656
임곗값: 0.5
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869,F1:0.7805
임곗값: 0.55
오차 행렬
[[109 9]
[ 15 46]]
정확도: 0.8659, 정밀도: 0.8364, 재현율: 0.7541,F1:0.7931
임곗값: 0.6
오차 행렬
[[111 7]
[ 15 46]]
정확도: 0.8771, 정밀도: 0.8679, 재현율: 0.7541,F1:0.8070위 결과를 도표로 정리
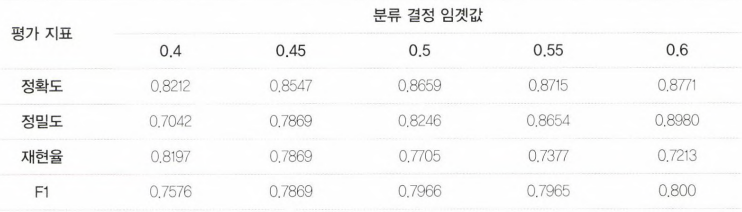
- F1 스코어는 임곗값이 0.6일 때 가장 좋은 값을 보여준다. 하지만, 임곗값이 0.6인 경우에는 재현율이 크게 감소한다.
3-5. ROC 곡선과 AUC
참고 필기

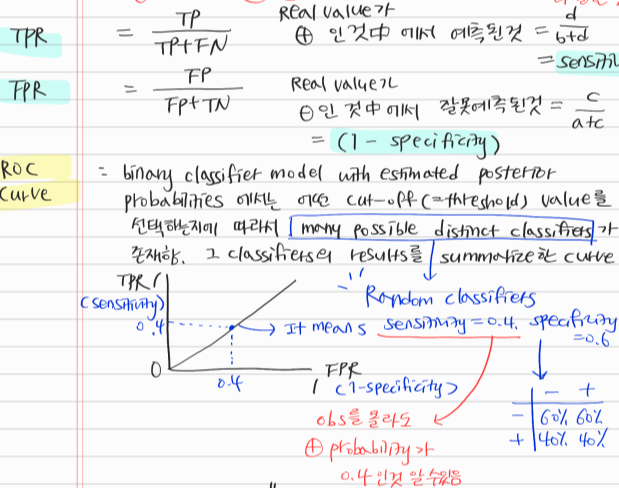


- ROC 곡선과 이에 기반한 AUC 스코어는 이진 분류의 예측 성능 측정에서 중요하게 사용되는 지표이다.
- ROC는 Reveiver Operation Characteristic Curve
- 의학 분야에서 많이 사용되지만, 머신러닝의 이진 분류 모델의 예측 성능을 판단하는 중요한 평가 지표이기도 하다.
- ROC 곡선은 FPR(False Positive Rate)이 변할 때, TPR(True Positive Rate)이 어떻게 변하는지를 나타내는 곡선이다.
- FPR을 X축, TPR이 Y축으로 잡으면, FPR의 변화에 따른 TPR의 변화가 곡선 형태로 나타난다.
- TPR은 앞서 보았듯이 재현율을 의미한다.(=민감도) * 민감도에 대응하는 지표로 TNR(=특이성)이 있다.
- TPR(=재현율=민감도)은 실젯값이 양성,즉 실젯값이 양성으로 정확히 예측되어야하는 수준을 나타낸다. (질병이 있는 사람은 있다고 판정)
- TNR(=특이성)은 실젯값이 음성, 즉 실젯값이 음성으로 정확히 예측되어야하는 수준을 나타낸다. (질병이 없는 건강한 사람은 질병이 없는 것으로 음성 판정)
- X축에 오는 FPR는 특이성을 1에서 뺀 값이다. FPR = (1-Specificity)
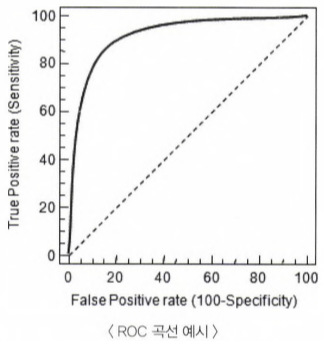
- 가운데 점선은 ROC 곡선의 최저값이다.
- 왼쪽 하단과 오른쪽 상단을 대각선으로 이은 직선은 동전을 무작위로 던져 앞/뒤를 맞추는 랜덤 수준의 이진분류의 ROC직선이다.(즉, accuracy=0.5)
- ROC 곡선이 가운데 직선에 가까울수록 성능이 떨어지는 것이며, 멀어질수록 성능이 뛰어난 것이다.
- ROC 곡선은 FPR을 0부터 1까지 변경하면서, TPR(재현율=민감도)의 변화 값을 구한다.
- FPR을 변경하는 방법은 '분류 결정 임곗값(Threshold)을 변경하는 것'
- Threshold는 Positive 예측 값을 결정하는 확률의 기준이기 때문에, FPR을 0으로 만들려면, 임곗값을 1로 지정해서 Positive 예측 기준을 높게 만들어, Classifier(분류기)가 임곗값보다 높은 확률을 가진 데이터를 Positive로 예측하는 것이 불가능하여, FPR 틀릴 Positive가 존재하지 않기에, 0이 되기 때문이다.
- 반대로 FPR을 1로 만들려면, 임곗값을 0으로 지정해서, Positive 확률 기준이 너무 낮아져 전부 다 Positive로 예측하게되고, 그러면 긍정으로 예측해서 틀릴 확률(FPR)은 1이 된다.
- roc 곡선을 구하기위해 roc_curve() 를 사용한다. precision_recall_curve()와 유사하다.

roc_curve()로 타이타닉 생존자 예측 모델의 FPR, TPR, 임곗값을 구해보자.
[In]
from sklearn.metrics import roc_curve
# 레이블 값이 1일 때의 예측 확률 추출
pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
FPRs, TPRs, thresholds = roc_curve(y_test, pred_proba_class1)# 반환된 임곗값 배열 로우가 47건이므로 샘플로 10건만 추출하되, 임곗값을 5 step으로 추출
# thresholds[0]은 max(예측 확률)+1로 임의설정된다.
# 이를 제외하기 위해 np.arange는 1부터 시작, thr_index = np.arange(1, thresholds.shape[0],5)
thr_index = np.arange(1, thresholds.shape[0], 5)
print('샘플 추출을 위한 임곗값 배열의 index 10개:', thr_index)
print('샘플용 10개의 임곗값:', np.round(thresholds[thr_index], 2))
# 5 step 단위로 추출된 임곗값에 따른 FPR, TPR 값
print('샘플 임곗값별 FPR:', np.round(FPRs[thr_index], 3))
print('샘플 임곗값별 TPR:', np.round(TPRs[thr_index], 3))[Out]
샘플 추출을 위한 임곗값 배열의 index 10개: [ 1 6 11 16 21 26 31 36 41 46]
샘플용 10개의 임곗값: [0.97 0.66 0.64 0.55 0.45 0.34 0.15 0.13 0.12 0.11]
샘플 임곗값별 FPR: [0. 0.017 0.042 0.076 0.153 0.212 0.449 0.559 0.644 0.737]
샘플 임곗값별 TPR: [0.033 0.672 0.721 0.77 0.803 0.885 0.902 0.934 0.967 0.984]- 임곗값이 1에 가까운 점에서 점점 작아지면서, FPR은 커지고, TPR은 더 가파르게 커진다.
ROC 곡선을 그려보자.
[In]
def roc_curve_plot(y_test, pred_proba_c1):
# 임곗값에 따른 FRP, TRP 반환받기
FPRs, TPRs, thresholds = roc_curve(y_test, pred_proba_c1)
# ROC 곡선을 그래프 곡선으로 그림
plt.plot(FPRs, TPRs, label='ROC')
# 가운데 대각선 직선을 그림
plt.plot([0,1], [0,1], 'k--', label='Random')
# FPR X축의 스케일을 0,1단위로 변경, X축 Y축 이름 설정
start, end = plt.xlim()
plt.xticks(np.round(np.arange(start, end, 0.1), 2))
plt.xlim(0,1); plt.ylim(0,1)
plt.xlabel('FPR(1-Sensitivity)'); plt.ylabel('TPR(Recall)')
plt.legend()
roc_curve_plot(y_test, pred_proba[:, 1])[Out]

* AUC (Area Under Curve)
- ROC 곡선 자체는 FPR과 TPR의 변화값을 보는데 이용하는 것이고, 분류의 성능 지표로 사용되는 것은 ROC 곡선 면적에 기반한 AUC값이다.
- AUC값은 ROC 곡선 밑의 면적을 구한 것으로 일반적으로 1에 가까울 수록 좋은 수치이다.
- AUC가 커지려면 FPR이 작은 상태에서 얼마나 큰 TPR(=Recdall-=Y축)을 얻을 수 있느냐가 관건이다.
- 가운데 직선에서 멀어지고, 왼쪽 상단 모서리쪽으로 가파르게 곡선이 이동할수록 직사각형에 가까운 곡선이 되어 면적이 1에가까워지는 좋은 ROC AUC 성능 수치를 얻게된다.
- 0.5 이상의 AUC값을 가진다.
[In]
from sklearn.metrics import accuracy_score, confusion_matrix, precision_score
from sklearn.metrics import recall_score, f1_score, roc_auc_score
import numpy as np
print(confusion_matrix(y_target, preds))
print("정확도:", np.round(accuracy_score(y_target, preds),4))
print("정밀도:", np.round(precision_score(y_target, preds),4))
print("재현율:", np.round(recall_score(y_target, preds),4))[Out]
[[7668 4832]
[3636 8864]]
정확도 : 0.6613
정밀도: 0.6472
재현율 : 0.7091- 타이타닉 생존자 예측 회귀모델의 ROC AUC값은 약 0.8987
- 마지막으로 get_clf_eval() 함수에 roc_auc_socre()을 추가하자.
- ROC AUC는 예측 확률값을 기반으로 계산되므로, 이를 get_clf_eval() 함수의 인자로 받을 수 있도록 get_clf_eval(y_test, pred=None, pred_proba = None)로 함수형을 변경해준다.
def get_clf_eval(y_test, pred=None, pred_proba=None):
# roc_auc가 예측 확률값 기반으로 계산될 수 있도록 인자를 pred=None, pred_proba=None으로 변경
confusion = confusion_matrix(y_test, pred)
accuracy = accuracy_score(y_test, pred)
precision = precision_score(y_test, pred)
recall = recall_score(y_test, pred)
f1 = f1_score(y_test, pred)
# ROC-AUC 추가
roc_auc = roc_auc_score(y_test, pred_proba)
print('오차 행렬')
print(confusion)
# ROC-AUC 추가
print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}, \
F1 : {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))위 함수를 아래 예제에서 적용시켜보자.
3-6. 파마 인디언 당뇨병 예측
- 파마 인디언 당뇨병 데이터 세트 구성 피처
- Pregnancies 임신 횟수
- Glucose 포도당 부하 검사 수치
- BloodPressure 혈압(mm Hg)
- SkinThickness 팔 삼두근 뒤쪽의 피하지방 측정값(mm)
- Insulin 혈청 인슐린 (mu U/ml)
- BMI 체질량 지수(체중kg/키m^2)
- DiabetesPedigreeFunction 당뇨 내력 가중치 값
- Age
- Outcome 클래스 결정값 (0 또는 1)
[In]
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, roc_auc_score
from sklearn.metrics import f1_score, confusion_matrix, precision_recall_curve, roc_curve
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
diabetes_data = pd.read_csv('diabetes.csv')
print(diabetes_data['Outcome'].value_counts())
diabetes_data.head(3)[Out]
0 500
1 268
Name: Outcome, dtype: int64
Pregnancies Glucose BloodPressure SkinThickness Insulin BMI DiabetesPedigreeFunction Age Outcome
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1- 전체 768개의 데이터 중에서 Negative 값 0이 500개, Positive 값 1이 268개로 Negative가 상대적으로 많다.
[In]
diabetes_data.info()[Out]
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 768 entries, 0 to 767
Data columns (total 9 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Pregnancies 768 non-null int64
1 Glucose 768 non-null int64
2 BloodPressure 768 non-null int64
3 SkinThickness 768 non-null int64
4 Insulin 768 non-null int64
5 BMI 768 non-null float64
6 DiabetesPedigreeFunction 768 non-null float64
7 Age 768 non-null int64
8 Outcome 768 non-null int64
dtypes: float64(2), int64(7)
memory usage: 54.1 KB- 0 Null값은 없으며, 피처 타입은 모두 숫자형이다. 임신횟수, 나이와 같은 숫자형 피처와 당뇨검사 수치 피처로 구성된 특징으로 볼 때, 별도의 피처 인코딩은 필요하지 않아보인다.
# 피처 데이터셋 X, 레이블 데이터셋 Y 추출
# 맨 끝이 Outcome 칼럼으로 레이블 값임. 칼럼 위치 -1을 이용해서 추출
X = diabetes_data.iloc[:, :-1]
y = diabetes_data.iloc[:, -1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=156,stratify=y)- 로지스틱 회귀로 학습, 예측 및 평가를 수행해보자.
lr_clf = LogisticRegression()
lr_clf.fit(X_train,y_train)
pred = lr_clf.predict(X_test)
pred_proba = lr_clf.predict_proba(X_test)[:,1]
get_clf_eval(y_test, pred, pred_proba)[Out]
오차 행렬
[[88 12]
[23 31]]
정확도: 0.7727, 정밀도: 0.7209, 재현율: 0.5741, F1 : 0.6392, AUC:0.7919- 정확도는 77.27%, 재현율은 57.41%로 측정되었다.
- 전체 데이터의 65%가 Negative이므로 불균형 데이터, 따라서 정확도 보다는 재현율에 초점 (당뇨병 예측문제니까, 당뇨병인데 아니라고 예측하면 문제가 커짐, 즉 FNR을 낮추는것이 중요 → 결괏값이 True인것에 초점을 맞춘 재현율을 지표로)
- 먼저 정밀도 재현율 곡선을 보고 임곗값별 정밀도와 재현율 값의 변화를 확인해보자. (앞서 만든 precision_recall_curve_plot()함수 이용
[In]
pred_proba_c1 = lr_clf.predict_proba(X_test)[:,1]
precision_recall_curve_plot(y_test, pred_proba_c1)[Out]
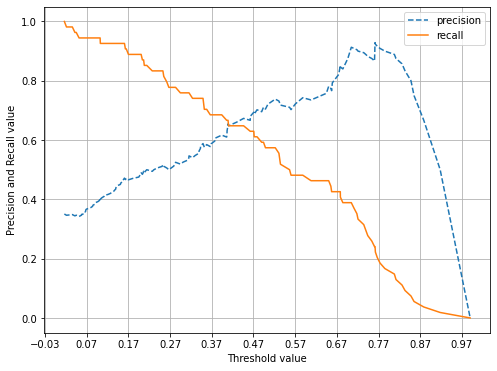
- 임곗값이 0.42일 때 두 곡선이 만나기에, 0.42로 낮추면 정밀도와 재현율이 어느 정도 균형을 맞출 것으로 보인다.
- 하지만, 두 개의 지표 모두 0.7이 안 되는 수치이다. 여전히 두 지표의 값이 낮기 때문에 임곗값 조정 전 데이터를 재점검해보자. → 피처 값의 분포도 살펴보기
# Threshold=0.42에서 균형을 이루긴하나, 여전히 낮은 수치, 피처를 재점검해보자
diabetes_data.describe()[Out]
Pregnancies Glucose BloodPressure SkinThickness Insulin BMI DiabetesPedigreeFunction Age Outcome
count 768.000000 768.000000 768.000000 768.000000 768.000000 768.000000 768.000000 768.000000 768.000000
mean 3.845052 120.894531 69.105469 20.536458 79.799479 31.992578 0.471876 33.240885 0.348958
std 3.369578 31.972618 19.355807 15.952218 115.244002 7.884160 0.331329 11.760232 0.476951
min 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.078000 21.000000 0.000000
25% 1.000000 99.000000 62.000000 0.000000 0.000000 27.300000 0.243750 24.000000 0.000000
50% 3.000000 117.000000 72.000000 23.000000 30.500000 32.000000 0.372500 29.000000 0.000000
75% 6.000000 140.250000 80.000000 32.000000 127.250000 36.600000 0.626250 41.000000 1.000000
max 17.000000 199.000000 122.000000 99.000000 846.000000 67.100000 2.420000 81.000000 1.000000- min()이 0으로 되어있는 피처가 상당히 많다. 예를 들어 Glucose는 포도당 수치인데 min값이 0인건 말이되지 않음.
# Glucose 가 min()이 0인건 말이 되지 않는다. 히스토그램으로 확인해보자
plt.hist(diabetes_data['Glucose'],bins=10)
- min()값이 0으로 되어있는 피처에 대해, 0 값의 건수 및 전체 데이터 건수 대비 몇 퍼센트의 비율로 존재하는지 확인해보자. 확인할 피처는 Glucose, BloodPressure, SkinThickness, Insulin, BMI (Pregnancies는 임신'횟수'이므로 제외)
[In]
# 0값을 검사할 피처명 리스트
zero_features = ['Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI']
# 전체 데이터 건수
total_count = diabetes_data['Glucose'].count()
# 피처별로 반복하면서 데이터 값이 0인 데이터 건수를 추출하고, 퍼센트 계산
for feature in zero_features:
zero_count = diabetes_data[diabetes_data[feature] == 0][feature].count()
print('{0} 0 건수는 {1}, 퍼센트는 {2:.2f} %'.format(feature, zero_count, 100*zero_count/total_count))[Out]
Glucose 0 건수는 5, 퍼센트는 0.65 %
BloodPressure 0 건수는 35, 퍼센트는 4.56 %
SkinThickness 0 건수는 227, 퍼센트는 29.56 %
Insulin 0 건수는 374, 퍼센트는 48.70 %
BMI 0 건수는 11, 퍼센트는 1.43 %- SkinThickness 와 Insulin의 0값은 각각 전체의 29.56%, 48.7%로 매우 많다.
- 전체 데이터 건수가 많지 않기 때문에, 이들 데이터를 일괄적으로 삭제할 경우에는 학습을 효과적으로 수행하기 어렵다. 따라서 0값을 '평균값'으로 대체해보자.
# zero_feuaters 리스트 내부에 저장된 개별 피처들에 대해 0값을 평균 값을 대체
mean_zero_features = diabetes_data[zero_features].mean()
diabetes_data[zero_features] = diabetes_data[zero_features].replace(0, mean_zero_features)- 이제 0값을 평균값으로 대체한 데이터 세트에 피처 스케일링을 적용해 변환하자.
- 로지스틱 회귀의 경우, 일반적으로 숫자 데이터에 스케일링을 적용하는 것이 좋다.
- 이후에 다시 학습/테스트 데이터세트로 나누고, 로지스틱 회귀를 적용해 성능평가 지표를 확인해보자.
X = diabetes_data.iloc[:, :-1]
y = diabetes_data.iloc[:, -1]
# StandardScaler 클래스를 이용해 피처 데이터셋에 일괄적으로 스케일링 적용
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=156, stratify=y)# 로지스틱 회귀로 학습-예측-평가 수행
lr_clf = LogisticRegression()
lr_clf.fit(X_train, y_train)
pred = lr_clf.predict(X_test)
pred_proba = lr_clf.predict_proba(X_test)[:, 1]
get_clf_eval(y_test, pred, pred_proba)[Out]
오차 행렬
[[90 10]
[21 33]]
정확도: 0.7987, 정밀도: 0.7674, 재현율: 0.6111, F1 : 0.6804, AUC:0.8433- '데이터 변환'과 '스케일링'을 통해 성능 수치가 일정 수준 개선되었다. (로지스틱 회귀에 대해 아직 깊게 배우지 않아 하이퍼 파라미터 튜닝은 생략함)
- 하지만 여전히 재현율이 낮다. 분류 결정 임곗값 Threshold를 변화시키며 재현율 수치가 어느정도 개선되는지 확인해보자.
- 임곗값을 0.3부터 0.5까지 변화시키면서 재현율과 다른 평가지표의 값의 변화를 출력해보자.
(재현율(TPR)은 True로 예측을 적게 할수록 높아지므로, 임곗값이 커질수록 개선될 것)
- 임곗값에 따른 평가 수치 출력은 앞서 사용한 get_eval_by_threshold() 함수 이용
:
thresholds = [0.4, 0.45, 0.50, 0.55, 0.60]
def get_eval_by_threshold(y_test, pred_proba_c1, thresholds): # thresholds 객체 내 값을 차례로 iterate, evaludation 수행 for custom_threshold in thresholds: binarizer = Binarizer(threshold=custom_threshold).fit(pred_proba_c1) custom_predict = binarizer.transform(pred_proba_c1) print('임곗값:', custom_threshold) get_clf_eval(y_test, custom_predict)get_eval_by_threshold(y_test, pred_proba[:, 1].reshape(-1,1),thresholds)
[In]
# 재현율 개선을 위해 임곗값을 0.3부터 0.5까지 변화
thresholds = [0.3, 0.33, 0.36, 0.39, 0.42, 0.45, 0.48, 0.50]
pred_proba = lr_clf.predict_proba(X_test)
get_eval_by_threshold(y_test, pred_proba[ : , 1].reshape(-1, 1), thresholds)
# 에러난당,,[Out] output 정리

- 위 표를 근거로 하면 정확도와 정밀도를 희생하고 재현율을 높이는 데 가장 좋은 임곗값은 0.33으로, 재현율 값이 0.7963이다.
- 하지만 정밀도가 0.5972로 매우 저조해졌으니 극단적인 선택
- 임곗값 0.48이 전체적인 성능 평가 지표를 유지하면서 재현율을 약간 향상시키는 좋은 임곗값
- 임곗값 0.48일 경우 정확도는 0.7987, 정밀도는 0.7447, 재현율은 0.6481, F1 스코어는 0.6931, ROC AUC는 0.8433
- 임곗값을 0.48로 낮춘 상태에서 다시 예측을 해보자.
- 사이킷런의 predict() 메소드는 임곗값을 마음대로 변환할 수 없어 별도의 로직으로 이를 구현해야한다.
- Binarizer 클래스를 이용해 predict_proba()로 추출한 예측 결과확률값을 변환해, 변경된 임곗값에 따른 예측 클래스값을 구해보자.
[In]
# 임곗값을 0.48로 설정한 Binarizer 생성
binarizer = Binarizer(threshold=0.48)
# 위에서 구한 lr_clf의 predict_proba() 예측 확률 array에서 1에 해당하는 칼럼값을 Binarizer변환
pred_th_048 = binarizer.fit_transform(pred_proba[:, 1].reshape(-1,1))
get_clf_eval(y_test, pred_th_048, pred_proba[:, 1])[Out]
오차 행렬
[[88 12]
[19 35]]
정확도: 0.7987, 정밀도: 0.7447, 재현율: 0.6481, F1 : 0.6931, AUC:0.84333-7. 정리
1. (특히) 이진 분류의 레이블 값이 불균형하게 분포될 경우, 단순히 예측 결과와 실제 결과가 일치하는 지표의 정확도만으로는 예측성능 평가 불가
2. 오차행렬은 Negative와 Positive 값을 가지는 실제 클래스 값과 예측 클래스 값이 True와 False에 따라 TN, FP, FN, TP로 매핑되는 4분면 행렬을 기반으로 예측 성능평가, 이를 통해 예측 성능의 오류 발생을 파악 할 수 있음
3. 정밀도와 재현율은 'Positive; 데이터셋의 예측 성능에 초점, 재현율은 암 양성 예측 모델과 같이 실제값이 Positive인 데이터 예측을 아니라고 할시 타격이 큰 경우에 더 중요한 지표
4. 분류하려는 업무의 특성상 정밀도또는 재현율이 특별히 강조 되어야 할 경우, 분류의 결정 임곗값(Threshold) 조정을 통해 정밀도 또는 재현율 수치를 높이는 방법에 대해 배움
5. F1스코어는 정밀도와 재현율을 결합한 평가 지표, 둘 다 어느 한쪽으로 치우치지않을 때 높은 F1스코어를 갖게 됨
6. ROC-AUC는 일반적으로 이진 분류의 성능 평가를 위해 가장 많이 사용됨. AUC는 1에 가까울 수록 좋은 수치
'데이터 분석 > 파이썬 머신러닝 완벽가이드' 카테고리의 다른 글
| [8] 파이썬 머신러닝 완벽 가이드 - 4. 분류(랜덤 포레스트, GBM, XGBOOST, LIGHT GBM) (0) | 2022.08.17 |
|---|---|
| [7] 파이썬 머신러닝 완벽 가이드 - 4. 분류(결정 트리-제약을 통한 과적합 해결, 앙상블-보팅-소프트 보팅과 하드 보팅) (0) | 2022.08.15 |
| [5] 파이썬 머신러닝 완벽가이드 - 사이킷런 데이터 전처리, 타이타닉 예제, 정리 (0) | 2022.08.10 |
| [4] 파이썬 머신러닝 완벽가이드 - 판다스(데이터 핸들링) 마무리, 사이킷런 모듈 연습 마무리(Stratified K fold, GridSearchCV) (0) | 2022.08.06 |
| [3] 파이썬 머신러닝 완벽가이드 - 판다스(데이터 핸들링) (0) | 2022.08.05 |




