| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- XGBoost
- 로그 변환
- WITH ROLLUP
- Growth hacking
- python
- sql
- 분석 패널
- 인프런
- lightgbm
- 스태킹 앙상블
- ARIMA
- 캐글 산탄데르 고객 만족 예측
- 데이터 증식
- splitlines
- 그로스 해킹
- 리프 중심 트리 분할
- 3기가 마지막이라니..!
- 캐글 신용카드 사기 검출
- ImageDateGenerator
- DENSE_RANK()
- 데이터 정합성
- 그룹 연산
- 그로스 마케팅
- 부트 스트래핑
- 컨브넷
- tableau
- WITH CUBE
- pmdarima
- 마케팅 보다는 취준 강연 같다(?)
- 데이터 핸들링
- Today
- Total
LITTLE BY LITTLE
[4-2] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 본문

목차
<4장. 유용한 선형회귀>4.1 선형회귀의 필요성4.1.1 모델이 필요한 이유4.1.2 A/B테스트와 회귀분석4.1.3 회귀분석을 통한 보정
4.2 회귀분석 이론4.2.1 단순선형회귀4.2.2 다중선형회귀
4.3 프리슈-워-로벨 정리와 직교화
4.3.1 편향 제거 단계4.3.2 잡음 제거 단계4.3.3 회귀 추정량의 표준오차4.3.4 최종 결과 모델4.3.5 FWL 정리 요약
4.4 결과 모델로서의 회귀분석
4.5 양수성과 외삽
4.6 선형회귀에서의 비선형성
4.6.1 처치 선형화
4.6.2 비선형 FWL과 편향 제거
4.7 더미변수를 활용한 회귀분석
4.7.1 조건부 무작위 실험
4.7.2 더미 변수
4.7.3 포화회귀모델
4.7.4 분산의 가중평균과 회귀분석
4.7.5 평균 제거와 고정효과
4.8 누락 변수 편향
4.9 중립 통제변수
4.9.1 잡음 유발 통제변수
4.9.2 특성 선택: 편향-분산 트레이드오프
4.10 요약
이번 장에서는 중요한 편향 제거 기법인 1. 선형 회귀, 2. 최소 제곱법(OLS), 3. 직교화를 다루고, 선형 회귀에서 비롯된 개념인 4. 처치 직교화라는 개념을 배운다. 이 개념은 인과추론에 머신러닝 모델을 사용할 때 유용하게 쓰임
4.4 결과 모델로서의 회귀분석
이번 절 내내 회귀분석은 '처치를 직교화하는 방식'임을 강조하고 있다. 하지만, 회귀분석은 "잠재적 결과를 대체(imputation)하는 방법"이기도 하다.
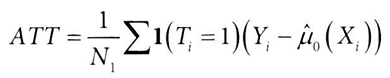
* I(.) 지시 함수(Indicator Function): 안에 있는 인수가 참이면 1을 반환하고, 그렇지 않으면 0을 반환하는 함수
- 처치가 0또는 1의 이진값을 주어졌을 때, 대조군(T=0)에서 X에대한 Y의 회귀분석이 E[Y|X]를 잘 근사한다면, 해당모델을 이용해 Y0을 대체하고, ATT를 추정할 수 있음
- 마찬가지로 실험군에서도 E[Y1|X]를 잘 모델링할 수 있다면, 대조군에서의 평균효과(ATE)를 추정할 수 있다.

- 위의 추정량으로 잠재적 결과 모두를 대체할 수 있고, 대체하는 것은 곧 Y를 X와 T에 모두 회귀하고 T에 대한 매개변수 추정값을 얻는 것과 동일하다. (이전까지 배운 처치를 직교화했던 과정)
- 또한, 누락된 잠재적 결과를 대체할 수도 있다.

→ 회귀분석은 "전체 처치 반응 함수를 대체하는 것"으로 이해할 수 있다.
→ 잠재적 결과 Y(t)를 선처럼 대체하는 것이 포함됨
*전체 처치 반응 함수: 연속형 처치의 다양한 수준에 대한 결과의 기댓값으로, 처치 수준의 변화가 결과에 어떤 영향을 미치는지 설명한다. 회귀분석을 통해 이 함수를 추정하여 인과효과를 분석하는 것
✅ 회귀분석은 이중강건하다.
: E[T|X]를 정확하게 추정하여 직교화할 수 있거나, 잠재적 결과 E[Yt|X]를 정확하게 추정할 수 있다는 사실
(추후 5장에서 깊이다루며, 4부의 이중차분법을 배울 때 이러한 관점이 중요하다.)
✅ EX. 사립학교 재학(T)이 개인의 소득(Y)에 영향을 미칠까?
- 사립학교 졸업생은 흔히 공립학교 졸업생보다 더 돈을 많이 번다.
- 교란 요인이 될 수 있는 요인
- 부모 소득 - 부유한 가정의 자녀는 사립학교에 진학할 확률이 높다.
- SAT 점수 - 사립학교는 학생을 선별적으로 뽑아 애초에 뛰어난 학생들만 받는다.
- 따라서 단순히 Y(소득)을 T(사립학교 더미변수)에 회귀한다면, 양의 효과를 보일 것
- 이 사례에서 SAT 점수와 부모의 소득을 보정하면, 측정된 효과는 감소한다.


하지만 보정된 결과에서도 여전히 사립학교의 효과는 유의했다.
마지막으로 통제 변수로 '학생들이 지원한 학교의 평균 SAT점수(=학생들의 포부를 나타내는 대리변수)'를 추가한 결과, 유의하지 않음

심지어 마지막 통제 변수만 유지하고, 델타1,2(SAT점수와 부모 소득 통제 변수)를 제외해도 여전히 유의하지 않은 추정값이 나옴
→ 해석하면, 학생의 포부 수준(AvgSATSchool)을 고려하면, 공립학교나 사립학교에 다니는 것이 적어도 소득(Y)측면에서는는 중요하지 않음을 나타냄

4.5 양수성과 외삽
*외삽(extrapolation): 이전의 경험과 실험으로부터 얻은 데이터에 비추어 예측해보는 기법
회귀분석은 잠재적 결과를 모수적으로 모델링하므로, 처치범위 이외에 대해서 외삽을 할 수 있다.
✅ 외삽은 합리적인지에 따라서 축복이 될 수도 있고, 저주가 될 수도 있다(*양수성 가정)
양수성 가정이 충족되지 않을 경우 회귀분석은 외삽을 통해 해당 가정이 충족되지 않은 영역을 대체하게 됨
- 예를 들어, 중첩(overlap)이 적은 데이터셋1에서 처치효과(T)를 추정해야 한다고 가정할 때,
- 데이터셋1에서 공변량X값이 클 때에는 대조군이 존재하지 않고, 반대로 작으면 실험군이 없음
- 이 데이터에 회귀분석으로 T를 추정하면, 아래와 같이 Y0과 Y1을 추정
데이터셋1
# 데이터셋1
np.random.seed(1)
n = 1000
x = np.random.normal(0, 1, n)
t = np.random.normal(x, 0.2, n) > 0
y0 = x
y1 = 1 + x
y = np.random.normal((1-t)*y0 + t*y1, 0.2)
데이터셋2
y0 = x * (x<0) + (x>0)*0
→ 데이터셋2에서는 y0 정의 시 x값이 0보다 작은 경우를 포함한다. (양수성 가정 위배)
→ 따라서 y0는 x값이 음수인 경우에는 x값을 유지하고, 양수인 경우에는 0으로 설정됨.
# 데이터셋2
np.random.seed(1)
n = 1000
x = np.random.normal(0, 1, n)
t = np.random.binomial(1, 0.5, size=n)
y0 = x * (x<0) + (x>0)*0 # 데이터셋2에서는 양수성 가정이 충족되지 않은 영역이 나타남
y1 = 1 + x
y = np.random.normal((1-t)*y0 + t*y1, 0.2)
df_pos = pd.DataFrame(dict(x=x,t=t.astype(int),y=y))
- 데이터셋1 - 공변량 공간 전반에 중첩이 있는 결과 추세선이 비슷하다면, 약간의 외삽은 문제가 되지 않는다.
- 데이터셋2 - X가 양수일 때 효과가 점점 커진다. 따라서, 전에 적합시킨 모델을 데이터셋2에 대해 평가하면 T의 실제 효과보다 T의 효과를 과소평가했음을 알 수 있다.
- 즉, 양수성 가정이 충족되지 않는(=특정 처치를 전혀 받지 않을 확률이 있는) 범위에서의 T의 효과는 정확히 알 수 없다.
- 따라서, 이러한 범위에 대해서 외삽을 통해 가정이 충족되지 않은 영역을 대체하게 되는 것이고, 외삽은 신뢰할 수도 있지만, 위험을 감수해야 할 것
4.6 선형회귀에서의 비선형성
이제껏 본 사례들은 처치 반응 곡선이 선형적이었다.
(ex. 신용한도가 1,000에서 2,000으로 늘어날 때와 2,000에서 3,000으로 늘어날 때 같은 정도의 위험이 증가)
하지만 실제로는 선형적이지 않은 상황을 마주할 가능성이 높음
✅ EX. 신용 한도(T)가 신용카드 소비(Y)에 미치는 인과 효과 추정

이 예제에서 상황을 간소화해서 유일한 교란 요인이 임금(wage)이라고 했을 때 (즉, 은행에서 T 결정 시 유일하게 wage정보만 사용한다고 할 때)

지금껏 배운 내용으로는 X(임금)을 통제하기 위해 T를 X에 회귀하여 잔차 T(~)를 구하여 T의 편향을 제거할 수 있다.
하지만, 조건부 X 하에서 T와 Y의 관계가 선형적이지 않다면, 문제가 생긴다.

- 처치 반응 곡선에는 오목성이 존재한다. 신용 한도(T)가 높을 수록 곡선의 기울기가 낮아짐
- 기울기와 인과효과는 밀접한 관련이 있다고 했었다.
- 인과 추론 관점에서 T가 증가함에 따라 T가 Y에 미치는 효과는 감소한다고 볼 수 있음
→ 즉, 한도를 2,000에서 3,000으로 늘렸을 때보다, 1,000에서 2,000으로 늘렸을 때 소비가 더 많이 증가하는 경향이 존재
4.6.1 처치 선형화
T를 Y와 선형관계로 변환하기 위해서 신용 한도(T)에 오목 함수 적용해보기
→ 로그 함수, 제곱근 함수 또는 T를 분수의 거듭제곱으로 취하는 함수 등 많은 방법이 후보가 될 수 있음

제곱근 함수를 사용해서 T에 오목 함수를 적용해보자
plt_df = (spend_data
# credit_limit(T)에 제곱근 취하기
.assign(credit_limit_sqrt = np.sqrt(spend_data["credit_limit"]))
.assign(wage_group = pd.IntervalIndex(pd.qcut(spend_data["wage"], 5)).mid)
.groupby(["wage_group", "credit_limit_sqrt"])
[["spend"]]
.mean()
.reset_index())
→ 이런 식으로 여러 함수를 시도해보고, 어떤 함수가 T를 가장 잘 선형화하는지 직접 확인해야 한다.

다음과 같은 모델을 추정하여 인과 매개변수 β1 찾기
model_spend = smf.ols(
'spend ~ np.sqrt(credit_limit)',data=spend_data
).fit()
model_spend.summary().tables[1]

하지만 교란(임금) 때문에, 임금이 높아지면 신용 한도(T)와 소비(Y)가 모두 증가하여 기울기가 상향 편향된 모습
교란요인(wage) 모델에 추가하기
model_spend = smf.ols('spend ~ np.sqrt(credit_limit)+wage',
data=spend_data).fit()
model_spend.summary().tables[1]
4.6.2 비선형 FWL과 편향 제거
비선형 데이터에 FWL 정리를 적용하기 위해서는, 먼저 비선형 처리를 해야 한다.
선형회귀분석을 이용해 비선형 모델 추정하기
1.처치 선형화 단계: T와 Y의 관계를 선형화하는 함수 F 찾기
debias_spend_model = smf.ols(f'np.sqrt(credit_limit) ~ wage',
data=spend_data).fit()
2. (FWL) 편향 제거 단계: F(T)를 교란 요인(X)에 회귀하고, 처치 잔차 F(T~) 구하기
denoise_spend_model = smf.ols(f'spend ~ wage', data=spend_data).fit() #잔차를 구하기 위한 모델 생성
credit_limit_sqrt_deb = (debias_spend_model.resid
+ np.sqrt(spend_data["credit_limit"]).mean())
3. (FWL) 잡음 제거 단계: 결과 Y를 교란 요인(X)에 회귀하고, 결과 잔차 Y(~) 구하기
spend_den = denoise_spend_model.resid + spend_data["spend"].mean()
4. (FWL) 결과 모델 단계: 결과 잔차 Y(~)를 처치 잔차 F(T~)에 회귀하여, F(T)가 Y에 미치는 인과효과의 추정값 구하기
# 기존 df spend_data에 구한 잔차 credit_limit_sqrt_deb와 spend_den 추가하기
spend_data_deb = (spend_data
.assign(credit_limit_sqrt_deb = credit_limit_sqrt_deb,
spend_den = spend_den))
final_model = smf.ols(f'spend_den ~ credit_limit_sqrt_deb',
data=spend_data_deb).fit()
final_model.summary().tables[1]

4.7 더미변수를 활용한 회귀분석
- 일부 공변량을 통제했을 때 처치가 무작위로 배정된 것처럼 보이도록 가정해야 하지만, 어려운 일이다.
- 모델에 모든 교란 요인이 포함되는지 판단하기는 매우 어렵기 때문
- 가능하면 무작위 실험을 하는 것이 좋으나, 큰 비용이 들 수 있음
4.7.1 조건부 무작위 실험
따라서 이상적인 무작위 통제 실험 대신, 차선책으로 계층화 또는 조건부 무작위 실험을 활용할 수 있다.
조건부 무작위 실험
: 공변량(X)에 따라 서로 다른 분포에서 표본을 뽑아 여러 국소 실험을 만드는 것
신용 한도(T)의 히스토그램(KDE)을 공통원인 위험도의 대리 변수 credit_score_buckets별로 표시해보자
plt.figure(figsize=(15,6))
sns.histplot(data=risk_data_rnd,
x="credit_limit",
hue="credit_score1_buckets",
kde=True,
palette="gray");
plt.title("Conditional random experiment")
- 신용 한도(T)가 서로 다른 분포에서 추출되었음을 알 수 있다.
- credit_score가 높은 고객(=저위험 고객,색이 진한 부분) 그룹은 히스토그램이 오른쪽으로 치우침(=왼쪽으로 꼬리가 김)
- 반대로 credit_score가 낮은 고객(=고위험 고객, 색이 연한 부분) 그룹은 히스토그램이 왼쪽으로 치우침(오른쪽으로 꼬리가 김)
* 베타 분포 샘플링: 이 실험에서는 신용 한도(T)를 베타 분포에서 추출했다. 베타 분포는 균등 분포의 일반화로 볼 수 있고, 샘플링(표본 추출)을 특정 범위로 제한하고 싶을 때 유용하다.
조건부 무작위 실험 설계 시 두 가지 경험적 규칙 적용하기
- 조건부 무작위 실험은 무작위 실험보다 비용이 저렴하지만, 훨씬 복잡하다. 가능한한 무작위 실험에 가깝게 설계할 것
- trade-off 존재, 두 가지 규칙을 만족할 수록 해석은 더 쉬워지지만, 더 큰 비용이 든다.
- 그룹 수가 적을 수록 조건부 무작위 실험을 진행하기 더 쉬워짐 - 예제에서는 공변량 1~1000까지 범위 중 credit_scroe1을 200단위로 나누어 그룹이 5개로 적게 유지함
- 그룹 간 처치 분포가 많이 중첩될수록 분석이 용이해짐 - 양수성 가정과 관련이 있는데, 예제에서는 고위험 그룹(C)이 높은 신용 한도(T)를 받을 확률이 0인 경우, 고위험 그룹이 높은 신용한도를 받게 된다면 어떤 일이 발생할지 알기 위해 위험한 외삽에 의존해야 한다.
* 계층화 실험: 분산을 최소화하고, 계층화된 변수에 대해 실험-대조군 사이의 균형을 보정하기 위한 방법 (신용카드 한도 예제에서는 모든 계층에서 처치 분포가 동일하도록 설계)
4.7.2 더미 변수
조건부 무작위 실험의 장단점
- 장점 - 조건부 독립 가정에 훨씬 더 설득력이 생긴다.
- 단점 - 실험군에 대한 결과만으로 단순 회귀분석을 하면, 편향된 추정값을 얻게 된다.
교란 요인을 포함하지 않고 모델 추정 시 결과는 다음과 같다.

model = smf.ols("default ~ credit_limit", data=risk_data_rnd).fit()
model.summary().tables[1]
→ 인과 추정량 β1 = -9.344e-06으로 음수이다.
- 더 높은 신용 한도가 고객의 채무 불이행 위험을 낮추지는 않으므로 말이 되지 않음
- 실험이 설계된 방식으로 인해, 위험도(credit_score_1) 가 낮은 고객이 평균적으로 더 높은 한도(T)를 받았기 때문에 음수가 나온 것
이를 보정하기 위해 모델에 처치가 무작위로 배정된 그룹 정보 포함시키기
→ 원-핫 인코딩으로 더미변수(가변수) 만들기
- 더미변수는 그룹에 대해 이진값으로 구성된 열 (속하면 1, 속하지 않으면 0)
- 여기에서는 대리변수 credit_score1_buckets를 통제
- pandas의 pd.get_dummies 함수 사용
risk_data_dummies = (risk_data_rnd
.join(pd.get_dummies(risk_data_rnd["credit_score1_buckets"],
prefix="sb",
drop_first=True)))
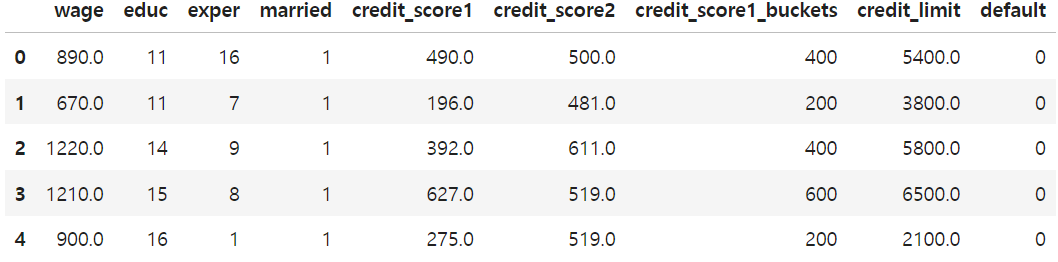
risk_data_dummies.head()
# statsmodels로 식에 C() 함수를 넣어 간단히 더미 변수를 만들 수 있다.
# model = smf.ols("default ~ credit_limit + C(credit_score1_buckets)",
# data=risk_data_rnd).fit()
대리 변수 credit_score1의 더미 변수를 포함시켜 β1 재추정
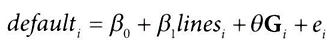
model = smf.ols(
"default ~ credit_limit + sb_200+sb_400+sb_600+sb_800+sb_1000",
data=risk_data_dummies
).fit()
model.summary().tables[1]
- 대리 변수의 그룹정보인 더미 변수 추가 후 처치(credit_limit)의 베타1 추정량이 제대로 양수가 나온 모습
- 기울기 매개변수(β1)는 하나이다.
- 교란 요인을 통제하려고 더미변수를 추가했을 때 절편은 그룹 당 하나씩 생기나, 모든 그룹에 동일한 기울기가 적용됨
- 해당 기울기는 각 그룹의 회귀에 대한 분산 가중평균이 됨
각 그룹의 모델 예측결과를 시각화해보면, 그룹별로 하나의 선이 있으나, 기울기가 모두 동일함을 알 수 있음

4.7.3 포화회귀모델
- 이 장 초반에 "회귀 분석과 조건부 평균은 비슷하다"라고 했었다.
- 즉, 이진 처치에 대한 회귀분석은 실험-대조군의 평균을 비교하는 것과 같음
- 더미변수는 이진값이므로, 같은 논리가 적용된다
조건부 무작위 실험 데이터를 credit_score1_buckets에 따라 나누고, 그룹별 효과 추정
def regress(df, t, y):
return smf.ols(f"{y}~{t}", data=df).fit().params[t]
effect_by_group = (risk_data_rnd
.groupby("credit_score1_buckets")
.apply(regress, y="default", t="credit_limit"))
effect_by_groupcredit_score1_buckets
0 -0.000071
200 0.000007
400 0.000005
600 0.000003
800 0.000002
1000 0.000000
dtype: float64
bucket별 크기를 가중치로 삼아 bucket별 효과를 가중평균 취해서 평균 효과 구하기
group_size = risk_data_rnd.groupby("credit_score1_buckets").size()
ate = (effect_by_group * group_size).sum() / group_size.sum()
ate
> 4.490445628748722e-06 ✅ 포화 모델(saturated model)
: 회귀분석에서 모든 가능한 설명변수와 그 상호작용을 포함하는 모델
- 주어진 데이터에 대해 모든 변수+상호작용을 포함하므로 과적합 위험이 있어 일반화 능력이 떨어질 수 있음
- 그러나 특정 그룹의 인과효과를 파악하는 데에 유용하게 쓰임
앞서 "그룹별 효과를 추정해서 가중평균을 낸 것"과 똑같은 작업을 회귀분석에서 수행하기
(↔ 더미변수와 처치에 대한 상호작용 항에서, 각 더미변수에 해당하는 그룹의 인과효과 추정하기)
model = smf.ols("default ~ credit_limit * C(credit_score1_buckets)",
data=risk_data_rnd).fit()
model.summary().tables[1]
첫 번째 더미변수를 제외했으므로 credit_limit과 관련된 매개변수는 생략된 더미 그룹 sb_100의 효과를 나타냄
(credit_limit의 매개변수 -7.072e-05는 credit_score1_buckets 그룹1(0~200)의 추정값과 동일)
# bucket의 첫 번째 더미변수 제외했었음
risk_data_dummies = (risk_data_rnd
.join(pd.get_dummies(risk_data_rnd["credit_score1_buckets"],
prefix="sb",
drop_first=True)))
상호작용 매개변수는 생략된 첫 번째 그룹의 효과와 연관지어 해석해야 한다.
→ credit_limit(T)과 관련된 매개변수 + 상호작용 항 = 회귀분석을 사용해 그룹별 추정된 효과를 얻을 수 있다.
(↔ 그룹별로 각각 추정된 효과와 동일)
(model.params[model.params.index.str.contains("credit_limit:")] #처치인 credt_limit과 상호작용하는 다른 변수들 파라미터 선택
+ model.params["credit_limit"]).round(9) # 선택된 상호작용 파라미터에 credit_limit 파라미터를 추가하여 총 효과 계산credit_limit:C(credit_score1_buckets)[T.200] 0.000007
credit_limit:C(credit_score1_buckets)[T.400] 0.000005
credit_limit:C(credit_score1_buckets)[T.600] 0.000003
credit_limit:C(credit_score1_buckets)[T.800] 0.000002
credit_limit:C(credit_score1_buckets)[T.1000] 0.000000
dtype: float64위의 효과 (T 매개변수 + T와의 상호작용 항)를 시각화하면, 그룹마다 별도의 회귀 모델을 적합시킨 것처럼 보인다.
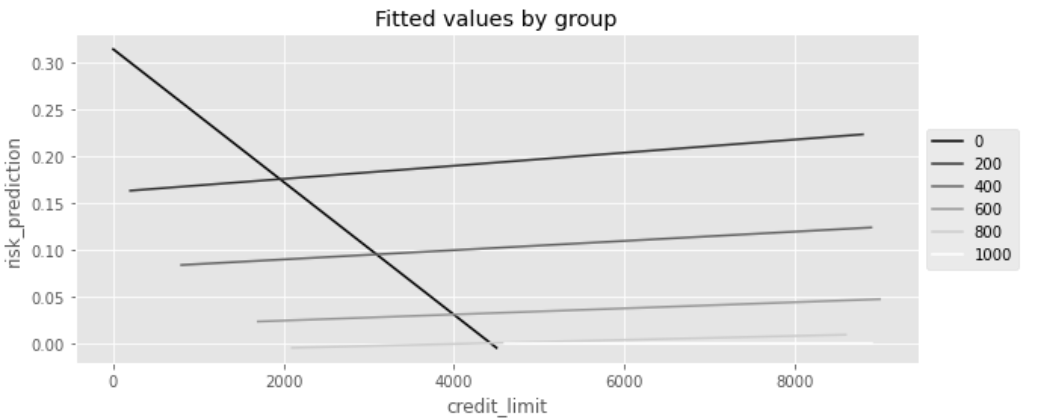
- 각 선은 절편뿐만 아니라, 기울기도 다름
- 또한, 매개변수(자유도)가 더 맞지 않음 (↔ 모든 조건이 동일할 때 분산이 더 큼)
- 맥락과 맞지 않는, 기울기가 음인 선이 나타남
- 이 기울기는 통계적으로 유의하지 않으며, 해당 그룹에서의 작은 표본 크기 때문에 발생한 잡음일 확률
4.7.4 분산의 가중평균과 회귀분석
4.7.3에서 '포화회귀모델'과 '그룹별 계산 결과'가 동일함을 확인하였다.
- 중요한 의문점
- 상호작용 항 없이 (default ~ credit_limit + C(credit_score1_buckets ) 모델을 실행하면 단일 효과 (=하나의 기울기 매개변수)만 얻게 됨
- 이 효과 추정값은 그룹별 효과를 추정하고 가중평균 낸 결과와 다르다는 점이 중요
- 즉, 회귀분석은 여러 그룹의 효과를 합친 것이지만, 표본 크기를 기준으로 한 가중평균은 아닌 것
- 그렇다면 무엇일까?
그 답을 알기 위해서 시뮬레이션 해볼 1번 그룹과 2번 그룹 생성

- 1번 그룹은 크기가 1,000이고 평균 처치효과가 1, 표준편차는 1
- 2번 그룹은 크기가 500이고 평균 처치효과가 2, 표준편차는 2
- 그룹 별 효과를 가중평균낸 결과 ATE는 ( 1 * 1000 + 2 * 500 / 1500 ) = 1.33이다.
그룹을 통제하면서(+C(g)) Y를 T에 회귀하면 다른 결과가 나타난다.
model = smf.ols("y ~ t + C(g)", data=df).fit()
model.paramsIntercept 0.024758
C(g)[T.2] 0.019860
t 1.625775
dtype: float64
→ 그룹2의 표본이 그룹1의 절반임에도, 결합한 효과는 그룹2의 효과에 더 가까움
→ 그 이유는, "회귀분석은 그룹 효과를 결합할 때 표본 크기를 가중치로 사용하는 대신에, 각 그룹에서 처치의 분산에 비례하는 가중치를 사용"하기 때문
- 회귀분석은 처치 변동성이 큰 그룹을 선호한다.
- 한 그룹 내에서 처치가 별로 변하지 않으면, 그 효과를 확신할 수 없을 것
- 처치가 많이 변할수록 결과에 미치는 영향이 더 분명해진다.
여러 그룹이 있고, 그룹 내 처치가 무작위 배정된 경우, 조건부 원칙(보정 공식)에 따른 효과는 각 그룹내 효과의 가중평균

회귀분석에서는 가중치로 '처치의 분산'을 사용하지만, 사용하는 방법에 따라 그룹의 표본 크기와 같이 다른 가중치를 직접적용해볼 수 있다.
4.7.5 평균 제거와 고정효과
- FWL 정리는 앞서 살펴본 모델에 더미변수를 포함시켜 그룹 간 다르게 처치 배정하는 방법과 같이 더미변수가 있는 상황에서 그 진가를 발휘한다.
- 더미변수 추가 시, 번거롭고 연산 과정이 복잡하며, 대부분 0이 많은 열이 생성된다는 단점이 있다.
- 여기에 FWL 정리를 적용하고, 회귀분석이 T를 직교화하는 방법을 이해하면 더 쉽게 해결 가능
FWL ⓛ 편향 제거 단계인 공변량(credit_score1_buckets)에서 처치(credit_limit)를 예측하는 과정 수행
*공변량(X)이 더미변수
model_deb = smf.ols("credit_limit ~ C(credit_score1_buckets)",
data=risk_data_rnd).fit()
model_deb.summary().tables[1]
- credit_score1_buckets=1이면 credit_score1_buckets=1 그룹의 평균 신용 한도 예측
- 1173.0769 (Intercept) + 2195.4337 (T.200의 coef) = 3368.510638
- 이 예측값은 각 그룹의 평균값
risk_data_rnd.groupby("credit_score1_buckets")["credit_limit"].mean()credit_score1_buckets
0 1173.076923
200 3368.510638
400 4575.456498
600 5364.400448
800 5812.587413
1000 6180.000000
Name: credit_limit, dtype: float64
→ group(T.200)의 값이 위의 예측값과 동일하게 3368.510638 이 나옴
더미변수 활용 시, 간단하게 처치를 잔차화할 수 있다.
1. 그룹별 평균 처치(credit_limit) 계산하기
risk_data_fe = risk_data_rnd.assign(
credit_limit_avg = lambda d: (d
.groupby("credit_score1_buckets")
["credit_limit"].transform("mean"))
)
2. 평균 제거(demeaning)
: 처치에서 해당 그룹의 평균을 빼서 잔차 구하기 → 회귀식에서 I(T-T_avg)를 사용해 demeaning 작업을 수행할 수 있다.
model = smf.ols("default ~ I(credit_limit-credit_limit_avg)",
data=risk_data_fe).fit()
model.summary().tables[1]
- 여기서 얻은 추정값은 모델에 더미변수를 추가해서 얻은 값과 동일하다.
- 이렇게 그룹 내에서 고정된 모든 것을 통제하여 얻은 모델을 '고정 효과 모델'이라고 하며,
- 고정된 것을 통제하는 수단(ex. 더미 변수)를 '고정 효과'라 한다.
또 다른 아이디어는 회귀 모델 안에 그룹별 평균 처치를 포함(+credit_limit_avg)시켜서, 회귀 분석을 통해 추가된 변수들로부터 처치를 잔차화하는 방법이 있다.
model = smf.ols("default ~ credit_limit + credit_limit_avg",
data=risk_data_fe).fit()
model.summary().tables[1]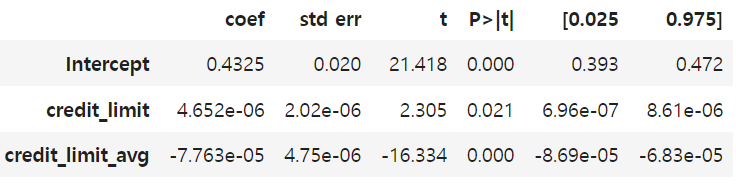
✅ EX. 마케팅 믹스 모델링(MMM, Marketing Mix Modeling)
: 광고를 볼 사람을 무작위로 선정할 수 없기에, 광고 업계에서 광고 효과 측정시 랜덤화의 대안으로 널리 사용하는 방법
- MMM은 마케팅 매출을 마케팅 전략 지표와 몇 가지 교란 요인에 회귀한 것에 불과함
- 예를 들어 TV와 SNS, 그리고 검색 광고 예산이 매출에 미치는 영향을 알고 싶다면, 각 실험 대상 i가 '하루'인 회귀분석을 실행하면 된다.

- δ0 : 기준 성과(=다른 모든 요인이 최소일 때의 성과)
- βi : 변수의 변화가 KPI(여기선 Sales)에 미치는 영향
- 효과가 좋은 달에 마케팅 예산을 늘렸을 수 있다는 점을 고려하여, 회귀 모델에 추가 통제변수를 포함해서 교란 요인을 보정할 수 있다.
- ex. 경쟁사의 매출, 각 월에 대한 더미 변수, 추세 변수등
4.7 누락 변수 편향
- 3장에서 공통 원인(교란 요인)이 처치와 결과 간의 추정 관계를 편향시킬 수 있다고 했었다.
- 회귀분석은 이러한 교란 편향에 대해 고유한 관점을 주고, 더 정확하게 다룰 수 있게 해줌
임금을 공통 원인(교란)으로 갖고 있는 상황에서,

다음과 같이 교란 요인을 포함하는 모델을 추정해야 하고,

포함하지 않고 교란 요인이 누락된 축소 모델을 추정하면 추정값은 편향될 것
short_model = smf.ols("default ~ credit_limit", data=risk_data).fit()
short_model.params["credit_limit"]
> -2.401961992596885e-05✅ 누락 변수 편향(OVB, omitted variable bias)
- β omitted : 누락 변수가 포함된 전체 모델의 회귀계수를 더하고, (결과Y~처치T+누락변수X)
- δ omitted : 결과에 미치는 누락 변수의 효과를 곱하고, (누락변수X~처치T)
- 누락 변수가 포함된 변수에 회귀하는 모델의 회귀계수라고 정의할 수 있다.

코드로 누락 변수 편향(OVB) 공식 구현하여 편향된 매개변수 추정값 확인하기
long_model = smf.ols("default ~ credit_limit + wage",
data=risk_data).fit()
omitted_model = smf.ols("wage ~ credit_limit", data=risk_data).fit()
(long_model.params["credit_limit"]
+ long_model.params["wage"]*omitted_model.params["credit_limit"])'
> -2.4019619925968762e-05
→ 앞서 교란 요인(wage)이 누락된 축소 모델을 추정하여 얻은 편향된 추정값과 동일한 값이 출력됨
4.9 중립 통제변수
- 이제껏 교란 요인 X를 보정하면서 처치 T가 Y에 미치는 영향을 알고 싶을 때에는
- 모델에 X를 포함하거나,
- X로 T를 예측한 후 잔차를 구하고, 이 잔차를 편향 제거된 처치로 사용해서 같은 결과를 얻는 방법을 배웠다.
- 그렇다면 X에 어떤 변수들을 포함해야 할까?
- 공통효과(충돌부)나 매개자는 선택편향을 유발할 수 있으므로 포함시키지 않는 것이 좋다.
- 무해해보이지만 실제로 해로울 수 있는 통제변수가 있다.
✅ 중립 통제변수
: 회귀분석 추정에서 편향에 영향을 미치지 않는다는 점에서 중립적이나, 분산에는 심각한 영향을 줄 수 있는 변수
* 회귀분석에 특정 변수를 포함할 때는 편향-분산 트레이드오프가 존재한다는 점을 명심할 것

다음과 같은 DAG를 고려해볼 때, 모델에 credit_score2를 포함해야할까?
formula = "default~credit_limit+C(credit_score1_buckets)+credit_score2"
model = smf.ols(formula, data=risk_data_rnd).fit()
model.summary().tables[1]
- credit_limit(T)의 매개변수 추정값이 조금 더 커졌다. ( ← 추가한 변수가 결과 Y를 잘 예측 )
- 표준오차가 감소하였다. ( ← 추가한 변수가 선형회귀의 잡음 제거 단계에 기여 )
→ FWL의 마지막 단계가 credit_score2를 포함하므로, Y(~)의 분산이 감소하고, 이를 T(~)에 회귀하면 더 정확한 결과를 얻을 수 있다.
→ 선형회귀분석에서 "결과를 예측할 수 있고 선택편향을 유발하지 않는 변수"를 포함시켜서 요인 보정 뿐만 아니라, 잡음을 줄이는 데도 사용할 수 있다.
(완전 무작위 배정된 A/B테스트 데이터와 같이 편향이 없는 경우에도 여전히 잡음을 줄이는 도구로 회귀분석을 활용할 수 있음)
* 잡음 제거 기법으로 FWL말고도 MS에서 개발한 CUPED를 사용할 수 있다.
4.9.1 잡음 유발 통제변수
- 통제변수는 잡음을 줄일 수도 있지만, 늘릴 수도 있다.
앞서 교란 요인이었던 credit_score1이 교란 요인이 아니라고 가정해보자.

credit_score1은 T의 원인이지만, Y의 원인이 아니기에, 공통원인이 아니고 보정할 필요가 없다.
단순회귀로 제곱근 함수를 적용하여 인과효과를 추정해보자
spend_data_rnd = pd.read_csv("data/spend_data_rnd.csv")
model = smf.ols("spend ~ np.sqrt(credit_limit)",
data=spend_data_rnd).fit()
model.summary().tables[1]
위의 결과를 교란 요인이 아닌 credit_score1_buckets를 포함시킨 결과 값과 비교
model = smf.ols("spend~np.sqrt(credit_limit)+C(credit_score1_buckets)",
data=spend_data_rnd).fit()
model.summary().tables[1]
- 표준오차가 증가하여 인과 매개변수의 신뢰구간이 넓어짐
- OLS는 처치의 분산이 큰 그룹을 선호하기 때문
- 그러나 T를 설명하는 공변량(교란요인)을 통제하면, 분산을 줄일 수 있을 것
4.9.2 특성 선택: 편향-분산 트레이드오프
- 현실적으로는 처치에만 영향을 주고 결과에는 영향을 주지 않는 공변량(X)을 찾아보기 어렵다.
강력한한 원인인지, 약한 원인인지 선의 굵기로 나타냈을때,

- X1은 T의 강력한 원인이지만, Y의 약한 원인
- X3은 Y의 강력한 원인이지만, T의 약한 원인
- X2는 X1과 X3의 중간 수준의 원인 (점선)
T의 원인인 공변량을 보정해야 편향이 제거된다. ↔ 하지만 보정하면 추정량의 분산이 증가한다.
- 모든 교란 요인을 통제하면서 효과를 추정하면, 추정값의 표준오차가 너무 크므로 제대로된 결론을 내릴 수 없음
- 교란 요인 중 하나가 T의 강력한 예측자이고, Y의 약한 예측자임을 알고 있다면, 모델에서 제외할 수 있다.(X1이 해당)
- 추정값이 편향될 수 있으나, 분산을 크게 줄인다면 지불할 가치가 있는 대가일 수도 있다.
→ T를 잘 설명하고, Y를 거의 설명하지 않는다면, 보정 대상에서 배제해야 한다.
4.10 요약
- 예측 도구가 아닌, 교란 요인 보정과 분산 감소 관점에서 회귀분석에 대해 배웠다.
- 조건부 독립성이 유지될 때, 직교화를 이용해 처치가 무작위로 배정된 것처럼 보이게 할 수 있다.
- 즉, T를 X에 회귀하여 편향 제거된 T인 잔차를 구하여 X로 인한 교란편향을 보정
- FWL 정리에 따른 다중회분석의 세 단계
- 편향 제거 단계에서 T(~)를 구하고,
- 잡음 제거 단계에서 Y(~)를 구하고,
- 결과 모델 단계에서 결과 잔차 Y(~)를 처치 잔차 T(~)에 회귀하여 T→Y의 인과효과 추정값을 구함
'데이터 분석 > 인과추론' 카테고리의 다른 글
| [5-2] 실무로 통하는 인과추론 with 파이썬 - 5장. 성향점수 (0) | 2024.05.18 |
|---|---|
| [5-1] 실무로 통하는 인과추론 with 파이썬 - 5장. 성향점수 (0) | 2024.05.14 |
| [4-1] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 (0) | 2024.05.09 |
| [3-2] 실무로 통하는 인과추론 with 파이썬 - 3장. 그래프 인과모델 (0) | 2024.05.05 |
| [3-1] 실무로 통하는 인과추론 with 파이썬 - 3장. 그래프 인과모델 (0) | 2024.05.01 |




