| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- tableau
- pmdarima
- lightgbm
- ImageDateGenerator
- ARIMA
- 부트 스트래핑
- Growth hacking
- 컨브넷
- 캐글 산탄데르 고객 만족 예측
- 스태킹 앙상블
- 인프런
- splitlines
- WITH ROLLUP
- 로그 변환
- 그룹 연산
- 마케팅 보다는 취준 강연 같다(?)
- WITH CUBE
- 데이터 증식
- 리프 중심 트리 분할
- DENSE_RANK()
- 3기가 마지막이라니..!
- 그로스 마케팅
- 데이터 핸들링
- 캐글 신용카드 사기 검출
- 그로스 해킹
- 분석 패널
- XGBoost
- sql
- 데이터 정합성
- python
- Today
- Total
LITTLE BY LITTLE
[3]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 - 훈련 프로세스 개선(고급최적화 기법 - 모멘텀, Ada군 / 정규화 기법 - 조기중단, L1&L2 정규화, 드롭아웃,배치 정규화 ) 본문
[3]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 - 훈련 프로세스 개선(고급최적화 기법 - 모멘텀, Ada군 / 정규화 기법 - 조기중단, L1&L2 정규화, 드롭아웃,배치 정규화 )
위나 2022. 9. 10. 22:50목차
1부. 컴퓨터 비전에 적용한 텐서플로2와 딥러닝
01. 컴퓨터 비전과 신경망02. 텐서플로 기초와 모델 훈련 (케라스, 텐서보드, 애드온, 확장, 라이트, TensorFlow.js, 모델 실행 장소)03. 현대 신경망 (다차원 데이터를 이용한 신경망, CNN작업, 유효수용영역, 훈련 프로세스 개선, 정규화 기법)
2부. 전통적 인식 문제를 해결하는 최신 솔루션
04. 유력한 분류 도구 (고급 CNN아키텍처의 이해 - VGG, GoogleLeNet, Inception,ResNet[잔차 네트워크], 전이학습)
05. 객체 탐지 모델 (YOLO, Faste R-CNN, 텐서플로 객체 탐지 API)
06. 이미지 보강 및 분할 (인코더-디코더로 이미지 변환, 노이즈 제거, 객체 분할)
3부. 컴퓨터 비전의 고급 개념 및 새 지평
07. 복합적이고 불충분한 데이터셋에서 훈련시키기 (입력 파이프라인, 데이터셋 보강, VAE와 GAN)
08. 동영상과 순환 신경망 (RNN, 장단기 메모리 셀, LSTM으로 동영상 분류하기)
09. 모델 최적화 및 모바일 기기 배포 (계산 및 디스크 용량 최적화, 온디바이스 머신러닝, MobileNet)
훈련 프로세스 개선
- 1장 컴퓨터 비전과 신경망에서 다뤘던 경사 하강 알고리즘의 단점을 해결하는 동시에 과적합을 피할 방법을 알아보자.
- 경사 하강법의 까다로운 점 : 학습률 초매개변수 값을 사용하면 훈련이 반복될 때마다 손실 경사에 따라 네트워크 매개변수가 업데이트 되는 방식을 강화시키거나 약화시킨다.
- 이러한 경사 하강법의 특징 때문에, 학습률을 신중하게 설정해야함
- 학습률을 신중하게 설정해야하는 이유 1 - 훈련속도와 트레이드 오프 : 학습률 높게 설정 => 훈련된 네트워크가 빠르게 수렴 (즉, 훈련이 반복될 때마다 매개변수가 크게 업데이트되므로 반복 횟수가 줄어듦)
- 이러한 경사 하강법의 특징 때문에, 학습률을 신중하게 설정해야함
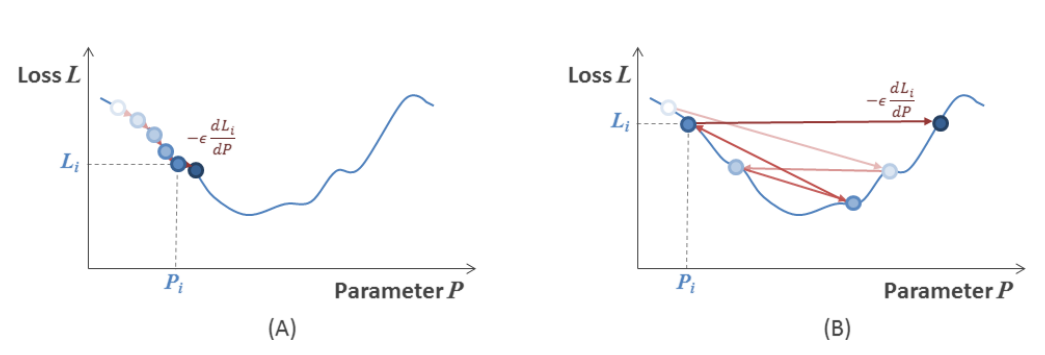
=> 학습률을 과도하게 낮게 잡으면 수렴하는 데까지 오래 걸림 (A)
=> 학습률을 과도하게 높게 잡으면 극솟값을 지나쳐버릴 수 있음 (B)
=> 훈련 시키는 동안 학습률을 동적으로 조정하는 방법 : 큰 값으로 시작해서 Epoch가 넘어갈 때마다 학습률을 감소시키기 ("학습률 감소"), 텐서플로에서는 "학습률 스케줄러", "적응형 학습률을 적용하는 최적화기" 제공
준최적 극솟값(Suboptimal local minima)

: 경사 하강법은 더 나은 최솟값이 가까이 있더라도, 벗어날 수 없는 극솟값으로 귀결될 수 있다.
- SGB 경사하강법은 훈련 샘플을 랜덤 샘플링하기 대문에, (즉, 경사가 종종 미니배치마다 달라서) 얕은 극솟갑에서 벗어날 수 있음
- 경사 하강 프로세스를 사용한다고 최솟값으로 수렴한다는 보장은 없음 (즉, 가능한 모든 조합 중 최선의 매개변수 집합으로 수렴한다는 보장은 없음)
- 따라서 주어진 최솟값이 실제로 최선인지 확인하기 위해 전체 손실 도메인을 스캔해야함
이기종 매개변수를 위한 단일 초매개변수
- 전통적 경사 하강법에서는 동일한 학습률이 네트워크의 모든 매개변수를 업데이트하는 데 사용됨
- 모든 변수가 변화에 동일한 민감도를 갖지 않으며, 반복할 때마다 모든 변수가 손실에 영향을 주지도 않음
- 결정적 매개변수를 하위집합 단위로하여 학습률을 다르게 적용, 네트워크 예측에 충분히 기여하지 않는 매개변수는 과감하게 업데이트하기
고급 최적화 기법 (모멘텀 알고리즘, 네스테로프 가속 경사, Ada군)
- SGD를 기반으로 만들어진 최적화 알고리즘
- 모멘텀 알고리즘
- 네트워크가 손실 최솟값에 실제로 가까이 다가갈 때, 누적 모멘텀이 너무 높아 메소드가 타겟 최솟값을 놓치거나, 그 주변을 왔다갔다할 수 있음
- 모멘텀은 SGD의 선택 매개변수로 정의된다.
- 모멘텀 알고리즘
import tensorflow as tf
optimizer = tf.optimizers.SGD(lr=0.01, momentum=0.9, # 'momentum' = "mu"
decay = 0.0, nesterov=False)모멘텀 알고리즘 - 간단한 훈련단계
@tf.function
def train_step(batch_images, batch_gts): # 전형적인 훈련 단계
with tf.GradientTape() as grad_tape: # TF에 경사를 기록할 것을 지시
batch_preds = model(batch_images, training=True) # 전방 전달
loss = tf.losses.MSE(batch_gts, batch_preds) # 손실 계산
# 손실 경사 w.r.t 훈련 가능한 매개변수를 취해 역전파
grads = grad_tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
2. 네스테로프 가속 경사(NAG, Nesterov accelerated gradient, 네스테로프 모멘텀) : 경사 변화에 좀 더 적응해 경사 하강 프로세스의 속도를 상당히 높일 수 있음
3. Ada군 (Adagrad, Adadelta, Adam)
- Adagrad, Adadelta, Adam 등은 민감도 및 활성화 빈도에 따라 학습률을 조정하는 아이디어에 몇 가지 반복과 변형을 준 알고리즘
- Adagrad
- 일반적으로 발견되는 특징과 연결된 매개변수에 대해서는 자동으로 학습률을 더 빠르게 감소시킴
- 드물게 발견되는 특징은 더 천천히 감소시킴
- Adadelta
- Adagrad는 반복할 때마다 학습률을 계속 감소시켜서, 어느 시점에는 학습률이 너무 작아 네트워크가 더이상 학습 X => 매개변수마다 학습률을 나누기 위해 사용되는 요인을 지속적으로 확인함으로써 이 문제를 방지함
- RMSprop과 유사함
- Adam (Adaptive moment estimation)
- 매개변수마다 학습률을 조정하기 위해 이전 업데이트 항을 저장할 뿐만 아니라, 과거 모멘텀 값을 기록
- Adadelta와 모멘텀의 혼합형
- Adagrad
구현 ( Experimenting with Advanced Optimizers )
%matplotlib inline
import tensorflow as tf
import numpy as np
import matplotlib
from matplotlib import pyplot as plt데이터 준비
# 데이터 준비 - MNIST 데이터
num_classes = 10
img_rows, img_cols, img_ch = 28, 28, 1
input_shape = (img_rows, img_cols, img_ch)
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
x_train = x_train.reshape(x_train.shape[0], *input_shape)
x_test = x_test.reshape(x_test.shape[0], *input_shape)
print('Training data: {}'.format(x_train.shape))
print('Testing data: {}'.format(x_test.shape))모델 정의
# 모델 준비 - 르넷-5 모델, tf.keras.Sequential 사용
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten, Conv2D, MaxPooling2D
def lenet(name='lenet'):
model = Sequential(name=name)
# 1st block:
model.add(Conv2D(6, kernel_size=(5,5), padding='same', activation='relu', input_shape=input_shape))
# 2nd block:
model.add(Conv2D(16, kernel_size=(5,5), activation='relu'))
model.add(MaxPooling2D(pool_size=(2,2)))
# Dense layers:
model.add(Flatten())
model.add(Dense(120, activation='relu'))
model.add(Dense(84, activation='relu'))
model.add(Dense(num_classes, activation='softmax'))
return model훈련
# 다양한 옵티마이저로 훈련시키기
from tensorflow.keras import optimizers
# Setting some variables to format the logs:
log_begin_red, log_begin_blue, log_begin_green = '\033[91m', '\n\033[94m', '\033[92m'
log_begin_bold, log_begin_underline = '\033[1m', '\033[4m'
log_end_format = '\033[0m'경사하강법, 모멘텀, NAG, Adagrad, Adadelta, rmsprop, Adam 성능 비교
optimizers_examples = {
'sgd' : optimizers.SGD(),
'momentum' : optimizers.SGD(momentum=0.9),
'nag' : optimizers.SGD(momentum=0.9, nesterov=True),
'adagrad' : optimizers.Adagrad(),
'adadelta' : optimizers.Adadelta(),
'rmsprop' : optimizers.RMSprop(),
'adam' : optimizers.Adam()
}훈련시키기
history_per_optimizer = dict()
print("Experiment: {0}start{1} (training logs = off)".format(log_begin_red, log_end_format))
for optimizer_name in optimizers_examples:
# 시드 리셋
tf.random.set_seed(42)
np.random.seed(42)
# Creating the model:
model = lenet("lenet_{}".format(optimizer_name))
optimizer = optimizers_examples[optimizer_name]
model.compile(optimizer=optimizer, loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# 훈련 시작
print("\t> Training with {0}: {1}start{2}".format(
optimizer_name, log_begin_red, log_end_format))
history = model.fit(x_train, y_train,
batch_size=32, epochs=20, validation_data=(x_test, y_test),
verbose=0)
history_per_optimizer[optimizer_name] = history
print('\t> Training with {0}: {1}done{2}.'.format(
optimizer_name, log_begin_green, log_end_format))
print("Experiment: {0}done{1}".format(log_begin_green, log_end_format))그래프 그리기
# plot the losses + accuracies
fig, ax = plt.subplots(2,2,figsize=(10,10), sharex='col')
ax[0,0].set_title("loss")
ax[0,1].set_title("val-loss")
ax[1,0].set_title("accuracy")
ax[1,1].set_title("val-accuracy")
lines, labels = [], []
for optimizer_name in history_per_optimizer:
history = history_per_optimizer[optimizer_name]
ax[0,0].plot(history.history['loss'])
ax[0,1].plot(history.history['val_loss'])
ax[1,0].plot(history.history['val_accuracy'])
line = ax[1,1].plot(history.history['val_accuracy'])
lines.append(line[0])
labels.append(optimizer_name)
fig.legend(lines, labels, loc='center right', borderaxespad=0.1)
plt.subplots_adjust(right=0.85)[Out]

정규화 기법 (조기중단, L1&L2 정규화, 드롭아웃, 배치정규화)
- 신경망을 효율적으로 가르쳐 훈련 데이터에서 손실을 최소화하는 것만으로는 충분하지 않음. 네트워크를 새로운 이미지에 적용했을 때에도 잘 수행되어야함 (=훈련 집합에 과적합되지 않아야함)
- 네트워크 일반화의 핵심은 "풍부한 훈련 집합"과 "잘 정의된 아키텍처",이와 별개로 최적화 단계를 정교화하는 정규화 프로세스에 대해 알아보자.
- 조기 중단
- 동일한 작은 훈련 샘플 집합에 대해 너무 여러번 반복할시 과적합되기 시작하기에, 모델에서 필요한 "적절한 훈련 세대수"를 알아야 한다.
- 훈련 세대 수는 네트워크가 과적합되기 시작하기 전에 종료시킬 수 있을 만큼 충분히 낮아야하지만, 훈련 집합에서 모든 것을 배울 수 있을만큼은 높아야 한다.
- 훈련과정이 중단될 때를 검증하는데 있어 핵심은 "교차 검증"이다. - '검증' 데이터셋을 최적화함으로써 훈련을 계속해야 할지, 중단해야 할지(=조기 중단) 측정
- 훈련 반복시 검증 손실과 metric을 모니터링하고,그래플르 그리고, 최적의 수준에서 저장된 가중치를 복원하는 모든 과정을 케라스의 '콜백(tf.keras.callbacks.EarlyStop)에서 자동으로 처리한다.
- L2, L2 정규화
- L1 정규화 (=LASSO 라쏘 정규화, Least Absolute Shrinkage and Selection Operator)
- 네트워크가 덜 중요한 특징에 연결된 매개변수를 0으로 축소
- 네트워크가 매개변수의 절댓값의 합을 최소화시키도록 함
- 큰 값을 갖는 가중치가 제곱으로 인해, 패널티를 부여받지 않는 대신 '네트워크가 덜 중요한 특징에 연결된 매개변수를 0으로 축소한다' => 덜 중요한 특징을 무시함으로써 과적합을 방지한다.
- 다른 말로, L1정규화는 네트워크가 희소 매개변수를 취하게 한다. 즉, 더 적은 수의 NULL값이 아닌 매개변수에 의존
- => 네트워크의 용량이 최소화되어야 하는 경우(ex.모바일 애플리케이션) 유리할 수 있다.
- L2 정규화 (=Ridge Regularization)
- 네트워크가 예측에 영향을 미치는 큰 값을 갖는 적은 수의 매개변수가 개발되는 것을 방지함
- 네트워크가 매개변수 값의 제곱의 합을 최소화하도록 강제
- 정규화로 인해 최적화 프로세스에서 모든 매개변수 값이 소멸되지만, 제곱 항으로 인해 매개변수는 더 강력하게 처벌됨(패널티)
- 매개변수 값을 낮게 유지해 더 균일하게 분산되게 하는 것
- => 네트워크가 예측에 영향을 미치는 큰 값을 갖는 적은 수의 매개변수가 개발되는 것을 방지한다. (네트워크가 일반화되는 것을 방지)
- L1 정규화 (=LASSO 라쏘 정규화, Least Absolute Shrinkage and Selection Operator)
- 드롭 아웃
- 훈련이 반복될 때마다 타겟 계층의 일부 뉴런의 연결을 임의로 끊음
- 초매개변수로 훈련단계마다 뉴런이 꺼질 확률을 나타내는 비율(0.1에서0.5 사이의 값으로 설정)을 취함
- 조기 중단
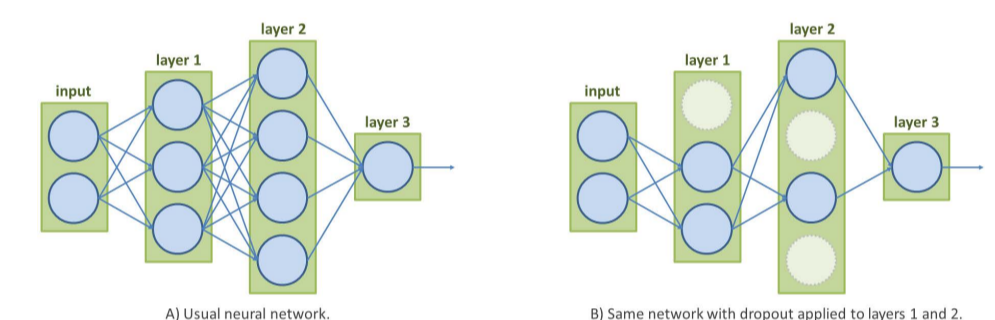
4. 배치 정규화
- 모델이 epoch마다 달라져도, 학습가능하도록 견고한 공동의 특징을 학습할 수 있게 해줌
- 드롭아웃이 핵심 특징을 담당하는 뉴런을 비활성화할 수 있으므로 네트워크는 동일한 예측에 도달하기 위해 다른 중요한 특징을 알아내야함 => 예측을 위해 데이터의 중복 표현(다른 특징으로도 예측가능한)을 개발하는 효과가 있음
- 수많은 모델을 동시에 훈련시키는 값싼 솔루션 (*훈련할 때에만 드롭아웃이 적용된다는 점 주의, 테스트시에는 전체 뉴런 다 씀)
- 네트워크의 예측은 부분적인 모델이 제공하는 결과의 조합으로 볼 수 있다.
구현 ( Applying Regularization Methods to CNNs )
import tensorflow as tf
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
import os
# Choosing which GPU this notebook can access
# (useful when running multiple experiments in parallel, on different GPUs):
os.environ["CUDA_VISIBLE_DEVICES"]= "1"
# 시드 설정:
random_seed = 42
# Setting some variables to format the logs:
log_begin_red, log_begin_blue, log_begin_green = '\033[91m', '\033[94m', '\033[92m'
log_begin_bold, log_begin_underline = '\033[1m', '\033[4m'
log_end_format = '\033[0m'# MNIST 데이터
num_classes = 10
img_rows, img_cols, img_ch = 28, 28, 1
input_shape = (img_rows, img_cols, img_ch)
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
x_train = x_train.reshape(x_train.shape[0], *input_shape)
x_test = x_test.reshape(x_test.shape[0], *input_shape)# Regularization의 효과를 더 잘 보기위해서 샘플 개수 줄이기
x_train, y_train = x_train[:200], y_train[:200] # ... 200 training samples instead of 60,000...
print('Training data: {}'.format(x_train.shape))
print('Testing data: {}'.format(x_test.shape))[Out]
Training data: (200, 28, 28, 1)
Testing data: (10000, 28, 28, 1)# 정규화 이용해서 훈련시키기
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.layers import (Input, Activation, Dense, Flatten, Conv2D,
MaxPooling2D, Dropout, BatchNormalization)
epochs = 200
batch_size = 32*참고 (Done manually)
@tf.function
def conv_layer(x, kernels, bias, s):
z = tf.nn.conv2d(x, kernels, strides=[1,s,s,1], padding='VALID')
# Finally, applying the bias and activation function (e.g. ReLU):
return tf.nn.relu(z + bias)
class SimpleConvolutionLayer(tf.keras.layers.Layer):
def __init__(self, num_kernels=32, kernel_size=(3, 3), stride=1):
""" Initialize the layer.
:param num_kernels: Number of kernels for the convolution
:param kernel_size: Kernel size (H x W)
:param stride: Vertical/horizontal stride
"""
super().__init__()
self.num_kernels = num_kernels
self.kernel_size = kernel_size
self.stride = stride
def build(self, input_shape):
""" Build the layer, initializing its parameters.
This will be internally called the 1st time the layer is used.
:param input_shape: Input shape for the layer (e.g. BxHxWxC)
"""
num_input_ch = input_shape[-1] # assuming shape format BHWC
# Now we know the shape of the kernel tensor we need:
kernels_shape = (*self.kernel_size, num_input_ch, self.num_kernels)
# We initialize the filter values e.g. from a Glorot distribution:
glorot_init = tf.initializers.GlorotUniform()
self.kernels = self.add_weight( # method to add Variables to layer
name='kernels', shape=kernels_shape, initializer=glorot_init,
trainable=True) # and we make it trainable.
# Same for the bias variable (e.g. from a normal distribution):
self.bias = self.add_weight(
name='bias', shape=(self.num_kernels,),
initializer='random_normal', trainable=True)
def call(self, inputs):
""" Call the layer, apply its operations to the input tensor."""
return conv_layer(inputs, self.kernels, self.bias, self.stride)
def get_config(self):
"""
Helper function to define the layer and its parameters.
:return: Dictionary containing the layer's configuration
"""
return {'num_kernels': self.num_kernels,
'kernel_size': self.kernel_size,
'strides': self.strides,
'use_bias': self.use_bias}When instantiating this layer, the regularizer passed as attributes will be attached to the layer.
The loss values of these regularizers can be obtained whenever, simply calling the layer's property .losses . Let us check:
from functools import partial
def l2_reg(coef=1e-2):
"""
Returns a function computing a weighed L2 norm of a given tensor.
(this is basically a reimplementation of f.keras.regularizers.l2())
:param coef: Weight for the norm
:return: Loss function
"""
return lambda x: tf.reduce_sum(x ** 2) * coef
class ConvWithRegularizers(SimpleConvolutionLayer):
def __init__(self, num_kernels=32, kernel_size=(3, 3), stride=1,
kernel_regularizer=l2_reg(), bias_regularizer=None):
"""
Initialize the layer.
:param num_kernels: Number of kernels for the convolution
:param kernel_size: Kernel size (H x W)
:param stride: Vertical/horizontal stride
:param kernel_regularizer: (opt.) Regularization loss for the kernel variable
:param bias_regularizer: (opt.) Regularization loss for the bias variable
"""
super().__init__(num_kernels, kernel_size, stride)
self.kernel_regularizer = kernel_regularizer
self.bias_regularizer = bias_regularizer
def build(self, input_shape):
"""
Build the layer, initializing its components.
"""
super().build(input_shape)
# Attaching the regularization losses to the variables.
if self.kernel_regularizer is not None:
self.add_loss(partial(self.kernel_regularizer, self.kernels))
if self.bias_regularizer is not None:
self.add_loss(partial(self.bias_regularizer, self.bias)conv = ConvWithRegularizers(num_kernels=32, kernel_size=(3, 3), stride=1,
kernel_regularizer=l2_reg(1.), bias_regularizer=l2_reg(1.))
conv.build(input_shape=tf.TensorShape((None, 28, 28, 1)))
# Fetching the layer's losses:
reg_losses = conv.losses
print('Regularization losses over kernel and bias parameters: {}'.format(
[loss.numpy() for loss in reg_losses]))
# Comparing with the L2 norms of its kernel and bias tensors:
kernel_norm, bias_norm = tf.reduce_sum(conv.kernels ** 2).numpy(), tf.reduce_sum(conv.bias ** 2).numpy()
print('L2 norms of kernel and bias parameters: {}'.format([kernel_norm, bias_norm]))[Out]
Regularization losses over kernel and bias parameters:
[2.0280523, 0.11339313] L2 norms of kernel and bias parameters: [2.0280523, 0.11339313]
model = Sequential([
Input(shape=input_shape),
ConvWithRegularizers(kernel_regularizer=l2_reg(1.), bias_regularizer=l2_reg(1.)),
ConvWithRegularizers(kernel_regularizer=l2_reg(1.), bias_regularizer=l2_reg(1.)),
ConvWithRegularizers(kernel_regularizer=l2_reg(1.), bias_regularizer=l2_reg(1.))
])
print('Losses attached to the model and its layers:\n\r{} ({} losses)'.format(
[loss.numpy() for loss in model.losses], len(model.losses)))Let us now build a LeNet-5 with our custom layers, and train it taking into account the regularization terms:
class LeNet5(Model): # `Model` has the same API as `Layer` + extends it
def __init__(self, num_classes,
kernel_regularizer=l2_reg(), bias_regularizer=l2_reg()):
# Create the model and its layers:
super(LeNet5, self).__init__()
self.conv1 = ConvWithRegularizers(
6, kernel_size=(5, 5),
kernel_regularizer=kernel_regularizer, bias_regularizer=bias_regularizer)
self.conv2 = ConvWithRegularizers(
16, kernel_size=(5, 5),
kernel_regularizer=kernel_regularizer, bias_regularizer=bias_regularizer)
self.max_pool = MaxPooling2D(pool_size=(2, 2))
self.flatten = Flatten()
self.dense1 = Dense(120, activation='relu')
self.dense2 = Dense(84, activation='relu')
self.dense3 = Dense(num_classes, activation='softmax')
def call(self, x): # Apply the layers in order to process the inputs
x = self.max_pool(self.conv1(x)) # 1st block
x = self.max_pool(self.conv2(x)) # 2nd block
x = self.flatten(x)
x = self.dense3(self.dense2(self.dense1(x))) # dense layers
return xoptimizer = tf.optimizers.SGD()
dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(batch_size)
log_string_template = 'Epoch {0:3}/{1}: main loss = {5}{2:5.3f}{6}; ' + \
'reg loss = {5}{3:5.3f}{6}; val acc = {5}{4:5.3f}%{6}'
def train_classifier_on_mnist(model, log_frequency=10):
avg_main_loss = tf.keras.metrics.Mean(name='avg_main_loss', dtype=tf.float32)
avg_reg_loss = tf.keras.metrics.Mean(name='avg_reg_loss', dtype=tf.float32)
print("Training: {}start{}".format(log_begin_red, log_end_format))
for epoch in range(epochs):
for (batch_images, batch_gts) in dataset: # For each batch of this epoch
with tf.GradientTape() as grad_tape: # Tell TF to tape the gradients
y = model(batch_images) # Feed forward
main_loss = tf.losses.sparse_categorical_crossentropy(
batch_gts, y) # Compute loss
reg_loss = sum(model.losses) # List and add other losses
loss = main_loss + reg_loss
# Get the gradients of combined losses and back-propagate:
grads = grad_tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# Keep track of losses for display:
avg_main_loss.update_state(main_loss)
avg_reg_loss.update_state(reg_loss)
if epoch % log_frequency == 0 or epoch == (epochs - 1): # Log some metrics
# Validate, computing the accuracy on test data:
acc = tf.reduce_mean(tf.metrics.sparse_categorical_accuracy(
tf.constant(y_test), model(x_test))).numpy() * 100
main_loss = avg_main_loss.result()
reg_loss = avg_reg_loss.result()
print(log_string_template.format(
epoch, epochs, main_loss, reg_loss, acc, log_begin_blue, log_end_format))
avg_main_loss.reset_states()
avg_reg_loss.reset_states()
print("Training: {}end{}".format(log_begin_green, log_end_format))
return model
model = LeNet5(10, kernel_regularizer=l2_reg(), bias_regularizer=l2_reg())
model = train_classifier_on_mnist(model, log_frequency=10)model = LeNet5(10, kernel_regularizer=None, bias_regularizer=None)
model = train_classifier_on_mnist(model, log_frequency=50)- A ~1% accuracy gain on the test set, which is non negligeable!
- The usage of add_loss() and .losses is however the main take-away of this experiment, as they can become useful for more complex models, when we want to apply layer-specific losses for instance.
- When it comes to regularization, TensorFlow and Keras already provide simpler tools, as we will cover in the next section.
Create Another Lenet-5 Model
Lenet-5
1. param name : Name for the model
2. param input_shape : Model's input shape
3. param use_dropout : Flag to add Dropout layers after key layers
4. param use_batchnorm : Flag to add BatchNormalization layers after key layers
5. param regularizer : Regularization function to be applied to layers' kernels
6. Return : LeNet-5 Keras model
# create another LeNet-5 factory function (using the Sequential API this time. just to illustrate the differences):
def lenet(name='lenet', input_shape=input_shape,
use_dropout=False, use_batchnorm=False, regularizer=None):
layers = []
# 1st block:
layers += [Conv2D(6, kernel_size=(5, 5), padding='same',
input_shape=input_shape, kernel_regularizer=regularizer)]
if use_batchnorm:
layers += [BatchNormalization()]
layers += [Activation('relu'),
MaxPooling2D(pool_size=(2, 2))]
if use_dropout:
layers += [Dropout(0.25)]
# 2nd block:
layers += [
Conv2D(16, kernel_size=(5, 5), kernel_regularizer=regularizer)]
if use_batchnorm:
layers += [BatchNormalization()]
layers += [Activation('relu'),
MaxPooling2D(pool_size=(2, 2))]
if use_dropout:
layers += [Dropout(0.25)]
# Dense layers:
layers += [Flatten()]
layers += [Dense(120, kernel_regularizer=regularizer)]
if use_batchnorm:
layers += [BatchNormalization()]
layers += [Activation('relu')]
if use_dropout:
layers += [Dropout(0.25)]
layers += [Dense(84, kernel_regularizer=regularizer)]
layers += [Activation('relu')]
layers += [Dense(num_classes, activation='softmax')]
model = Sequential(layers, name=name)
return modelL1정규화, L2정규화, 드롭아웃, 배치정규화, L1+배치정규화, L1+드롭아웃, L1+드롭아웃+배치정규화 성능 비교
configurations = {
'none' : {'use_dropout' : False, 'use_batchnorm' : False, 'regularizer' : None},
'L1' : {'use_dropout' : False, 'use_batchnorm' : False, 'regularizer' : tf.keras.regularizers.L1(0.01)},
'L2' : {'use_dropout' : False, 'use_batchnorm' : False, 'regularizer' : tf.keras.regularizers.L2(0.01)},
'dropout' : {'use_dropout' : True, 'use_batchnorm' : False, 'regularizer' : None},
'bn' : {'use_dropout' : False, 'use_batchnorm' : True, 'regularizer' : None},
'L1bn' : {'use_dropout' : False, 'use_batchnorm' : True, 'regularizer' : tf.keras.regularizers.L1(0.01)},
'L1dropout' : {'use_dropout' : True, 'use_batchnorm' : False, 'regularizer' : tf.keras.regularizers.L1(0.01)},
'L1dropoutbn' : {'use_dropout' : True, 'use_batchnorm' : True, 'regularizer' : tf.keras.regularizers.L1(0.01)}
}# 훈련시키기
history_per_instance = dict()
print("Experiment: {0}start{1} (training logs = off)".format(log_begin_red, log_end_format))
for config_name in configurations:
# 시드 리셋:
tf.random.set_seed(random_seed)
np.random.seed(random_seed)
# Creating the model:
model = lenet("lenet_{}".format(config_name), **configurations[config_name])
model.compile(optimizer='sgd', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# 훈련 시작:
print("\t> Training with {0}: {1}start{2}".format(
config_name, log_begin_red, log_end_format))
history = model.fit(x_train, y_train,
batch_size=32, epochs=30, validation_data=(x_test, y_test),
verbose=0)
history_per_instance[config_name] = history
print('\t> Training with {0}: {1}done{2}.'.format(
config_name, log_begin_green, log_end_format))
print("Experiment: {0}done{1}".format(log_begin_green, log_end_format))그래프 그리기
fig, ax = plt.subplots(2, 2, figsize=(10,10), sharex='col') # 직접적인 비교를 위해 add parameter `sharey='row'`
ax[0, 0].set_title("loss")
ax[0, 1].set_title("val-loss")
ax[1, 0].set_title("accuracy")
ax[1, 1].set_title("val-accuracy")
lines, labels = [], []
for config_name in history_per_instance:
history = history_per_instance[config_name]
ax[0, 0].plot(history.history['loss'])
ax[0, 1].plot(history.history['val_loss'])
ax[1, 0].plot(history.history['accuracy'])
line = ax[1, 1].plot(history.history['val_accuracy'])
lines.append(line[0])
labels.append(config_name)
fig.legend(lines,labels, loc='center right', borderaxespad=0.1)
plt.subplots_adjust(right=0.84)[Out]

for config_name in history_per_instance:
best_val_acc = max(history_per_instance[config_name].history['val_accuracy']) * 100
print('Max val-accuracy for model "{}": {:2.2f}%'.format(config_name, best_val_acc))[Out]
Max val-accuracy for model "none": 69.05%
Max val-accuracy for model "l1": 59.55%
Max val-accuracy for model "l2": 68.11%
Max val-accuracy for model "dropout": 48.69%
Max val-accuracy for model "bn": 78.85%
Max val-accuracy for model "l1+dropout": 79.03%
Max val-accuracy for model "l1+bn": 79.03%
Max val-accuracy for model "l1+dropout+bn": 79.00%
'4-2 > 이미지 딥러닝' 카테고리의 다른 글
| [6]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 - 객체 탐지 모델2 ( Faster R-CNN 이어서) (0) | 2022.10.03 |
|---|---|
| [5-1]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 - 객체 탐지 모델( YOLO, Faster R-CNN) (0) | 2022.09.23 |
| [4]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 - 유력한 분류 도구( VGG, GoogLeNet, 인셉션, ResNet, 전이학습) (1) | 2022.09.16 |
| [2]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 (CNN작업, 유효수용영역, 풀링계층, Lenet-5 구현) (0) | 2022.09.09 |
| [1]실전! 텐서플로2를 활용한 딥러닝 컴퓨터비전 (1장.컴퓨터 비전, 신경망 시작하기) (0) | 2022.09.07 |





