| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- 컨브넷
- 캐글 산탄데르 고객 만족 예측
- WITH ROLLUP
- Growth hacking
- lightgbm
- 인프런
- 데이터 핸들링
- 그로스 해킹
- python
- splitlines
- 데이터 증식
- 그룹 연산
- 마케팅 보다는 취준 강연 같다(?)
- tableau
- 분석 패널
- ARIMA
- sql
- XGBoost
- 부트 스트래핑
- 스태킹 앙상블
- 로그 변환
- 리프 중심 트리 분할
- 3기가 마지막이라니..!
- pmdarima
- 데이터 정합성
- ImageDateGenerator
- DENSE_RANK()
- 그로스 마케팅
- 캐글 신용카드 사기 검출
- WITH CUBE
- Today
- Total
LITTLE BY LITTLE
[3-1] 실무로 통하는 인과추론 with 파이썬 - 3장. 그래프 인과모델 본문

목차
<3장. 그래프 인과모델>
3.1 인과관계에 대해 생각해보기
3.1.1 인과관계 시각화
3.1.2 컨설턴트 영입 여부 결정하기
3.2 그래프 모델 집중 훈련
3.2.1 사슬 구조
3.2.2 분기 구조
3.2.3 충돌부 구조
3.2.4 연관성 흐름 치트 시트
3.2.5 파이썬에서 그래프 쿼리하기
3.3 식별 재해석
3.4 조건부 독립성 가정과 보정 공식
3.5 양수성 가정
3.6 구체적인 식별 예제
3.7 교란 편향
3.7.1 대리 교란 요인
3.7.2 랜덤화 재해석
3.8 선택 편향
3.8.1 충돌부 조건부 설정
3.8.2 선택편향 보정
3.8.3 매개자 조건부 설정
3.9 요약
3장에서는, 인과추론의 두 단계인 '식별'과 '추정' 중 더 어려운 식별 부분을 더 자세히 다룬다. 데이터로 매개변수를 추정하기 전 그래프 모델에 대한 이론적인 내용이다.
1. 기존 파이썬 라이브러리를 활용하여 그래프를 쿼리하고,
2. 그래프 모델을 통해서 식별의 개념을 재해석하며,
3. 식별을 방해하는 편향의 두 가지 원인과 인과 그래프 구조를 바탕으로 할 수 있는 것들에 대해 배운다.
3.1 인과관계에 대해 생각해보기
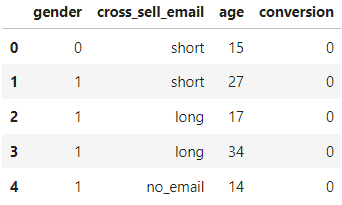
→ 데이터만 보고 독립성 가정 성립 여부를 판단할 수 없다.
→ 실험 대상에게 처치 배정에 관한 메커니즘 정보가 있어야 독립성 가정이 유지된다. (이 예제에서는 무작위로 발송되었다고 가정하였기에 독립성 가정 성립)
3.1.1 인과관계 시각화
- 교차 판매 이메일이 전환을 유도
- 관측된 다른 변수인 '나이', '성별'도 전환의 원인이 됨
- 고객 소득, 사회적 배경, 나이와 같이 전환을 유도하나, 측정하지 않은(관측되지 않은) 변수 U
- 교차 판매 이메일이 무작위로 발송 → T를 가리키는 랜덤화 노드로 표현
※ 인과관계 그래프 DAG(Directed Acyclic Graph, 유향 비순환 그래프)
: 방향이 있는 부분은 '엣지'로 방향성을 나타내고, 비순환 부분은 그래프에 루프나 순환이 없음을 나타낸다. 인과관계의 되돌릴 수 없는 비가역적(nonreversible) 가정을 방향성 있는 비순환 그래프로 표현
# DAG
g_cross_sell = gr.Digraph()
g_cross_sell.edge("U", "conversion")
g_cross_sell.edge("U", "age")
g_cross_sell.edge("U", "gender")
g_cross_sell.edge("rnd", "cross_sell_email")
g_cross_sell.edge("cross_sell_email", "conversion")
g_cross_sell.edge("age", "conversion")
g_cross_sell.edge("gender", "conversion")
g_cross_sell
- 그래프의 각 노드는 확률변수
- 화살표/엣지를 사용하여 한 변수가 다른 변수의 원인이 되는지 표시
- 이메일은 전환의 원인이 되고, U가 나이/전환/성별의 원인임을 나타냄
→ 관측 가능한 변수(나이,성별)을 X 노드 1개로 묶어보자.
g_cross_sell = gr.Diagraph(graph_attr={"rankdir" : "LR"}) # LR로 설정하여 그래프가 왼쪽에서 오른쪽으로 화살표가 향하도록
g_cross_sell.edge("U", "conversion")
g_cross_sell.edge("U", "X")
g_cross_sell.edge("cross_sell_email", "conversion")
g_cross_sell.edge("X", "conversion")
g_cross_sell
- 흥미로운 점은 DAG에서 가장 중요한 정보는 그래프 안에 없을 수 있다는 사실
- '엣지'가 없다라는 건 두 변수 사이에 직접적인 인과관계가 없다고 가정하는 것 (ex. u와 이메일 발송)
3.1.2 컨설턴트 영입 여부 결정하기
: 컨설턴트 영입(X)이 회사의 수익(Y)에 영향을 줄까?

- 측정할 수 없는 다른 요소가 변수의 원인이 되기에 각 변수에 U(Unknown)노드를 추가함
- 그래프는 일반적으로 확률변수를 나타내기 때문에, 임의의 U가 모든 변수의 원인이 됨
- 하지만 이러한 요소(U)들은 인과에 직접적 영향을 주지 않기에 일단 생략

① 과거 수익(C) → 컨설턴트 고용(X)
: 회사가 잘 된다면 컨설턴트를 고용할 비싼 서비스 비용을 지불할 수 있지만, 과거 실적이 좋지 않다면 여유가 없을 것 (*이 관계는 결정적(determinate)이지 않으며, 단지 가능성이 더 높다는 의미)
② 과거 수익(C) → 이후 수익(Y)
: 지난 6개월 간 잘된 회사는 이후 6개월 수익도 좋을 가능성이 높다.
→ 컨설턴트 고용(X)과 이후 수익(Y) 사이 연관성에는 두 가지 연결(①,②)이 있어 정확한 인과관계를 구분하는 것이 어렵다.
3.2 그래프 모델 집중 훈련
그래프 모델에 어떤 (조건부) 독립성 가정이 수반되는지 이해하는 것이 중요하다. 세 가지 그래프 구조와 예시를 살펴보자
*편의 상 Treatment(처치)를 T가 아닌 X로 표현함
3.2.1 사슬(Chain) 구조
X와 Y사이에 '매개자(Mediate)'가 존재

- 운동을 많이 하면 면역력이 좋아지고, 면역력이 좋은 사람은 폐암이 걸릴 확률이 낮아진다.
- 운동을 많이하면 폐암이 걸릴 확률이 낮아질지 알 수 없지만, 매개자인 '면역력' 변수를 통해서 간접적으로 인과관계를 도출할 수 있음
✅ EX. 인과추론(X)을 잘하면 승진(Y)할 확률이 높아질까?

→ 인과추론 지식(X)은 문제 해결력(M)을 향상시키고, 이는결국 승진(Y)의 원인이 된다고 했을 때, 승진이 인과추론 지식과 연관되는 것과 마찬가지로 인과추론 지식도 승진과 연관된다.
→ 이렇게 두 변수가 서로 연관되면 독립이 아니다.
→ T는 M의 원인이 되고, M은 Y의 원인이 된다. 중간노드(M)은 T와 Y사이의관계를 매개하는 역할로, 매개자(mediate)라 한다.
→ 인과관계는 화살표 방향으로만 흐르지만, 연관관계는 양방향으로 흐르는 것이 특징
✅ Conditioning
: 그래프에서 변수 고정하기 (=변수를 조건부로 설정하기)
→ 특정 변수 값을 일정하게 유지하면서 다른 변수들 간의 관계를 관측하는 것, 이를 통해 해당 고정변수의 영향을 통제하여 다른 변수들 사이의 관계를 더 명확하게 이해할 수 있다.
Backdoor paths
: 같은 정보를 공유하면 두 노드는 연결되어 있다고 본다. 직/간접적인 인과관계가 아닌 연결(path)을 backdoor paths라 부른다. 이 모든 backdoor path를 차단하는 것이 인과관계를 찾아내는 일
→ 이 path를 차단하는 것 ↔ 변수를 고정하는 것 ↔ 변수를 조건부로 설정(=conditioning)하는 것
EX. X⊥Y|A에서 A가 conditioning되어 있고, 그 의미는 A로 통하는 information(=backdoor path)이 차단되었다는 것

✅ 사슬(Chain) 구조에서의 조건부

- X와 M이 정보를 공유하고, Y와 M이 정보를 공유하고 있으며, 이에 따라 X와 Y도 정보를 공유하고 있다.
- M과의 연결을 차단하면(conditioning하면) X와 Y는 공유하고있던 관계가 사라져 d-separated된다.
- 따라서 backdoor path가 존재하는 사슬 구조에서는, M을 조건부로 두어야한다.
✅ EX. 인과추론(X)을 잘하면 승진(Y)할 확률이 높아질까? 예제로 돌아가서,
문제 해결력을 조건부로 두어 backdoor paths를 차단하면,
(↔ 매개자인 문제 해결력을을 고정하여, M이 동일한 사람이라고 가정 )

- 종속성이 차단된다.
- 그래서 M이 주어졌을 때, T와 Y는 독립이 된다. (T⊥Y | M)
M(문제 해결력)에 대한 조건부가 무엇을 의미할까?
: 문제 해결력이 동일한 사람들을 살펴볼 때, 어떤 사람이 인과추론 지식(X)을 갖고 있는지 알아도, 승진 가능성(Y)에 대한 추가 정보는 얻을 수 없다.
- E[Y|M,X] = E[Y|M] <- M이 동일한 사람들 중 X의 유무 확인으로는 Y에 대한 추가 정보를 얻을 수 없다는 의미
- 반대로 승진 상태(Y)를 알아도 인과추론 지식(X)에 관한 추가 정보를 제공하지 않는다. (모든 backdoor path가 차단됨)
✅ EX. 기온(X) 상승은 도넛(Y) 매출에 영향을 미칠까?
[기온 X] ------> [아이스 커피 매출 M] ------> [도넛 매출 Y]
- 기온이 높아지면 아이스커피가 잘 팔린다.
- 아이스커피가 잘 팔리면, 도넛도 잘 팔린다.
- 기온이 높아져 아이스 커피 매출이 증가하고, 아이스 커피가 매진되었다면,(↔아이스 커피 매출이 없는, 고정된 조건부 상태)
- 아이스 커피의 재고가 생길 때 까지 기온의 변화(X)가 도넛 매출(Y)에 영향을 주지 않는다. ↔ X와 Y의 backdoor paths가 차단되어, X와 Y의 관계가 d-separated 된다.
M(아이스 커피) 매출로 기온(X)이 상승했지만, 도넛(Y)의 매출은 증가하지 않았을 때 어떻게 해석해야할까?
→ 화살표(매개자와의 인과관계)가 약해졌는지 확인하기
- X→M backdoor path 확인: 기온(X)이 상승했으나, 아이스 커피(M) 매출이 상승하지 않음 (외부 기온은 높으나 매장 내 온도가 낮아져 첫 번째 화살표가 약해진 경우)
- M→Y backdoor path 확인: 아이스 커피(M) 매출이 상승했으나, 도넛(Y) 매출이 상승하지 않음 (도넛 외에 다른 신제품이 나와서 두 번째 화살표가 약해진 경우)
3.2.2 분기(Fork) 구조
X와 Y에 '공통 원인(Common cause)'이 존재

- 운동(X)을 많이 하면 폐암(Y)에 걸릴 확률이 낮아질까? 운동과 폐암 모두 '흡연 여부'(C)라는 공통 원인이 존재한다.
- 운동(X)을 많이 하는 사람은 비흡연자(C)인 경우가 많기에, C→Y관계에 따라서 폐암(Y)이 걸릴 확률이 낮을 수 있을 것이다.
✅ EX. 인과추론(X)을 잘하면 머신러닝(Y)도 잘할 수 있을까?

인과추론(X)을 잘하기 위해서는 통계학(C)이 필요하고, 머신러닝(Y)을 잘하기 위해서도 통계학(C)이 필요하다.
→ A는 인과추론(X)을 잘 안다.
→ 따라서 A는 통계학(C)을 잘 알 가능성이 높기에, 머신러닝(Y)도 잘할 수 있을 것이다.
* 공통 원인은 교란 요인(confounder)이라고도 한다.
✅ 분기(Fork) 구조에서의 조건부

- X와 C가 정보를 공유하고, Y와 C가 정보를 공유하고 있으며, 이에 따라 X와 Y도 정보를 공유하고 있다.
- C와의 연결을 차단하면(conditioning하면) X와 Y는 공유하고 있던 관계가 사라져 d-separated된다.
- 따라서 backdoor path가 존재하는 분기 구조에서는, C를 조건부로 두어야 한다.
✅ EX. 문제해결력(X)이 좋은 지원자가 좋은 직원(Y)이 될까?
(↔분기 구조에서 공통 원인을 공유하는 두 변수는 종속이지만, 공통 원인이 주어지면 독립이 된다)
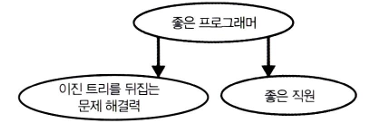
좋은 프로그래머(C)가 문제해결력을 통한 좋은 성과(X)를 내고,
좋은 프로그래머(C)가 좋은 직원(Y)일 확률이 높다고 가정했을 때,
1. 좋은 프로그래머(C)인지 모를 때
문제 해결력이 존재하는지 모르지만, 이진 트리를 뒤집는 문제 해결력을 판단할 수 있는 질문을 면접 질문으로 설정함으로써, 문제 해결력(X)이 존재한다면 좋은 프로그래머(C)임을 알 수 있고, 해당 지원자가 좋은 직원(Y)일 확률이 높다는 사실도 알 수 있다.
↔ C에 따라 달라지는 X와 Y의 인과관계
2. 좋은 프로그래머(C)임을 이미 알 때 (=C가 조건부로 고정되어 있을 때)
이 때에는 설정한 면접 질문(X)이 지원자가 좋은 직원(Y)이 될 것인지에 대한 추가 정보를 제공하지 않는다.
즉, 이진 트리를 뒤집는 문제해결력을 알 수 있는 면접 질문에 대답하는 것(X)과 좋은 직원(Y)이 되는 것은 독립이다.
↔ C가 고정되어 있을 경우 X와 Y는 독립이다.
3.2.3 충돌부(Collider) 구조
X와 Y에 공통의 효과가 존재


충돌부(Collide)
: 두 변수가 공유하는 공통의 효과를 가리킴 (두 개의 화살표가 충돌해서 충돌부라 부름)
- 충돌부 구조에서 두 부모 노드는 서로 독립(d-separated)이다.
- 하지만, 공통 효과를 조건부로 두면 (연관 경로가 열리면서) 부모 노드의 변수들은서로 종속(d-connected)이 된다.
✅ 충돌부(Collilder)에서의 조건부

- X와 Z가 정보를 공유하고, Y와 Z가 정보를 공유하고 있지만, X와 Y가 정보를 공유하고 있지 않기에 d-separated되어 있다. (↔ 사슬,분기구조)
- Z와의 연결을 차단하면(conditioning하면) X와 Y는 각각 Z와 공유하고 있던 정보가 뒤섞여 d-connected(종속)된다.
- 따라서 backdoor path가 이미 차단되어 있는 충돌부 구조에서는, Z를 조건부로 두어서는 안된다.
✅ EX. 공부(X)를 많이 하면 친구(Y)가 많지 않을까?
- 공부를 많이 하면 성공할 확률이 높다.
- 친구가 많으면 성공할 확률이 높다.
→ '성공'은 collider(공통 효과)

만약 collider(성공)을 차단한다면? (=조건부로 성공한 사람만 대상으로 x와 y의 관계를 본다면?)

✅ 공통 효과간의 tradeoff
한 가지 원인이 이미 효과를 설명하므로, 다른 원인의 가능성은 낮아진다. (↔ 다른 요인에 의해 설명되는 현상)
✅ EX. 통계 지식과 아부 사이에 인과관계가 있을까?
통계 지식(X)이 있거나, 아부(Y)하는 사람이 승진(Z, Collider)할 수 있다 했을 때
- 승진(Z)을 조건부로 하지 않는다면, 통계 지식(X)과 아부(Y)는 독립이다. 즉, 통계 지식(X) 이 있는 건 아부(Y) 관한 정보를 주지 않는다.
- 반면에, 승진(Z)했다면, (↔ 승진(Z)을 조건부로 한다면) 아부(Y)를 잘할 가능성이 높다.
- 통계 지식(X)을 갖고 있다면 승진(Y)을 할 가능성이 높기에, 아부(Y)는 잘 하지 못할 가능성이 높다.
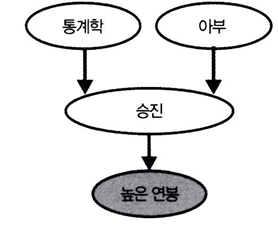
충돌부(Z,승진)를 조건으로 두지 않고 충돌부의 원인(X,Y)을 조건부로 해도, 충돌부 원인들은 종속된다.
즉, 승진 정보(Z)를 모르지만, 거액 연봉 정보(Z2)를 안다면, 통계 지식(X)과 아부(Y)는 종속적인 관계가 된다.
↔ 공통 효과(거액 연봉)를 공유하는 원인(통계학)이 다른 원인(아부)에 의해 설명되기 때문
↔ 하나(통계학)를 가지면 다른 하나(아부)를 가질 가능성이 낮아지기 때문
3.2.4 연관성 흐름 치트 시트
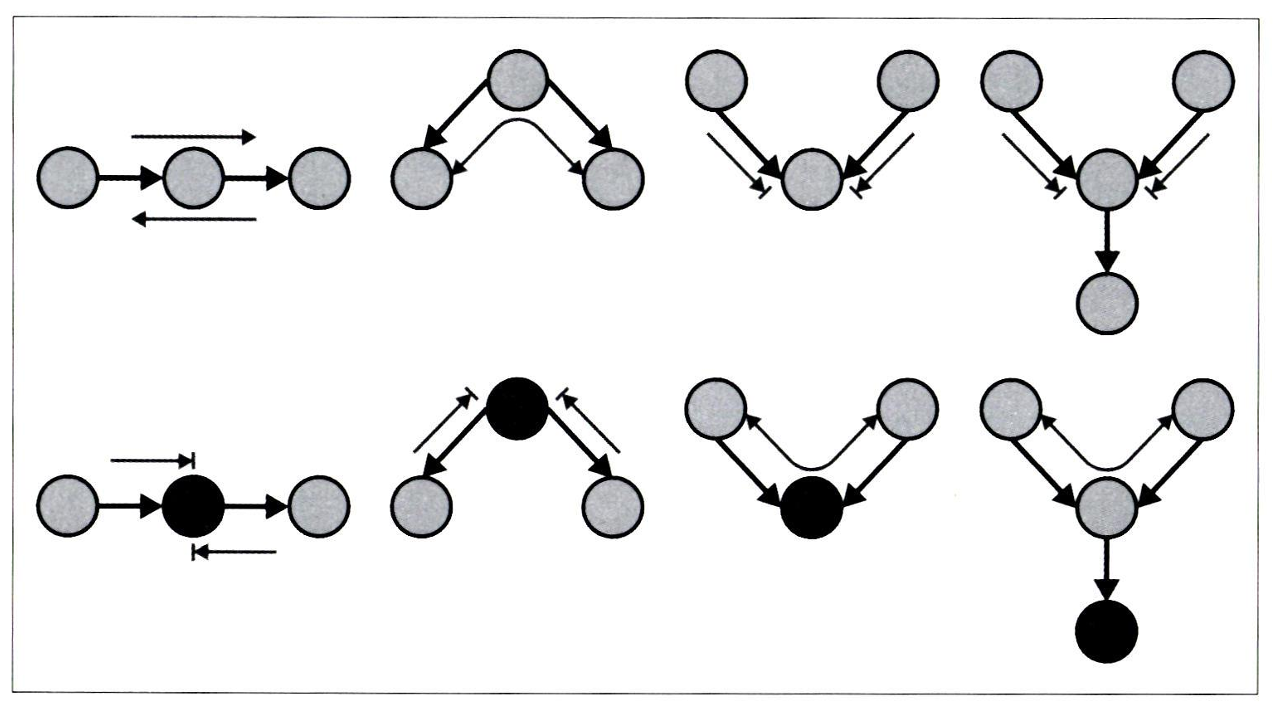
3.2.5 파이썬에서 그래프 쿼리하기

다음과 같은 질문에 답해보자.
- D와 C는 종속? (N, 공통 효과 A를 공유하는 D와 C는 충돌부 구조, 독립)
- A가 주어진 경우, D와 C는 종속? (Y, 공통 효과 A를 공유하는 D와C는 충돌부 구조, 조건부 하에서 종속)
- G가 주어진 경우, D와 C는 종속? (Y, 공통 효과 G의 충돌부A의 원인 D와 C는 종속관계)
- A와 B는 종속? (Y, C를 공통원인으로 갖는 A와 B는 분기 구조, 종속관계)
- C가 주어진 경우, A와 B는 종속? (N, 분기구조는 조건부 하에서 독립관계)
- G와 F는 종속? (N) → G와 E는 C를 공통 원인으로 둔 분기 구조, 하지만 충돌부 E에서 연관성이 멈춤
- E가 주어진 경우, G와 F는 종속? (Y) → E를 조건부로 두면 연관성이 충돌부로 흐르기 시작하고 경로가 열리면서 G와 F가 연결된다.
그래프 모델을 다루는 라이브러리인 networks 라이브러리의 Diagraph 함수에 넣어서 확인해보자.
import networkx as nx
model = nx.DiGraph([
("C", "A"),
("C", "B"),
("D", "A"),
("B", "E"),
("F", "E"),
("A", "G"),])
1,2,3번 = D와 C는 A를 충돌부로 둔 충돌부 구조
print("D와 c는 종속?")
print(not(nx.d_separated(model, {"D"}, {"C"}, {})))
> D와 c는 종속?
> False# A가 주어졌을 때 D와 C가 종속인지 확인
print("조건부 A하에서 D와 C는 종속?")
print(not(nx.d_separated(model, {"D"}, {"C"}, {"A"})))
> 조건부 A하에서 D와 C는 종속?
> True# G가 주어졌을 때 D와 C가 종속인지 확인
print("조건부 G하에서 D와 C는 종속?")
print(not(nx.d_separated(model, {"D"}, {"C"}, {"G"})))
> 조건부 G하에서 D와 C는 종속?
> True
4,5번 - D와 G는 연관성이 A를 통해서 연쇄적으로 흐르는 사슬 구조
print("G와 D는 종속?")
print(not(nx.d_separated(model, {"G"}, {"D"}, {})))
> G와 D는 종속?
> Trueprint("조건부 A하에서 G와 D는 종속?")
print(not(nx.d_separated(model, {"G"}, {"D"}, {"A"})))
> 조건부 A하에서 G와 D는 종속?
> False
6,7번 - 모든 것을 종합하여 G와 F를 보면, 분기(C)-충돌부(E) 구조
print("G와 F는 종속?")
print(not(nx.d_separated(model, {"G"}, {"F"}, {})))
> G와 F는 종속?
> Falseprint("조건부E하에서 G와 F는 종속?")
print(not(nx.d_separated(model, {"G"}, {"F"}, {"E"})))
> 조건부E하에서 G와 F는 종속?
> True
✅ 3.1.2 컨설턴트 영입 여부 결정하기 로 돌아가서,

새로 습득한 기술(인과 그래프 구조)을 통해서 연관관계가 인과관계가 아닌 이유를 확인할 수 있다.
이 그래프에서 컨설팅(X)과 이후 6개월 수익(Y)은 이전 6개월 수익(C)을 공통 원인으로 둔 분기 구조가 존재함
따라서 컨설팅(X)과 기업의 미래 실적(Y)사이에는 두 가지 흐름이 연관됨
- 직접적인 인과 경로
- 공통 원인(이전 6개월 수익)때문에 교란받는 비인과 경로(noncausal path=backdoor path, 뒷문 경로)
→ 2번 backdoor path가 있다는 의미는, X와 Y간의 관측된 연관관계를 인과관계로 볼 수 없음을 보여준다.
→ 그래프 내에서 연관성이 backdoor path로 어떻게 흐르는지 이해하면, 연관성과 인과성의 차이를 더 정확히 이해할 수 있다.
이제 그래프 모델이라는 새로운 관점에서 식별의 개념을 다시 살펴보자.
'데이터 분석 > 인과추론' 카테고리의 다른 글
| [4-2] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 (0) | 2024.05.12 |
|---|---|
| [4-1] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 (0) | 2024.05.09 |
| [3-2] 실무로 통하는 인과추론 with 파이썬 - 3장. 그래프 인과모델 (0) | 2024.05.05 |
| [2] 실무로 통하는 인과추론 with 파이썬 - 2장. 무작위 실험 및 기초 통계 리뷰 (0) | 2024.04.21 |
| [1] 실무로 통하는 인과추론 with 파이썬 - 1장. 인과추론 소개 (1) | 2024.04.14 |




