| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- lightgbm
- 데이터 핸들링
- splitlines
- tableau
- XGBoost
- 그룹 연산
- 3기가 마지막이라니..!
- sql
- pmdarima
- 마케팅 보다는 취준 강연 같다(?)
- 로그 변환
- WITH CUBE
- 스태킹 앙상블
- WITH ROLLUP
- 분석 패널
- ImageDateGenerator
- 컨브넷
- ARIMA
- Growth hacking
- 그로스 해킹
- 부트 스트래핑
- 데이터 증식
- 그로스 마케팅
- 캐글 신용카드 사기 검출
- 캐글 산탄데르 고객 만족 예측
- 인프런
- python
- DENSE_RANK()
- 리프 중심 트리 분할
- 데이터 정합성
- Today
- Total
LITTLE BY LITTLE
[2] 실무로 통하는 인과추론 with 파이썬 - 2장. 무작위 실험 및 기초 통계 리뷰 본문

목차
<2장. 무작위 실험 및 기초통계 리뷰>
2.1 무작위 배정으로 독립성 확보하기
2.2 A/B 테스트 사례
2.3 이상적인 실험
2.4 가장 위험한 수식
2.5 추정값의 표준오차
2.6 신뢰구간
2.7 가설검정
2.7.1 귀무가설
2.7.2 검정통계량
2.8 P값
2.9 검정력
2.10 표본 크기 계산
2.11 요약
2.1 무작위 배정으로 독립성 확보하기
: 독립성 가정을 만족하면 실험군과 대조군의 평균을 비교하여 간단히 ATE를 식별할 수 있다.
- (1장) 실험군과 대조군에서 처치 이외에 나머지 조건이 동일하다면(=편향이 없다면) 연관관계는 인과관계가 된다. (=적어도 실험군과 대조군의 잠재적 결과에 대한 기댓값이 같다)
- (1장) 잠재적 결과가 처치와 독립인 경우 연관관계와 인과관계가 동일해진다. 라는 말이, 처치와 결과 사이의 독립성을 이야기하는 것이 아니라는 점이 중요하다.
- 처치와 결과가 독립이라는 것은 처치가 관측하려는 결과에 아무런 영향을 미치지 않게 된다는 것
- 즉, 우리는 결과가 아니라 잠재적 결과가 처치와 독립적이기를 바란다.
- 우리가 처치가 어떻게 이루어졌는지 처치 배정(treatment assignment)에 관해 안다고 해도, 기준이 되는 잠재적 결과 Y0에 관한 정보는 얻을 수 없다. 따라서 (Y0, Y1) ⊥ T는 실험군-대조군 결과 차이를 유발한 요인이 바로 처치라는 것을 의미할 수 있게 됨
따라서 독립성을 만족시키기위해서 처치의 무작위 배정이 필요하다.
↔ 랜덤화는 처치와 잠재적 결과를 독립적으로 만든다.
2.2 A/B테스트 사례
무작위 배정이 되었는지 확인하기
(실험그룹이 유사한지 평가하기 [평균,표준오차] )
커피 프리미엄 구독 서비스
: 저렴한 기본 상품을 매주 배송해주는 저렴한 월간 구독서비스. 저가형 상품을 구독하는 사용자들에게 프리미엄 서비스를 판매하고 싶은 상황에서 프리미엄 상품 홍보 이메일이 얼마나 효과적인지 알아내야 한다.
랜덤화되지 않은 기존 데이터를 살펴보았을 때,
1. 이메일을 받은 고객이 프리미엄 구독을 구매할 가능성이 더 높다. (이메일을 받은 고객이 더 전환이 많이 됐다)

2. 알고보니 애초에 전환 가능성이 높다고 생각한 고객에게만 이메일을 보냈다.

3. 이런 상황에서 편향을 없애려면 이메일을 받은 고객과 받지 않은 고객을 비교 가능하도록 만들어야 한다.
4. 이메일을 고객에게 무작위로 보냈다고 가정하기 위해서, 전체 고객을 무작위로 샘플링하여 1명에게는 이메일을 보내지 않고, 1명에게는 프리미엄 구독을 간단히, 나머지 1명에게는 자세히 설명하는 이메일을 보냈다는 세 가지 유형으로 무작위 설정)

그룹별 평균 전환율을 계산해서 인과효과 추정하기
data.groupby(["cross_sell_email"]).mean()
→ 이메일을 받지 않은 그룹의 전환율은 4.2%, 긴 이메일을 받은 그룹은 5.5%, 짧은 이메일은 12.5%의 전환율을 보임
→ 여기서 ATE = E[Y|T=t] - E[Y|T=0]로, 긴 이메일을 받은 그룹은 1.3%p의 증가를, 짧은 이메일은 8.3%p의 증가를 보여줌
✅ 실험그룹이 비슷한지 평가하기
: 무작위 배정이 제대로 이루어졌는지 확인하려면 실험군-대조군의 특성이 균형을 이루는지 확인
- 위의 gender과 age가 실험그룹들 사이에서 비슷한지 확인해보면, 나이는 비슷하나 성별에 차이가 있는 것을 알 수 있음
- 남성의 비율이 그룹 short는 63%, long은 55%, no email에서는 54%로, 효과가 가장 크게 나타난 실험군인 short가 다른 그룹과 매우 달라 신뢰도가 떨어지는 결과라고 볼 수 있음
- 짧은 이메일을 받았을 때 효과가 큰 이유가 E[Y0|man] > E[Y0|woman] 떄문일 수도 있기 때문

cross_sell_email 유형에 따라 gender과 age의 평균과 분산을 계산
- 유형별 평균과 표준오차 계산
- 대조군(no_email)의 평균과 차이를 구하고
- 그 차이의 표준오차로 나누기
X = ["gender", "age"]
mu = data.groupby("cross_sell_email")[X].mean()
var = data.groupby("cross_sell_email")[X].var()
norm_diff = ((mu - mu.loc["no_email"])/np.sqrt((var + var.loc["no_email"])/2))
norm_diff
# StatsModels의 CompareMeans 클래스를 사용해서 Cohen's d를 계산해도 된다
→ 임계값을 0.5로 보았을 때, short 그룹은 성별 차이(0.184)가 크고, long 그룹은 나이 차이(0.221)가 큰 것으로 보인다.
→ 소규모 표본은 무작위로 배정해도 그룹 간 차이가 클 수 있으나, 대규모 표본에서는 이러한 차이가 사라지는 경향이 있음
2.3 이상적인 실험
- RCT는 많은 시간과 비용이 들거나 비윤리적일 수 있다. 또한, RCT로도 해결할 수 없는 선택편향적 상황도 있음
- 따라서 RCT(Randomsized Controlled Trials)를 벤치마크로 활용하는 것이 목표
- RCT는 실험 없이도 인과효과를 발견할 수 있는 방법에 대한 통찰을 준다.
2.4 가장 위험한 수식
추정값이 타당한지 확인하기 - '표준오차'와 '표본 크기'
데이터는 무한하지 않다. 인과추론의 두 단계 중 1단계인 '식별'에서는 RCT가 유용하지만, 2단계인 '추론'을 위해서는 실험의 표본크기가 커야 한다.
→ 그 이유에 대한 통계 개념 복습
1. (표준편차에 대한) 드무아브르의 공식

(참고)
- SE는 평균의 표준오차 / 시그마는 표준편차 / n은 표본 크기
- 표준오차: 표본평균 추정값의 변동 (따라서 표본의 크기가 커질 수록 작아짐)
- 표준편차: 표본의 각 관측값과 표본 평균과의 차이
✅ EX. 고등학교 시험 점수 데이터
df = pd.read_csv('./Downloads/enem_scores.csv')
df.sort_values(by="avg_score", ascending=False).head(10)
상위 1% (np.quantile(0.99) 이상)) 학교만 따로 떼어내서 box plot 그려보기
plot_data = (df
.assign(top_school = df["avg_score"] >= np.quantile(df["avg_score"], .99))
[["top_school", "number_of_students"]]
.query(f"number_of_students<{np.quantile(df['number_of_students'], .98)}")) # 이상치 제거
plt.figure(figsize=(8,4))
ax = sns.boxplot(x="top_school", y="number_of_students", data=plot_data)
plt.title("Number of Students of 1% Top Schools (Right)");
→ 규모가 작은 학교일 수록 학업 성취도가 높다.
→ 교사 한 명에게 배정되는 학생 수가 적을수록 각 학생을 집중관리할 수 있으니 직관적으로도 맞는 것처럼 보임
→ 그런데 사람들은 하위 1%의 학교를 들여다보지 않았다. 이 학교도 학생 수가 매우 적었음
학생 수와 평균 점수의 분포를 보기 위해 scatter plot 그려보기
q_99 = np.quantile(df["avg_score"], .99)
q_01 = np.quantile(df["avg_score"], .01)
plot_data = (df
.sample(10000)
.assign(Group = lambda d: np.select([(d["avg_score"] > q_99) | (d["avg_score"] < q_01)],
["Top and Bottom"], "Middle")))
plt.figure(figsize=(10,5))
sns.scatterplot(y="avg_score", x="number_of_students", data=plot_data.query("Group=='Middle'"), label="Middle")
ax = sns.scatterplot(y="avg_score", x="number_of_students", data=plot_data.query("Group!='Middle'"), color="0.7", label="Top and Bottom")
plt.title("ENEM Score by Number of Students in the School");
→ 학생 수가 증가함에 따라 평균 점수는 더 정확해진다.(=분산이 작아진다)
→ 학생 수가 매우 적은 학교(=표본이 작음)에서는 단순히 우연때문에 점수가 높거나 낮을 수 있음(↔ 반대로 규모가 큰 학교에서는 우연이 작용할 가능성이 적음)
→ 드무아브르의 공식은 이러한 데이터의 부정확성을 지적
→ 불확실성을 정량화하는 한 가지 방법은 추정값의 분산을 계산하는 것 (불확실성은 표본의 크기가 클 수록 줄어듦)
✅ 체계적 오차와 무작위 오차
1. 체계적 오차(systematic error)
: 모든 측정값에 동일한 방식으로 영향을 미치는 일관된 편향
- 체계적 오차는 모든 측정값을 추정하려는 값에서 벗어나는 방향으로 밀어넣음. 따라서 표본의 크기가 늘어나도 줄어들지 않는다.
2. 무작위 오차(random error)
: 우연히 생긴 예측 불가능한 변동
- 드무아브르의 공식에서 볼 수 있듯이 표본의 크기가 증가함에 따라 줄어듦
- 통계학은 무작위 오차에서 오는 불확실성을 다루는 과학이므로 이러한 오류에 속지 않는다. 통계로 불확실성을 보완할 수 있음
2.5 추정값의 표준오차
추정값이 타당한지 확인하기 - ‘표준오차'와 '표본 크기'
2.4절에서 짧은 이메일은 8%p 이상의 인상적인 효과를 보였고, 긴 이메일은 1.3%p 증가에 그쳐 더 작은 영향을 주었다.
→ 구한 효과가 우연에 따른 것이 아니라고 확신할 만큼 표본 크기가 충분한가?
→ 수학적으로 봤을 때 이 효과가 통계적으로 유의한가?
→ 이를 알아보기 위해 표준오차 SE를 추정하기
df2 = pd.read_csv('./Downloads/cross_sell_email.csv')
df2
short_email = df2.query("cross_sell_email=='short'")["conversion"] # query는 조건에 맞는 데이터를 추출하는 loc같은 함수
long_email = df2.query("cross_sell_email=='long'")["conversion"]
email = df2.query("cross_sell_email!='no_email'")["conversion"]
no_email = df2.query("cross_sell_email=='no_email'")["conversion"]
df2.groupby("cross_sell_email").size()
pandas의 sd메소드로 표준오차 구하기
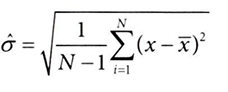
def se(y: pd.Series):
return y.std() / np.sqrt(len(y))
print("SE for Long Email:", se(long_email))
print("SE for Short Email:", se(short_email))
> SE for Long Email: 0.02194602460918551
> SE for Short Email: 0.030316953129541618
함수를 정의할 필요 없이 표준오차 계산 메소드 .sem() 활용하기 (sem, standard error of the mean)
print("SE for Long Email:", long_email.sem())
print("SE for Short Email:", short_email.sem())2.6 신뢰구간
추정값의 불확실성 반영하기(1) ‘신뢰구간’
표준오차
추정값의 표준오차 = 신뢰도를 나타내는 척도
- 통계학의 한 관점인 빈도주의 관점에서 데이터는 근본적인 데이터 생성 과정의 표현에 불과하다고 본다.
- 또한, 변하지 않는 값의 매개변수에 따라 정해지나, 그 참값은 알려지지 않음
- 교차 판매 이메일 예시에서 여러 번 실험하고 각각의 전환율을 계산해보면 정확히 같지는 않아도 근접할 수 있음
* 플라톤의 이데아론처럼(본질적 형태는 하나이나, 여러 행위 및 물체와의 결합 때문에 그 각각이 여럿으로 보임)
✅ 교차 판매 이메일 예시에서
- 실제 추상 분포를 안다고 가정, 전환은 0또는 1이므로 베르누이 분포를 따르며, 성공확률이 0.08이라 가정해보자
- 즉, 고객이 짧은 이메일을 받을 때마다 전환될 확률은 8%
- 실험을 10,000번 실행하고, 실험마다 100명의 고객 표본을 수집해서 짧은 이메일을 보내고 평균 전환율을 관측하여 총 10,000개의 전환율을 얻음
- 이 실험에서 얻은 10,000개의 전환율은 실제 평균인 0.08을 중심으로 분포할 것 (일부는 더 높고 일부는 더 낮겠지만, 추정된 평균은 실제 평균에 상당히 근접할 것)
*참고
: 리스트 컴프리헨션(=for문, 더 간결하고 가독성이 좋음)
[expression for item in iterable]
- expression: item에 대해 평가되는 식
- iterable: 반복 가능한 객체(리스트, 문자열, 튜플)
→ item을 사용하여 계산되며, 결과들이 새로운 리스트에 차례로 추가됨
# 리스트 컴프리헨션 - 시퀀스의 모든 항목에 함수를 적용하고 싶을 때 적용, for문과 효과가 같음
table_2 = []
for n in range(11): # range(11) = iterable
table_2.append(n*2) # n*2 = expression
table_2 = [n*2 for n in range(11)]
table_2
> [0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20]
실험에서 얻은 10,000개의 전환율이 실제 평균인 0.08을 중심으로 분포하는지 histogram을 그려 확인
n = 100
conv_rate = 0.08
def run_experiment():
return np.random.binomial(1, conv_rate, size=n)
np.random.seed(42)
experiments = [run_experiment().mean() for _ in range(10000)]plt.figure(figsize=(10,4))
freq, bins, img = plt.hist(experiments, bins=20, label="Experiment Means", color="0.6")
plt.vlines(conv_rate, ymin=0, ymax=freq.max(), linestyles="dashed", label="True Mean", color="0.3")
plt.legend()
- 실험의 평균값은 실제 이상적인 평균과 항상 일치한다고 볼 수는 없다. 하지만, 표준오차를 사용해 진행하는 실험의 95%에서 실제 평균을 포함하는 구간을 만들 수 있다.
- 현실에서는 여러 데이터셋에서 동일한 실험을 시뮬레이션 할 여유가 없고, 단 하나의 데이터셋만 있는 경우가 많음
- 여러 실험을 시뮬레이션하는 아이디어를 바탕으로 신뢰구간을 구성할 수 있다.
- 95%의 신뢰구간 = 실제 평균이 100번의 실험 중 95번은 신뢰구간 내에 속함을 의미
✅ CLT(Central Limit Theorem, 중심극한정리)
: 전환율 분포(0또는 1)는 베르누이 분포를 따르며, 히스토그램으로 그리면 성공률이 8%에 불과하므로 0에 긴 막대가 있고, 1에 짧은 막대가 있을 것

→ 데이터가 분포가 이처럼 정규분포가 아니더라도 데이터의 평균은 항상 정규분포를 따름
즉, 전환에 대한 데이터를 여러 번 수집하고, 매번 평균 전환율을 계산하면 이 평균들은 정규분포를 따르게 됨
이러한 사실을 통해서 정규분포 질량의 95%가 평균 위아래 표준편차 2배 내에 있다는 95% 신뢰구간을 계산할 수도 있음
✅ 교차 판매 실험으로 돌아가서, 유사한 실험을 여러 번 수행하면 전환율이 정규분포를 따르게 되기 때문에, 표준오차에 2를 곱하고 실험평균에서 더하고 빼면 실제 평균에 대한 95% 신뢰구간을 구할 수 있다.
exp_se = short_email.sem()
exp_mu = short_email.mean()
ci = (exp_mu - 2 * exp_se, exp_mu + 2 * exp_se)
print("95% CI for Short Email: ", ci)
> 95% CI for Short Email: (0.06436609374091676, 0.18563390625908324)x = np.linspace(exp_mu - 4*exp_se, exp_mu + 4*exp_se, 100)
y = stats.norm.pdf(x, exp_mu, exp_se)
plt.figure(figsize=(10,4))
plt.plot(x, y, lw=3)
plt.vlines(ci[1], ymin=0, ymax=4, ls="dotted")
plt.vlines(ci[0], ymin=0, ymax=4, ls="dotted", label="95% CI")
plt.xlabel("Conversion")
plt.legend()
좀더 보수적으로 99% 신뢰구간 찾기 (95%=1.96)
: scipy의 stats.norm.ppf - 표준정규분포의 누적분포함수(cumulative distribution function)의 역함수를 반환
ex. ppf(0.5) = 0.0 ↔ 표준정규분포의 질량 중 50%가 0.0미만에 위치한다.
from scipy import stats
z = np.abs(stats.norm.ppf((1-.99)/2))
print(z)
> 2.5758293035489004
ci = (exp_mu - z*exp_se, exp_mu + z*exp_se)
ci
> (0.04690870373460816, 0.20309129626539185)
→ short email 그룹의 평균 대한 95% 신뢰구간
long, no email 그룹의 평균 신뢰구간과 비교하기
def ci(y: pd.Series):
return (y.mean() - 2*y.sem(), y.mean() + 2*y.sem())
print("Short그룹의 95% 신뢰구간", ci(short_email))
print("Long그룹의 95% 신뢰구간", ci(long_email))
print("No email 그룹의 95% 신뢰구간", ci(no_email))
> Short그룹의 95% 신뢰구간 (0.06436609374091676, 0.18563390625908324)
> Long그룹의 95% 신뢰구간 (0.011153822341262012, 0.09893792077800405)
> No email 그룹의 95% 신뢰구간 (0.0006919679286838329, 0.08441441505003958)
→ 세 그룹의 신뢰구간이 서로 겹친다. ↔ 교차판매 이메일 발송이 전환율에 통계적으로 유의한 영향을 미친다고 할 수 없다.
→ 하지만 신뢰구간이 겹친다고 해서 그룹간 차이가 유의하지 않다고 단정할 수는 없음.
→ 요약하자면, 신뢰구간은 '추정값에 대해 불확실성을 나타내는 방법', 표본 크기가 작을 수록 표준오차가 커지고, 그 결과 신뢰구간도 넓어진다.
✅ EX. 코로나19 백신의 효과
- 30,420명의 지원자 중 백신과 위약을 1:1 비율로(15,210명씩) 무작위 배정
- 위약 참가자(T=0)중 185명 중 56.5명(95% 하에서 48.7~65.3)
- 백신 참가자(T=1)는 11명(95% 하에서 1.7~6.0)이 코로나 증상을 보임.
- → 백신 효능은 94.1%(95%하에서 89.3%~96.8%)
✅ 주의할 점
: 95% 신뢰구간이 95% 확률로 실제 평균을 포함한다고 말해서는 안된다.
- 특정 신뢰구간은 실제 평균을 포함할 수도, 포함하지 않을 수도 있다.
- 만약 포함한다면, 포함 확률은 95%가 아니고 100%이며, 그렇지 않은 경우 확률은 0%이다.
- 대신에 신뢰구간에서의 95%는 여러 차례 연구에서 계산된 신뢰구간이 실제 평균을 포함하는 '빈도'를 나타냄
- 하지만 실무에서는 신뢰구간이 95% 확률로 실제 평균을 포함한다고 해도 크게 문제될 것이 없다. 중요한 것은 추정값의 신뢰구간을 추가해야하는 것
2.7 가설 검정
추정값의 불확실성 반영하기(2) ‘가설 검정‘
> 불확실성을 반영하는 또 다른 방법은 '가설검정을 통해 결과를 제시하는 것'
가설검정 : 두 그룹 간의 평균 차이가 0(혹은 다른 특정 값)과 통계적으로 유의한 차이가 있는가?
- 질문에 대한 답을 하기 위해서는 두 독립 정규 분포의 합(차이) 역시 정규분포이어야 함
- 결과로 생성된 분포의 평균은 두 분포의 평균 합(차이)
- 결과로 생성된 분포의 분산은 두 분산의 합

import seaborn as sns
from matplotlib import pyplot as plt
np.random.seed(123)
n1 = np.random.normal(4,3,30000) # 정규분포를 가진 그룹1
n2 = np.random.normal(1,4,30000) # 정규분포를 가진 그룹2
n_diff = n2-n1
plt.figure(figsize=(10,4))
sns.distplot(n1, hist=False, label="$N(4,3^2)$")
sns.distplot(n2, hist=False, label = "$N(1,4^2)$")
sns.distplot(n_diff, hist=False, label=f"$N(-3, 5^2) = N(1,4^2) - (4,3^2)$")
plt.legend();
- 두 그룹을 빼서 만든 세 번째 분포의 평균은 두 분포 평균의 차이가 되고, 표준편차는 두 분산 합의 제곱근으로 계산됨
✅ 교차 판매 이메일 실험으로 돌아가서, 두 그룹(short, long)의 예상 분포를 가지고 한 그룹에서 다른 그룹을 빼면 그 차이의 분포를 얻을 수 있고, 분포를 통해 평균 차이(인과 효과)에 대한 95% 신뢰구간을 구할 수 있음
diff_mu = short_email.mean() - no_email.mean() # 두 평균의 차이
diff_se = np.sqrt(no_email.sem()**2 + short_email.sem()**2) # 두 분산 합의 제곱근
ci = (diff_mu - 1.96 * diff_se, diff_mu + 1.96 * diff_se)
print(f"short - no_email 그룹 인과효과의 95% 신뢰구간:\n{ci}")
> short - no_email 그룹 인과효과의 95% 신뢰구간: (0.010239808474398426, 0.15465380854687816)
2.7.1 귀무가설
추정값의 불확실성 반영하기(2) ‘가설 검정’
~ 추론 목적에 맞는 귀무가설 설정하기 ~
H0: short 그룹과 no_email 그룹의 전환율에 차이가 없다. (전환율이 같다.)
→ 앞서 구한 신뢰구간에는 0이 포함되어 있지 않기 때문에 전환율이 같지 않고, 유의수준 0.05 하에서 귀무가설을 기각할 수 있다.
→ short 그룹과 no_email 그룹간의 전환율에 차이가 없지 않다.
※ 유의수준 a
: 귀무가설이 참인데도 이를 기각하는 1종 오류를 범할 확률, 데이터 수집/ 분석 이전에 설정하기
만약 이메일 발송 비용이 과할 경우에만 이메일을 발송하지 않도록 하고 싶은 경우라면, 다른 귀무가설을 세울 수 있다.
H0: short 그룹과 no_email 그룹의 전환율 차이가 1%이다. (short그룹이 no_email 그룹보다 전환율이 1% 높다.)
→ 마케팅 팀은 전화율이 1% 이상 증가하는 경우에만 교차 판매 이메일을 발송할 수 있음
→ 이 가설을 검증하려면 평균 차이에서 1%를 빼서 신뢰구간을 이동하기만 하면 된다.
# 신뢰구간 이동
diff_mu_shifted = short_email.mean() - no_email.mean() - 0.01
diff_se = np.sqrt(no_email.sem()**2 + short_email.sem()**2)
ci = (diff_mu_shifted - 1.96 * diff_se, diff_mu_shifted + 1.96 * diff_se)
print(f"short - no_email 그룹 인과효과의 95% 신뢰구간:\n{ci}")
> short - no_email 그룹 인과효과의 95% 신뢰구간: (0.00023980847439843134, 0.14465380854687815)
→ 신뢰구간에 0이 포함되어있지 않기 때문에, short 그룹과 no_email 그룹의 전환율 차이가 1%라는 귀무가설을 기각할 수 있다.
→ short 그룹과 no_email 그룹의 전환에 1%의 차이가 없다.
차이를 2%로 변경시
# 전환율 차이가 2%일 때에는 0을 포함하여 귀무가설을 기각할 수 없다.
> short - no_email 그룹 인과효과의 95% 신뢰구간: (-0.009760191525601578, 0.13465380854687814)
→ 신뢰구간에 0이 포함되되어 있기 때문에 short 그룹과 no_email 그룹의 전환율 차이가 2%라는 귀무가설을 기각할 수 없다.
→ short 그룹과 no_email 그룹의 전환에 2%의 차이가 있다.(없지 않다)
✅ 비열등성 시험 (임상통계 개념)
: 신뢰구간에 0이 포함되는지 확인하는 동시에 신뢰구간이 충분히 작은지 확인하는 것
- 증거의 부재는 부재의 증거가 아니다.
- 단순히 표본 크기가 너무 작아 신뢰구간이 넓기 대문에 h0가 기각되지 않을 수 있다.
- 하지만 그것이 귀무가설이 참(차이가 없다)라는 뜻은 아님
- '차이가 없다'라기 보다는, "샘플 수가 작아서 차이가 있는지 발견하지 못했다"는 것이 정확한 결론
이 책에서는 대부분 귀무가설을 두 그룹이 동등하다(차이가 0이다)를 전제로 한다.
- 이렇게 귀무가설을 설정하는 의도는 효과가 0과 유의하게 다른 경우에만 처치를 하기 위함
- ex. 마케팅 캠페인을 중단하고자 할 때, 이 캠페인의 효과가 무시할 수 있을 정도로 작다면 캠페인을 중단해야할 것이고,
매개변수가 특정값과 다른 경우(차이가 있다)를 귀무가설로 세워야한다.
2.7.2 검정통계량
추정값의 불확실성 반영하기 (2) ‘가설 검정’
~ 귀무가설 기각 기준 값 ① 검정통계량 ~
- 신뢰구간 외에도 검정통계량을 사용하여 귀무가설을 기각하는 것이 유용할 수 있음
- 값이 클수록 귀무가설을 기각하는 방향으로 설정

- 분자 = 관측한 평균 차이와 귀무가설 사이에 대한 차이 (귀무가설이 참이면, 분자의 기댓값은 0이 됨
- 분모 = 표준오차로, 나눠주는 이유는 통계량의 분산이 1이되도록 정규화하기 위함
- 귀무가설이 참인 경우, t △~N(0,1) 표준정규분포를 따르게 됨
- 귀무가설 하에서 t △는 중심이기 때문에, 1.96보다 높거나, -1.96보다 낮은 값은 매우 드물게 나타남 (95%에서)
- 따라서 1.96보다 높거나, -1.96보다 낮은 t-통계량이 나타나면 귀무가설을 기각할 수 있다는 것
t_stat = (diff_mu - 0) / diff_se
t_stat
> 2.237951231871536
> 1.96보다 높기 때문에, 유의수준 0.05 하에서 귀무가설을 기각할 수 있다. (차이가 없지 않다) → 또한 t-통계량은 귀무가설 하에서 정규분포를 따르므로, p값을 쉽게 계산할 수 있음
✅ t-분포와 정규분포
: 정규분포 대신 표본 크기에서 추정하는 매개변수 수를 뺀 값인 자유도를 가진 t-분포를 사용해야 한다. (여기에서는 두 개의 평균을 비교하므로 n-2)
* 표본 크기가 충분히 큰 경우(ex.100)에는 t-분포와 정규분포 구분이 실질적으로 중요치않음
2.8 p 값
추정값의 불확실성 반영하기 (2) ‘가설 검정’
~ 귀무가설 기각 기준 값 ② p값 ~
- 앞서 short 그룹과 no_email 그룹의 전환율이 동일한데도 극단적인 차이가 날 확률은 5% 미만이라고 했다.(신뢰구간 95% 하에서 전환율에 차이가 없다는 충분한 근거가 없다.)
- 극단적인 차이가 날 확률 5% 미만을 정확하게 추정하기 위해 활용할 수 있는 것이 p 값
p값
: 귀무가설이 참이라고 가정할 때 관측된결과보다 더 극단적인 결과가 실제로 관측될 확률
- 관측한 값이 얼마나 이례적인지 측정
- P(data|H0)이다. ↔ P(H0|data)와 헷갈리지 말 것 (귀무가설이 참일 확률)

- 단측 귀무가설에서 p값은 표준정규분포에서 검정통계량 전에 해당하는 영역의 넓이를 계산하고,
- 양측 귀무가설은 해당 결과에 2를 곱하면 됨
p 값의 장점 중 하나는 95%, 99%와 같은 신뢰수준을 정할 필요가 없다는 것
✅ p값이 0.025인 경우
- 유의수준은 2.5%이다. 따라서 차이에 대한 95% 신뢰구간에는 0이 포함되지 않고(H0 기각), 99%에는 0이 포함(H0 기각 불가)될 것
- 차이가 실제로 0이라면 극단적인 검정통계량이 관측될 확률이 단 2.5%임을 나타냄
✅ EX. 대면 강의 vs 온라인 강의
: 주요연구 대학의 대규모 미시 경제학 입문 과정 수강생들을 무작위로 나눠 대면.녹화 강의에 배정하였다. 그 결과 대면 강의가 인터넷 강의보다 우세하다는 증거를 발견하였고, 히스패닉계 학생, 남학생, 성취도가 낮은 학생에게 특히 강하게 나타났다.
→ 무작위 배정을 사용해 실험군-대조군을 비교 가능하게 했으므로 내적 타당성이 있다고 할 수 있다.
→ 반면에 연구에 참여한 사람들은 무작위 표본이 아니라 미국 대학의 경제학 수강생이었으므로 결과를 다른 환경으로 일반화하는 외적 타당성은 없을 수 있다.
✅ 인과추론의 아킬레스건: 일반화 가능성 (외적 타당성)
*내적 타당성: 식별이 얼마나 타당하게 되었는가? (실험 설계/실행 과정에서 발생할 수 있는 외부 요인(ex.교란요인, 선택편향)의 영향을 효과적으로 제어하고, 인과효과를 정확하게 추론할 수 있는 구조가 마련되었다는 의미
*외적 타당성: 실험 결과가 다양한 상황,장소,시간,인구 집단에 일반화될 수 있는정도
인과추론은 내적 타당성을 추구하여 엄격하게 '통제'했기 때문에, 일반화하기 어렵다는 것이 인과추론의 가장 큰 약점
" 만약 실험 설계가 무작위하게 이루어지지 않았더라면 어떨지, 다른 환경에서 적용되어야 하는 경우를 염두에 두어야 하며,
인과추론 결과를 적용할 때, 적용하고자 하는 상황/맥락이 실험 조건과 얼마나 유사한지 질문을 던질 수 있어야 함 "
EX . 외국에서 최저임금이 고용률에 미치는 영향에 대한 연구결과를 우리나라에 적용할 때, 국가 특성의 차이를 고려해야 함
→ "표본"에 대한 이해가 중요
EX. 이웃과의 전기사용량 비교를 통한 전기 소비 감소를 유도하는 에너지 기업 Opower
→ 캘리포니아에서 일어난 실험 결과가 텍사스에서의 실험 결과와 같을까?
* Opower을 도입한 도시들이 무작위하게 선정된 게 아니고, 환경친화적인 고객이 많은 도시의 사업자들이 Opower를 일찍 도입하는 경향이 존재
* Opower을 초기에 도입한 도시의 특성과, 나중에 도입한 도시의 특성이 다르기 때문에 인과 효과가 정확하지 않을 수 있음
(환경에 대한 규제가 엄격한 도시로 캘리포니아가 있는데, 그래서 에너지 관련 연구가 캘리포티아에서 많이 시행되고 있는데, 이곳에서 나타난 인과효과는 매우 클 것이고,
반대로 친환경적인 의식이 적은 텍사스에서는 효과가 없을 것이라 예상하여 나중에 도입이 됐을 것이고 (역 인과관계 존재) 효과가 매우 작을 것)
→ 캘리포니아와 텍사스 각각 내에서는 내적 타당성이 잘 확보되었지만, 두 도시의 표본 특성이 다르기 때문에 두 실험 결과를 적용하는 데에는 주의해야 한다.
2.9 검정력
실험에 필요한 표본 크기 파악하기
(+비즈니스에 유의미할 효과 크기 설정하기)
데이터는 주어졌으나, 실험을 새로 설계해야하는 경우, 각 변수에 어떤 표본을 사용할지 결정해야 한다.
ex. 교차 판매 이메일을 보낼 고객 수를 어떻게 long, short, no_email로 나눌지 결정해야 한다면, H0를 기각할 경우 정확히 기각할 만큼 충분히 큰 표본을 확보하는 것이 목표
검정력(power)
: 귀무가설을 올바르게 기각할 확률
- 실험에 필요한 표본 크기를 파악할 때
- 제대로 실행하지 않은 실험에서 문제를 발견할 때 유용하다.
- a가 실제로 참인 귀무가설을 잘못 기각할 확률을 나타내는 반면, 검정력 (1- β)는 귀무가설이 거짓인 경우 이를 올바르게 기각할 확률로, 올바르게 기각하기 위해 필요한 증거의 충분성을 결정하기 위함
- β는 귀무가설이 거짓일 때 기각하지 않을 확률 (거짓 음성)
- 검정력의 일반적인 기준은 80%(↔귀무가설이 실제로 거짓임에도 불구하고 기각하지 않을 확률이 20%이다.)
- 즉, 80%의 검정력을 달성하려면, 귀무가설이 거짓일 때 80%의 확률로 귀무가설을 기각해야 함
- ↔ δ-1.96*SE > 0으로, 유의한 차이가 전체 실험의 80%에서 나타나야 하는 것
- ↔ 95% 신뢰구간의 하한이 0보다 높은 경우가 전체 실험의 80%에 달해야 하는 것

- 95% 신뢰구간의 하한은 정규분포를 따른다. 표준오차와 같은 분산을 가지며, 평균은 δ-1.96*SE
- 단지 표본평균의 분포를 1.96*SE만큼 이동한 것에 불과함
- 따라서 δ-1.96*SE > 0인 경우가 80%가 되려면(검정력 80%), 차이가 0에서 1.96*SE + 0.84*SE만큼 떨어져야 함
① 1.96은 95% 신뢰구간을 확보하기 위한 값
= 100번의 실험 중 95번 추정값이 유의미한 평균값에 속한다.
② 검정력에 해당하는 0.84는 신뢰구간의 하한이 0을 초과하는 경우가 전체의 80%에 해당하도록 하기 위한 값
= 100번의 실험 중 80번 귀무가설을 기각( δ =0이 아니다↔ 효과가 있다)할 수 있을 때 인과효과가 있다고 판단한다.
stats.norm.cdf(0.84)
> 0.7995458067395503
✅ 검정력 분석 (power analysis)
: 영향 주는 4가지 인자 중 3가지 인자가 결정되었을 때 나머지 변수 하나의 값을 구하는 분석
- 통계적 검정력 (ex. 80%) - 100번 실험 중 몇 번 효과가 있는 값인지 (몇 번 δ=0을 기각할 수 있는가?)
- 표본 크기
- 유의 수준 - 몇%의 추정값이 유의미한 평균에 속하지 않는가?
- 효과 크기(Minimum Detectable Effect) - 비즈니스적으로 효과가 있다고 간주하려면 두 집단이 최소한 어느 정도 차이가 나야하는가?
→ '효과 크기'의 중요성: 통계적으로 유의하더라도, 실제 비즈니스에서의 효과가 없으면 무의미하다.
- 인과 효과가 1%이고, 비즈니스에서1 %의 효과가 실제 액션을 취하는 데 있어서 무의미하다면, 그 1%가 통계적으로 유의한지 검정할 필요도 없을 것
- 실제 A/B 테스트 샘플 사이즈 계산기 (A/B테스트를 하는 데 몇 개의 표본이 필요한지 알려주는 계산기, ex. Optimizely)에서는
- 1. Baseline Conversion Rate(예상되는 실험군의 전환율, ex.3%)와
- 2. Minimum Detectable Effect(비즈니스에서 유의미한 실험군과 대조군의 전환율 최소 차이, 즉 인과추정량, ex. 20%),
- 그리고 3. 유의수준을 설정하면, 필요한 표본 크기(ex.13,000개)를 알려준다.
→ 비즈니스에서의 효과 크기를 설정해야 하는 이유는, 시간과 비용을 투입할 가치가 있는 실험을 하기 위해서이다.
(출처)
https://chaehwan-oh.github.io/experiment/2021/12/26/sample-size-calculator-statistics/
2.10 표본 크기 계산
귀무가설이 거짓일 때, 귀무가설과 관측된 추정값의 차이인 델타( δ
)를 감지할 수 있어야 한다.ex.a = 5%, 1- β = 80%라면, 감지 가능한 효과는 2.8*SE = 1.96*SE + 0.84*SE이다.↔ 이메일 예시에서 8% 전환율 차이를 감지하고자하는 교차 판매 이메일 실험을 설계하고자 한다면, 적어도 8%(↔2.8*SE)를 감지할 표본 크기를 확보해야 한다.
차이에 대한 표준오차 SE △ 공식에서

실험-대조군의 분산이 같을 것이라 가정할 때,
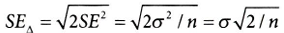
이 공식을 통해서 80% 검정력과 95% 신뢰도를 원할 때 표본 크기n을 결정하는 간단한 공식을 얻을 수 있다.

이 공식을 데이터에 적용하여 대조군의 분산을 시그마 제곱에 대한 가장 타당한 추정값으로 사용해서 필요한 표본의 크기를 정하면,
np.ceil(16 * (no_email.std() / 0.08) ** 2)
> 103.0df2.groupby("cross_sell_email").size()
> cross_sell_email
> long 109
> no_email 94
> short 120
> dtype: int64
→ 필요한 표본의 크기는 103, 우리의 실험에서는 두 실험군 모두 표본이 100개 이상이며, 대조군은 94개 표본을 확보했으므로 실험이 적절하게 진행되었음을 나타냄
2.11 요약
- 인과 추정량을 구하기 위한 첫 번째 단계인 '식별'에서, 1. 몇 가지 가정을 사용하여 2. 관측불가능한 인과 추정량을 추정할 수 있는 관측 가능한 통계량으로 바꿀 수 있다.
ATE = E[Y1-Y0]
- 식별에 필요한 가정 - 독립성 가정 T ⊥(Y0,Y1)
- 관측 가능한 E[Y|T=0]과 E[Y|T=1]을 사용해 ATE를 계산
1-1. 무작위 통제 실험을 활용하여 이 가정을 더 타당하게 만듦 (처치를 무작위로 배정하여 T가 잠재적 결과Yt와 독립이 되도록)
2-1. 관측 가능한 통계량으로 바꾸기 위해 표준오차 SE 사용

2-2. SE 공식을 통해 추정값 μ를 중심으로 신뢰구간을 구성
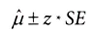
2-3. 두 그룹 간 평균 차이에 대한 신뢰구간을 구함 (두 그룹의 분산을 더하고, 그 차이에 대한 표준오차를 찾음)

2-4. 마지막으로 검정력과 이를 이용해 실험에 필요한 표본 크기를 계산 (95%신뢰도와 80% 검정력일 때)

기타 이것저것
A.평균처치효과와 조건부 평균처치효과
우리가 추론하는 건 언제나 "실험 집단에 대한 조건부 평균처치효과"이다.
이 조건부 평균처치효과가 어떻게 평균처치효과가 될 수 있는가?
→ ATET(Average Treatment Effect On Treated) = ATEC(Average Treatment Effect On Controlled) 가 될 때
B.내생성 (Endogeneity, 내부에서 생기거나 자라남) 3가지 유형
Y = α + βX + ε 에서 오차항(ε)과 연관되어 있는 변수를 의미함
1. 생략 변수(Omitted Variable, 선택 편향): 제 3의 요인이 X, Y 모두에 영향을 미치는 경우. X와 Y모두 연관된 생략 변수가 내생성을 유발 →
2. 동시성 편향(Simultaneity bias): X, Y가 서로 영향을 미치는 경우 (X↔Y가 아니라 X→Y이어야 함)
3. 측정오류: X뿐만 아니라 X에서 어떤 오차범위를 갖는 X'도 Y에 영향을 미치는 경우

C.내생성 해결 방법(1) 도구 변수 사용
방법1. 도구변수 사용
: x와 u(내생변수)의 고리를 끊는 도구
- 2번의 OLS를 거치면 된다.
① 독립변수 X에 영향을 미치는 도구 변수 Z를 찾아서 X를 회귀하는 회귀식을 만들고,
② 이를 이용해 추정된 X^을 이용하여 다시 Y를 추정하는 회귀식을 만드는 방법
- 도구변수의 조건은
X,Y에 영향을 미치는 내생변수 u가 있을 때,
1. u에 대한 상관성은 낮으면서,
2. X에 대한 상관성이 높은 새로운 변수
ex1. z = 대학까지의 거리, u = 대학 진학 여부
교육년수 → 임금 간의 인과관계 추정을 위해서 도구 변수로 '학생들의 집에서 대학까지의 거리'를 사용
1. u에 대한 상관성 ↓: 대학까지의 거리와 학생의 장래 임금 수준의 상관성은 매 낮다.
2. X에 대한 상관성 ↑: 집의 거리는 대학 진학과 상관성을 지닌다.
ex2. z = TV보유 여부, u = 학력
TV 시청 시간 → 성적 인과관계 추정을 위해서 도구 변수로 'TV 보유 여부'를 사용
1.u에 대한 상관성 ↓:TV 보유 여부가 아이들의 학력에 차별적인 영향을 주었을 가능성은 높지 않다.
2.X에 대한 상관성 ↑:TV 보유 여부는 티비 방송시간과 높은 상관성이 존재할 것이다.
* 해당 기간은 방송국의 신규 면허가 동결되어 TV방송국이 개국되지 못한 지역에 거주한 사람들은 TV를 볼 수 없어 TV 구매를 미뤘다.
한계점: 효율성이 떨어지고 신뢰구간이 넓어져 편향을 일으킬 수 있음
D.내생성 해결 방법(2) 효과 차분
방법2. 효과 차분
: 내생성이 시간의 흐름에 관계 없이 고정되어 있다면 DID모델을 사용할 수 있음
- 첫 번째 시점 before에서 두 번째 시점 after 값을 빼면 내생 변수가 사라짐.
한계점: 선택 편향은 제거하지 못하며 고정 변수가 아닌 내생성은 제거할 수 없다는 한계점이 있음
인과추론의 데이터과학
Part 3. 인과관계를 이해하는 분석틀 (3)
https://youtu.be/yS-N4YfZg0s?si=Vq5A0xA2Ok2f6d0z
'데이터 분석 > 인과추론' 카테고리의 다른 글
| [4-2] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 (0) | 2024.05.12 |
|---|---|
| [4-1] 실무로 통하는 인과추론 with 파이썬 - 4장. 유용한 선형회귀 (0) | 2024.05.09 |
| [3-2] 실무로 통하는 인과추론 with 파이썬 - 3장. 그래프 인과모델 (0) | 2024.05.05 |
| [3-1] 실무로 통하는 인과추론 with 파이썬 - 3장. 그래프 인과모델 (0) | 2024.05.01 |
| [1] 실무로 통하는 인과추론 with 파이썬 - 1장. 인과추론 소개 (1) | 2024.04.14 |




