| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- ImageDateGenerator
- 그로스 해킹
- python
- 3기가 마지막이라니..!
- 리프 중심 트리 분할
- lightgbm
- 스태킹 앙상블
- 컨브넷
- 그룹 연산
- 데이터 핸들링
- tableau
- 인프런
- WITH CUBE
- XGBoost
- 데이터 증식
- 데이터 정합성
- 부트 스트래핑
- WITH ROLLUP
- 그로스 마케팅
- 캐글 산탄데르 고객 만족 예측
- 마케팅 보다는 취준 강연 같다(?)
- sql
- ARIMA
- 분석 패널
- DENSE_RANK()
- pmdarima
- 로그 변환
- 캐글 신용카드 사기 검출
- Growth hacking
- splitlines
- Today
- Total
LITTLE BY LITTLE
[3] ARIMA - 직관적인 정상성 검정 방법 ACF/PACF Plot, 차분 본문

※ Review
1.
시계열 분석 모델 [단변량], hyper parameter p,d,q
2.
정상성의 개념, 정상성 검증 방법 ADF, KPSS Test
*ADF, KPSS Test = 단위근 테스트= 차분이 필요한지 객관적으로 결정하는 일반적인 방법
[3] 직관적인 정상성 검정 방법 ACF/PACF Plot, 차분
단순히 시계열 그래프만 보고나서 p,q값이 데이터에 맞았는지 이야기하기는 어렵다. 따라서 필수는 아니지만, ACF, PACF Plot을 참고할 필요성이 있다.
1. ACF (AucoCorrelation Function)와 PACF(Particlal ACF) 의 개념
: 현재의 값이 과거의 값과 어떤 관계를 갖고 있는지 보여주는 Plot
ACF
: 자기상관함수로, k시간 단위로 구분된 시계열의 관측치 간 상관계수 함수, k가 커질 수록 ACF는 0에 가까워
짐
- 과거의 값이 현재의 값에 준 영향만을 고려한 것이 PACF
- 과거의 값이 현재의 값에 도달하기 전까지 끼친 모든 간접적인 영향까지 모두 고려한 것이 ACF
PACF
: 부분자기상관함수로, 시차 k에서의 k단계만큼 떨어져 있는 모든 데이터 점들간의 순수한 상관 관계
- 부분상관이란 두 확률 변수 X와 Y에 의해 다른 모든 변수들에 나타난 상관 관계를 설명하고 난 이후에도 여전히 남아있는 상관관계를 의미함.
- 과거의 값이 현재의 값에 준 영향만을 고려한 것이 PACF
→ 시계열 분석에서의 목적
- 보다 직관적으로 정상성 만족 여부를 확인
- ARIMA(AR, MA, ARMA) 모델의 hyper parameter인 p,q를 결정할 때 사용
예제
1. 시계열 데이터 모양 확인
from scalecast.Forecaster import Forecaster
import matplotlib.pyplot as plt
import pandas_datareader as pdrf = Forecaster(y=data['death'], current_dates=data['date'])
f.plot()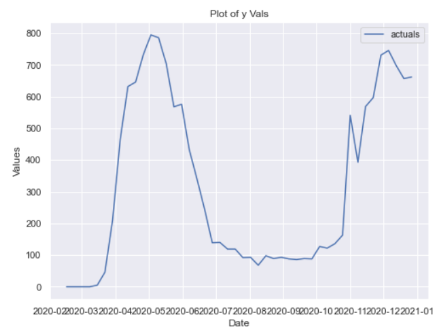
2. ACF, PACF Plot 그리기
f.plot_acf()
f.plot_pacf()
plt.show()
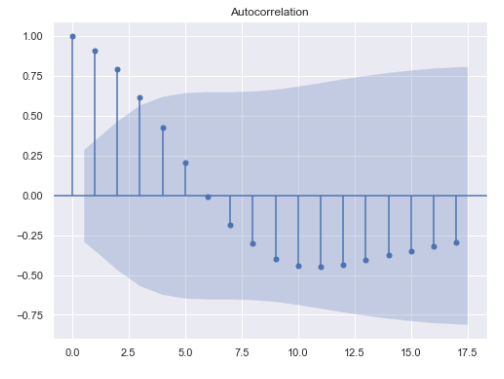
- y축의 값은 ACF의 값을 수치화 한 것
- x축의 값은 몇 개 이전의 값인지 lag 수를 의미 (0.0 = 현재의 값)
- 실핀처럼 생긴 막대가 파란색 상자 안에 들어가게 되면 통계적으로 값이 유의하지 않음

- x와 y축 값은 ACF와 동일함
- 여기에서도 파란색 상자 안에 막대가 들어가게 되면서부터 값이 유의하지 않음
| AR(p) 모델 적합 | MA(q) 모델 적합 | ARMA(p,q) 모델 적합 | |
| ACF Plot | 점점 작아지는 모습 | 첫 값으로부터 q개 뒤 끊기는 모습 (급격히 감소) |
점점 작아지는 모습 |
| PACF Plot | 첫 값으로부터 p개 뒤 끊기는 모습 (급격히 감소) |
점점 작아지는 모습 | 점점 작아지는 모습 |
3. 결과 해석
→ 위 결과에서 ACF Plot은 점점 작아지고, PACF Plot은 첫 값으로부터 1(=p)개 뒤에 끊기기 때문에, 이 데이터셋을 사용할 때에는 AR(1) 모델을 활용하는 것이 가장 정확도가 높을 것
ndiffs
:정상성 해결을 위한 차분 횟수를 결정할 수 있는 함수
Shift
: 특정 단위로 정보를 이동시킬 때 사용
diff
: 특정 시점 데이터와의 차이를 구할 때 사용
* 이 차분을 시각화했을 때 패턴이 잘 나타나는 경우도 있음
1. 적절한 차수 확인 (ndiffs)
from pmdarima.arima import ndiffs
import pmdarima as pm
kpss_diffs = ndiffs(y_train, alpha=0.05, test='kpss', max_d=6)
adf_diffs = ndiffs(y_train, alpha=0.05, test='adf', max_d=6)
n_diffs = max(adf_diffs, kpss_diffs)
print(f"차수 d = {n_diffs}")
>>>차수 d = 1
2. 차수 확인 후 1차 차분, 차분한 데이터의 정상성을 재확인 (ADF, KPSS Test)
: shift 함수를 사용하여 t기의 데이터를 t-1기로 밀어냄
diff = data['death'] - data['death'].shift()
result = adfuller(diff[1:])
→ result의 ADF Stats, P-value, Critical Values를 출력하여 p-value가 0.05보다 작기 때문에 귀무가설을 기각하여 정상성을 만족함을 확인
'데이터 분석 > 시계열 데이터 분석' 카테고리의 다른 글
| [5] ARIMA - auto_arima를 활용한 예제 실습 (0) | 2023.12.11 |
|---|---|
| [4] ARIMA - 시계열 모형 추가 설명 / 정상성 검정 정리 (0) | 2023.11.29 |
| [1] 시계열 군집 분석 - 계층적 군집화의 개념과 종류 (1) | 2023.11.24 |
| [2] ARIMA - 시계열 데이터, 정상성, 검정 방법(ADF/KPSS) (0) | 2023.11.11 |
| [1] ARIMA - 시계열 모델의 개념 (0) | 2023.11.08 |




